Trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Phần 2) có đáp án
Trắc nghiệm Toán 10 Cánh diều Bài 2. Biểu thức tọa độ của các phép toán vectơ (Phần 2) có đáp án (Vận dụng)
-
838 lượt thi
-
5 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trọng tâm G(23;0), biết M(1; –1) là trung điểm của cạnh BC. Tọa độ đỉnh A là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta có M là trung điểm của cạnh BC.
Suy ra {xM=xB+xC2yM=yB+yC2
Do đó {1=xB+xC2−1=yB+yC2
Vì vậy {2=xB+xC−2=yB+yC
Ta có G là trọng tâm của tam giác ABC.
Suy ra {xG=xA+xB+xC3yG=yA+yB+yC3
Do đó {23=xA+xB+xC30=yA+yB+yC3
Vì vậy {2=xA+xB+xC0=yA+yB+yC
Thế xB + xC = 2 vào xA + xB + xC = 2, ta được: xA + 2 = 2.
Suy ra xA = 0.
Thế yB + yC = –2 vào yA + yB + yC = 0, ta được: yA – 2 = 0.
Suy ra yA = 2.
Do đó tọa độ A(0; 2).
Vậy ta chọn phương án D.
Câu 2:
19/07/2024Trong mặt phẳng tọa độ Oxy, cho A(3; 3), B(–1; –9), C(5; –1). Gọi I là trung điểm của AB. Tọa độ M thỏa mãn →AM=−12→CI là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có I là trung điểm của AB.
Suy ra {xI=xA+xB2=3−12=1yI=yA+yB2=3−92=−3
Do đó tọa độ I(1; –3).
Vì vậy →CI=(−4;−2).
Suy ra −12→CI=(−12.(−4);−12.(−2))=(2;1).
Gọi M(xM; yM). Suy ra →AM=(xM−3;yM−3).
Ta có →AM=−12→CI.
Suy ra {xM−3=2yM−3=1
Do đó {xM=5yM=4
Vì vậy M(5; 4).
Vậy ta chọn phương án A.
Câu 3:
20/07/2024Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(3; 4), B(2; 1), C(–1; –2). Cho M(x; y) trên đoạn thẳng BC sao cho SABC = 4SABM. Khi đó x2 – y2 bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
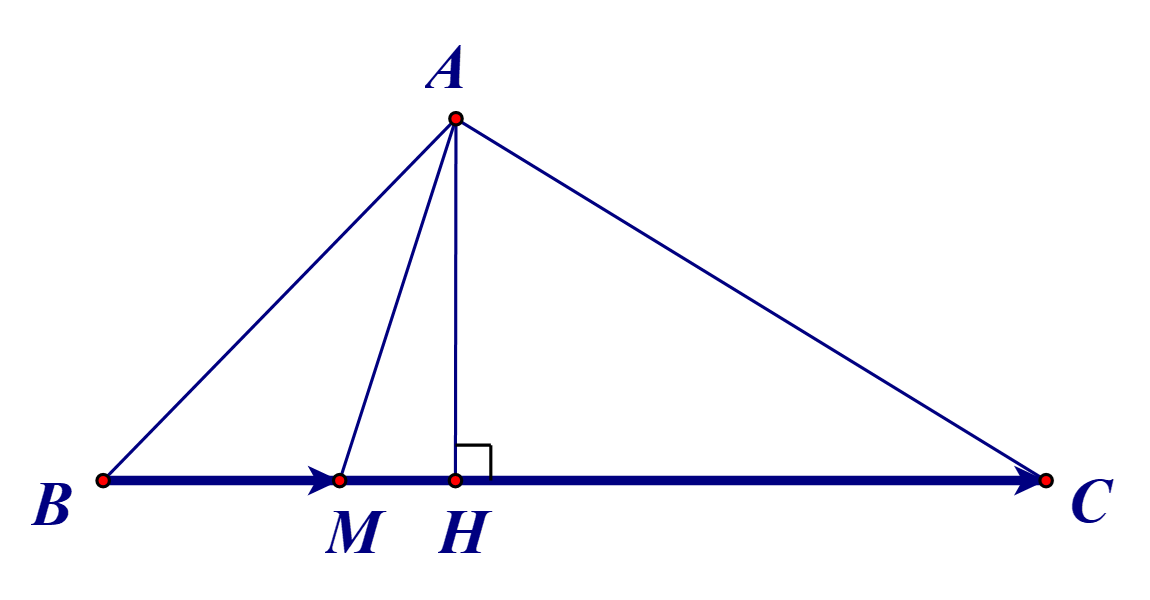
Kẻ AH ⊥ BC tại H.
Ta có:
⦁ →BC=(−3;−3). Suy ra 14→BC=(14.(−3);14.(−3))=(−34;−34);
⦁ →BM=(x−2;y−1).
Ta có SABC = 4SABM
Suy ra 12AH.BC=4.12AH.BM
Do đó BC = 4BM
Vì vậy BM=14BC
Suy ra →BM=14→BC
Do đó {x−2=−34y−1=−34
Vì vậy {x=54y=14
Suy ra x2−y2=(54)2+(14)2=138.
Vậy ta chọn phương án A.
Câu 4:
22/07/2024 Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có →AB=(4;4),→AE=(a+1;b+2).
Vì E di động trên đường thẳng AB nên ba điểm A, E, B thẳng hàng.
Tức là, →AE=k→AB
Suy ra {a+1=4kb+2=4k
Do đó a + 1 = b + 2
Vì vậy a = b + 1.
Khi đó tọa độ E(b + 1; b).
Ta có:
⦁ →EA=(−2−b;−2−b).
Suy ra 2→EA=(2(−2−b);2(−2−b))=(−4−2b;−4−2b);
⦁ →EB=(2−b;2−b).
Suy ra 3→EB=(3(2−b);3(2−b))=(6−3b;6−3b);
⦁ →EC=(3−b;−1−b).
Suy ra,
2→EA+3→EB−→EC=(−4−2b+6−3b−3+b;−4−2b+6−3b+1+b)=(−4b−1;−4b+3).
Khi đó |2→EA+3→EB−→EC|=√(−4b−1)2+(−4b+3)2
=√16b2+8b+1+16b2−24b+9=√2(16b2−8b+1)+8
=√2(4b−1)2+8.
Ta có (4b – 1)2 ≥ 0, ∀b ∈ ℝ.
Suy ra 2(4b – 1)2 ≥ 0, ∀b ∈ ℝ.
Khi đó 2(4b – 1)2 + 8 ≥ 8, ∀b ∈ ℝ.
Vì vậy √2(4b−1)2+8≥√8=2√2,∀b∈R.
Dấu “=” xảy ra khi và chỉ khi 4b−1=0⇔b=14.
Vậy |2→EA+3→EB−→EC| đạt giá trị nhỏ nhất khi và chỉ khi b=14.
Với b=14, ta có a=b+1=14+1=54.
Vậy ab=54.14=516.
Do đó ta chọn phương án C.
Câu 5:
18/07/2024Cho hai lực F1, F2. Biết →F1 và →F2 có cùng cường độ lực là 100 N, góc hợp bởi →F1 và →F2 là 120°. Khi đó cường độ lực tổng hợp của →F1 và →F2 bằng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Gọi →F là lực tổng hợp của →F1 và →F2.
Chọn hệ tọa độ Oxy như hình vẽ, với x và y được tính bằng đơn vị Newton.
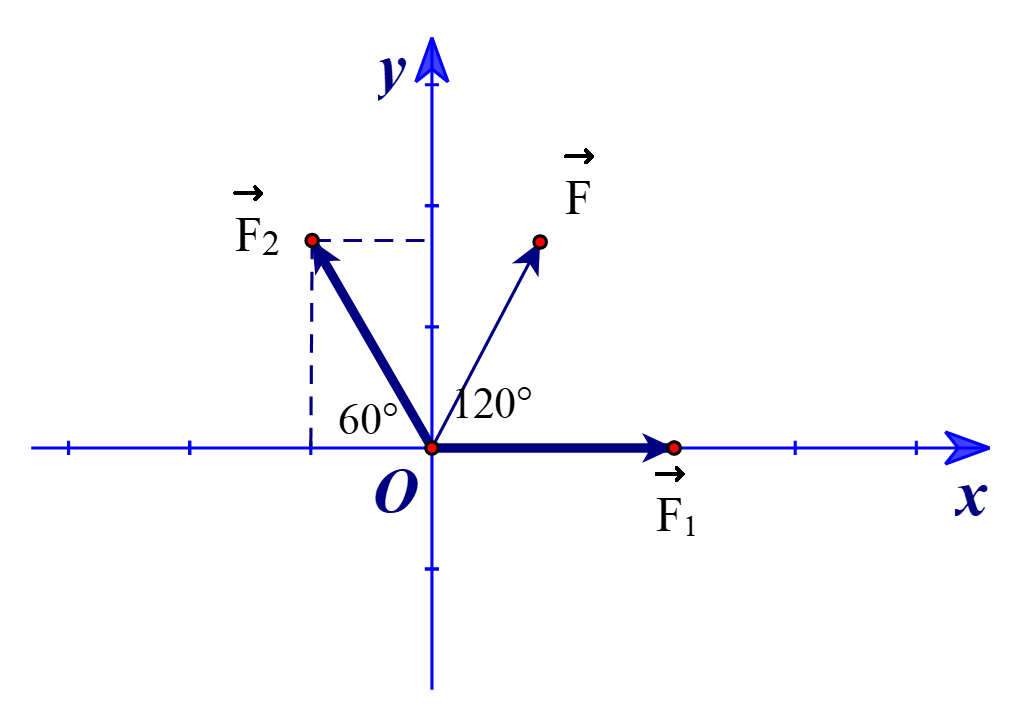
Ta có:
⦁ →F1=(100;0).
⦁ (→F1,→F2)=120∘. Suy ra tọa độ →F2=(100.cos60∘;100.sin60∘)=(50;50√3).
Do đó, lực tổng hợp →F của →F1 và →F2 có tọa độ là:
→F=→F1+→F2=(100+50;0+50√3)=(150;50√3).
Vì vậy cường độ của lực tổng hợp của →F1 và →F2 là: |→F|=√1502+(50√3)2=100√3(N).
Vậy ta chọn phương án D.