Câu hỏi:
18/07/2024 181Cho hai lực F1, F2. Biết \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có cùng cường độ lực là 100 N, góc hợp bởi \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là 120°. Khi đó cường độ lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng:
A. 100 N;
B. 50 N;
C. \(50\sqrt 3 \,\,\,N\);
D. \(100\sqrt 3 \,\,\,N\).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Gọi là lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Chọn hệ tọa độ Oxy như hình vẽ, với x và y được tính bằng đơn vị Newton.
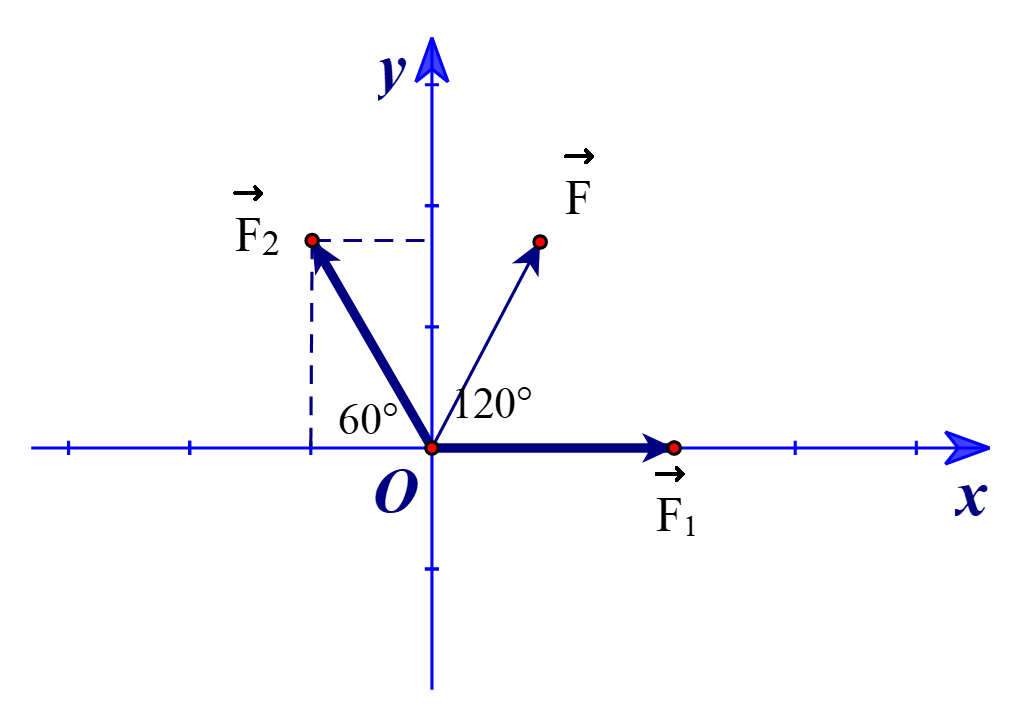
Ta có:
⦁ \(\overrightarrow {{F_1}} = \left( {100;0} \right)\).
⦁ \(\left( {\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} } \right) = 120^\circ \). Suy ra tọa độ \(\overrightarrow {{F_2}} = \left( {100.\cos 60^\circ ;100.\sin 60^\circ } \right) = \left( {50;50\sqrt 3 } \right)\).
Do đó, lực tổng hợp \(\overrightarrow F \) của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có tọa độ là:
\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \left( {100 + 50;0 + 50\sqrt 3 } \right) = \left( {150;50\sqrt 3 } \right)\).
Vì vậy cường độ của lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là: \(\left| {\overrightarrow F } \right| = \sqrt {{{150}^2} + {{\left( {50\sqrt 3 } \right)}^2}} = 100\sqrt 3 \,\,\,\left( N \right)\).
Vậy ta chọn phương án D.
Hướng dẫn giải
Đáp án đúng là: D
Gọi là lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \).
Chọn hệ tọa độ Oxy như hình vẽ, với x và y được tính bằng đơn vị Newton.

Ta có:
⦁ \(\overrightarrow {{F_1}} = \left( {100;0} \right)\).
⦁ \(\left( {\overrightarrow {{F_1}} ,\,\,\overrightarrow {{F_2}} } \right) = 120^\circ \). Suy ra tọa độ \(\overrightarrow {{F_2}} = \left( {100.\cos 60^\circ ;100.\sin 60^\circ } \right) = \left( {50;50\sqrt 3 } \right)\).
Do đó, lực tổng hợp \(\overrightarrow F \) của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) có tọa độ là:
\(\overrightarrow F = \overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \left( {100 + 50;0 + 50\sqrt 3 } \right) = \left( {150;50\sqrt 3 } \right)\).
Vì vậy cường độ của lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là: \(\left| {\overrightarrow F } \right| = \sqrt {{{150}^2} + {{\left( {50\sqrt 3 } \right)}^2}} = 100\sqrt 3 \,\,\,\left( N \right)\).
Vậy ta chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(–1; –2), B(3; 2), C(4; –1). Biết rằng điểm E(a; b) di động trên đường thẳng AB sao cho \(\left| {2\overrightarrow {EA} + 3\overrightarrow {EB} - \overrightarrow {EC} } \right|\) đạt giá trị nhỏ nhất. Khi đó a.b bằng:
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho A(3; 3), B(–1; –9), C(5; –1). Gọi I là trung điểm của AB. Tọa độ M thỏa mãn \(\overrightarrow {AM} = - \frac{1}{2}\overrightarrow {CI} \) là:
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có trọng tâm \(G\left( {\frac{2}{3};0} \right)\), biết M(1; –1) là trung điểm của cạnh BC. Tọa độ đỉnh A là:
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(3; 4), B(2; 1), C(–1; –2). Cho M(x; y) trên đoạn thẳng BC sao cho SABC = 4SABM. Khi đó x2 – y2 bằng:


