Trắc nghiệm Toán 10 Bài 6. Tích vô hướng của hai vectơ có đáp án
Trắc nghiệm Toán 10 Bài 6. Tích vô hướng của hai vectơ có đáp án
-
273 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
15/07/2024Cho →a và →b là hai vectơ cùng hướng và đều khác vectơ →0. Mệnh đề nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: →a.→b=|→a|.|→b|.cos(→a,→b).
Do →a và →b là hai vectơ cùng hướng nên (→a,→b)=00⇒cos(→a,→b)=1.
Vậy →a.→b=|→a|.|→b|.
Câu 2:
19/07/2024Cho →a và →b khác vectơ →0. Xác định góc α giữa hai vectơ →a và →b khi →a.→b=−|→a|.|→b|.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: →a.→b=|→a|.|→b|.cos(→a,→b).
Mà theo giả thiết →a.→b=−|→a|.|→b|, suy ra cos(→a,→b)=−1⇒(→a,→b)=1800.
Câu 3:
21/07/2024Cho hai vectơ →a và →b thỏa mãn |→a|=3, |→b|=2 và →a.→b=−3. Xác định góc α giữa hai vectơ →a và →b
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: →a.→b=|→a|.|→b|.cos(→a,→b)⇒cos(→a,→b)=→a.→b|→a|.|→b|=−33.2=−12⇒(→a,→b)=1200.Câu 4:
23/07/2024Cho hai vectơ →a và →b thỏa mãn |→a|=|→b|=1 và hai vectơ →u=25→a−3→b và →v=→a+→b vuông góc với nhau. Xác định góc α giữa hai vectơ →a và →b.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: →u⊥→v⇒→u.→v=0⇔(25→a−3→b)(→a+→b)=0⇔25→a2−135→a→b−3→b2=0
|→a|=|→b|=1→→a→b=−1.Suy ra cos(→a,→b)=→a.→b|→a|.|→b|=−1⇒(→a,→b)=1800.
Câu 5:
26/10/2024Cho hai vectơ →a và →b. Đẳng thức nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
* Lời giải:
Nhận thấy C và D chỉ
khác nhau về hệ số 12 và 14 nên đáp án sai rơi vào C hoặc D.
Ta có: |→a+→b|2−|→a−→b|2=(→a+→b)2−(→a−→b)2
=→a2+→b2+2→a.→b−→a2−→b2+2→a.→b=4→a.→b
⇒→a.→b=14(|→a+→b|2−|→a−→b|2).
- A đúng, vì:
|→a+→b|2=(→a+→b)2=(→a+→b).(→a+→b)
=→a.→a+→a.→b+→b.→a+→b.→b=|→a|2+|→b|2+2→a.→b⇒→a.→b=12(|→a+→b|2−|→a|2−|→b|2).
· B đúng, vì
|→a−→b|2=(→a−→b)2=(→a−→b).(→a−→b)
=→a.→a−→a.→b−→b.→a+→b.→b=|→a|2+|→b|2−2→a.→b⇒→a.→b=12(|→a|2+|→b|2−|→a−→b|2).
* Phương pháp giải:
- xét các câu trả lời:
+ sử dụng các tính chất về tích của hai vectơ:
+) Tích vô hướng
→a.→a→a.→a được kí hiệu là →a2→a2 và ta có: →a2=∣∣→a∣∣2→a2=|→a|2.+ sử dụng cả hằng đẳng thức vào bài toán để biến đổi
* Lý thuyết cần nắm thêm về tích vô hướng của hai vectơ:
- Định nghĩa góc giữa hai vectơ: Cho hai vectơ
→a→a và →b→b đều khác vectơ →0→0. Từ điểm O bất kì vẽ −−→OA=→a→OA=→a, −−→OB=→b→OB=→b, khi đó góc ˆAOB^AOB (0o≤ˆAOB≤180o0o≤^AOB≤180o) là góc giữa hai vectơ →a→a và →b→b. Kí hiệu: (→a,→b)(→a,→b).
- Định nghĩa tích vô hướng: Cho hai vectơ →a→a và →b→b (→a,→b≠→0→a,→b≠→0), khi đó tích vô hướng của →a→a và →b→b kí hiệu là →a.→b→a.→b và xác định bởi công thức: →a.→b=∣∣→a∣∣.∣∣∣→b∣∣∣.cos(→a,→b)→a.→b=|→a|.|→b|.cos(→a,→b).
- Chú ý:
+) Khi ít nhất một trong hai vectơ →a→a và →b→b bằng vectơ →0→0 ta quy ước: →a.→b=0→a.→b=0.
+) Với hai vectơ →a→a và →b→b (), ta có: →a.→b=0⇔→a⊥→b→a.→b=0⇔→a⊥→b.
- Các tính chất của tích vô hướng:
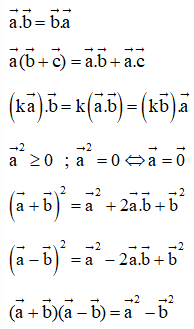
- Ứng dụng của tích vô hướng:
+) Độ dài của vectơ →a=(a1;a2)→a=(a1;a2) được tính theo công thức: ∣∣→a∣∣=√a12+a22|→a|=√a12+a22
+) Góc giữa hai vectơ →a=(a1;a2)→a=(a1;a2) và →b=(b1;b2)→b=(b1;b2) ( →a;→b≠→0→a;→b≠→0):
cos(→a;→b)=→a.→b∣∣→a∣∣.∣∣∣→b∣∣∣=a1b1+a2b2√a21+a22.√b21+b22cos(→a;→b)=→a.→b|→a|.|→b|=a1b1+a2b2√a21+a22.√b21+b22
+) Khoảng cách giữa hai điểm A(xA;yA)A(xA;yA) và B(xB;yB)B(xB;yB) được tính theo công thức:
AB=√(xB−xA)2+(yB−yA)2AB=√(xB−xA)2+(yB−yA)2
CÁC DẠNG TOÁN:
Dạng 1: Tính tích vô hướng của hai vectơ, góc giữa hai vectơ.
Phương pháp giải:
- Tính tích vô hướng: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc đưa hai vectơ về các vectơ vuông góc. Sau đó, áp dụng công thức định nghĩa, tính chất và hằng đẳng thức để tính tích vô hướng của hai vectơ. Đối với hai vectơ biết tọa độ thì tính theo công thức →a.→b=a1b1+a2b2→a.→b=a1b1+a2b2
- Tính góc giữa hai vectơ: Phân tích vectơ và đưa hai vectơ về chung gốc để tìm góc giữa hai vectơ hoặc dùng công thức: cos(→a;→b)=→a.→b∣∣→a∣∣.∣∣∣→b∣∣∣=a1b1+a2b2√a21+a22.√b21+b22
Dạng 2: Tính độ dài đoạn thẳng, độ dài vectơ.
Phân tích vectơ để biến phép tính độ dài đoạn thẳng thành phép tính tích vô hướng, áp dụng công thức AB2=|→AB|2=→AB2. Nếu đề bài có liên quan đến tọa độ thì áp dụng công thức: |→AB|=AB=√(xB−xA)2+(yB−yA)2.
Xem thêm các bài viết liên quan hay, chi tiết:
Tích vô hướng của hai vectơ và cách giải bài tập (2024) chi tiết nhất
Sách bài tập Toán 10 Bài 6 (Cánh diều): Tích vô hướng của hai vectơ
Trắc nghiệm Toán 10 Cánh diều Bài 6. Tích vô hướng của hai vectơ có đáp án (Phần 2)
Câu 6:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xác định được góc (→AB,→AC) là góc ˆA nên (→AB,→AC) (do tam giác ABC đều)
Do đó →AB.→AC=AB.AC.cos(→AB,→AC)=a.a.cos600=a22.
Câu 7:
21/07/2024Cho tam giác đều ABC có cạnh bằng a Tính tích vô hướng →AB.→BC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xác định được góc (→AB,→BC) là góc ngoài của góc ˆB nên (→AB,→BC)=1200 (do tam giác ABC là tam giác đều nên góc ˆB=60°, do đó, góc ngoài của góc B có số đo là 120o).
Do đó
Câu 8:
11/11/2024Gọi G là trọng tâm tam giác đều ABC có cạnh bằng a. Mệnh đề nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Lời giải
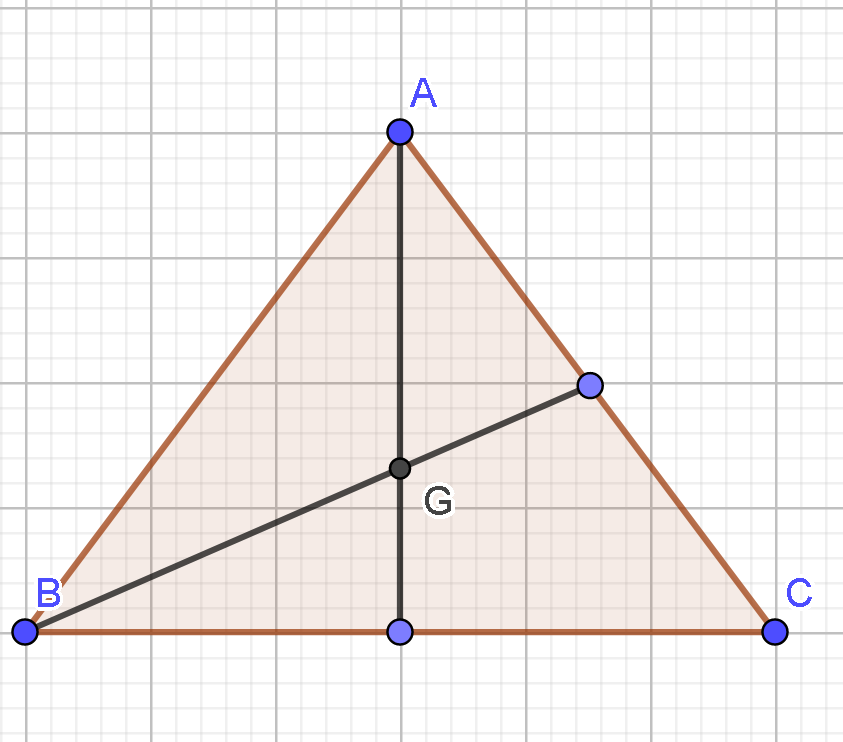
- Xác định được góc là góc nên (do tam giác ABC đều)
Do đó A đúng
- Xác định được góc là góc ngoài của góc nên
Do đó B đúng.
Xác định được góc là góc nên
Ta có: AG nằm trên đường trung tuyến cũng chính là đường cao của tam giác đều ABC, ta tính được đường cao, suy ra: AG = .a.= .
Tương tự, GB = .
Do đó C sai.
Xác định được góc là góc nên
Do đó D đúng.
*Phương pháp giải:
Xét tính đúng sai của từng đáp án và kết luận
*Lý thuyết:
- Định nghĩa: Cho hai vectơ và đều khác vectơ . Từ một điểm O bất kì, ta vẽ hai vectơ và . Khi đó, góc với số đo từ đến được gọi là góc giữa hai vectơ và .
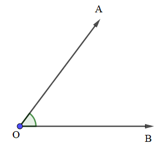
- Kí hiệu góc giữa hai vectơ và :
- Chú ý: Với hai vectơ và đều khác vectơ .
+ Nếu = hoặc ,
+ Nếu = Hai vectơ và cùng hướng.
+ Nếu = Hai vectơ và ngược hướng.
Công thức tính góc giữa hai vecto
- Cho hai vectơ và đều khác vectơ ta có:
( )
- Cho hai vectơ và đều khác vectơ ta có:
- Lưu ý: Góc giữa hai vectơ luôn có số đo từ đến .
Xem thêm
Lý thuyết Vectơ trong không gian– Toán lớp 12 Kết nối tri thức
Câu 9:
22/07/2024Cho tam giác đều ABC có cạnh bằng a và chiều cao AH. Mệnh đề nào sau đây là sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
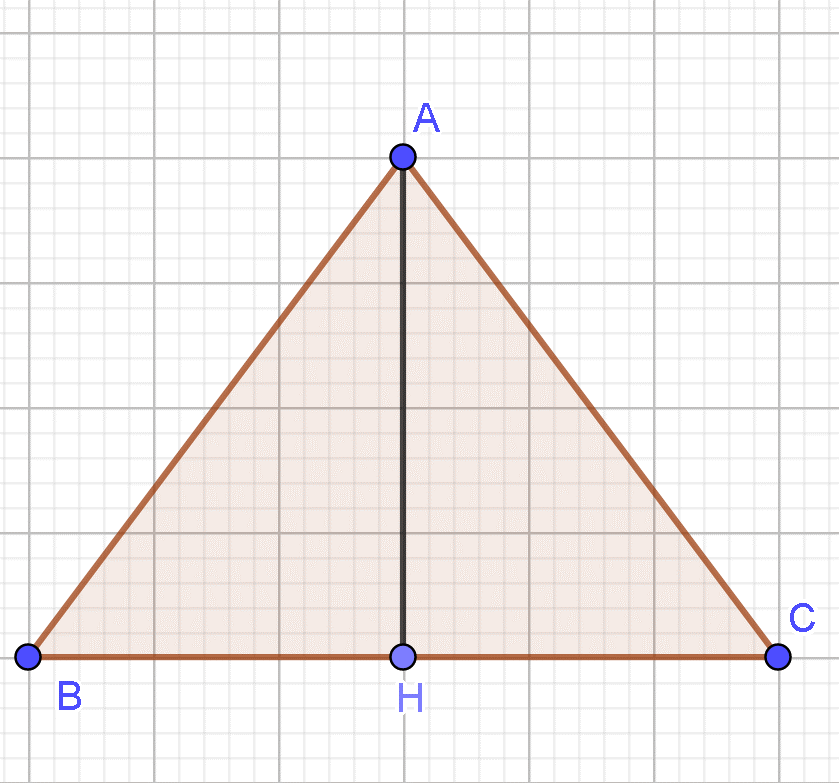
Xác định được góc là góc ngoài của góc nên (vì tam giác ABC đều nên góc A = 60o, do đó góc ngoài của góc A bằng 120o).
Do đó
+) A đúng vì nên suy ra
+) B đúng vì AH chính là tia phân giác nên
+) C đúng vì
Câu 10:
21/07/2024Cho tam giác ABC vuông cân tại A và có Tính
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
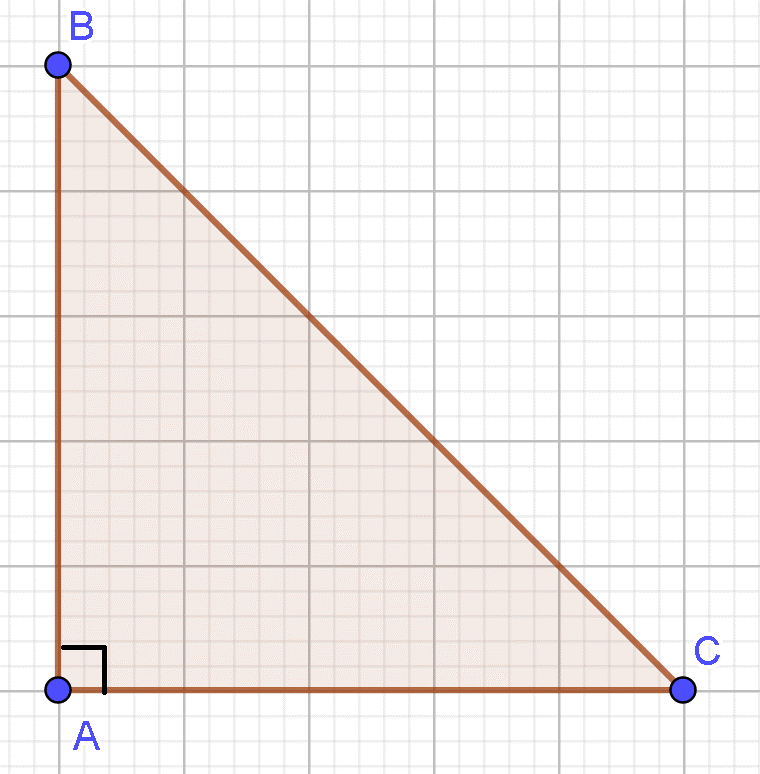
Xác định được góc là góc ngoài của góc ![]() nên (Tam giác ABC vuông cân tại A, suy ra góc )
nên (Tam giác ABC vuông cân tại A, suy ra góc )
Độ dài BC là:
Do đó
Câu 11:
12/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
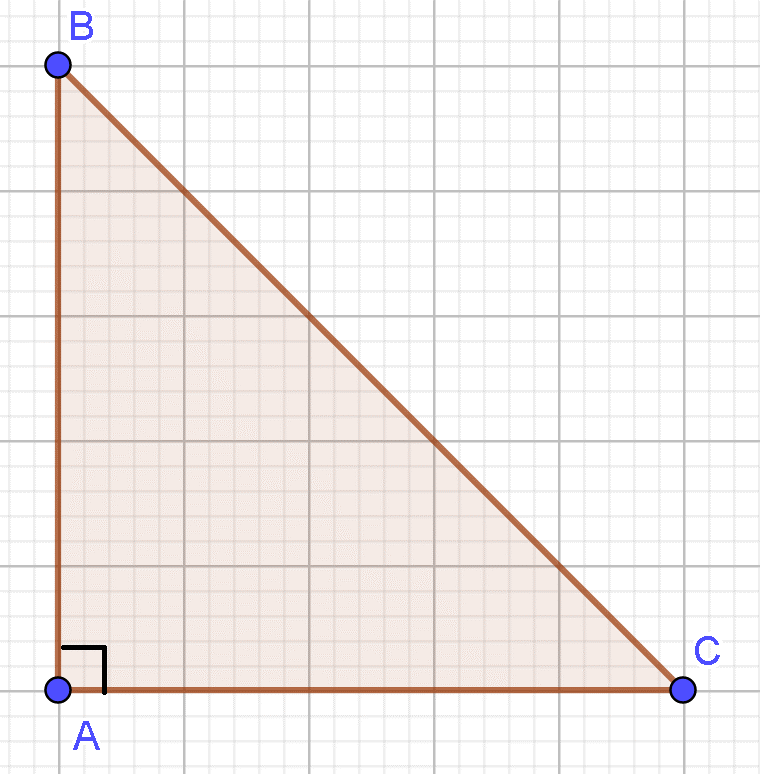
Do tam giác ABC vuông cân tại A nên suy ra = 0
Câu 12:
14/07/2024Cho tam giác ABC vuông tại A và có AB = c; AC = b. Tính
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
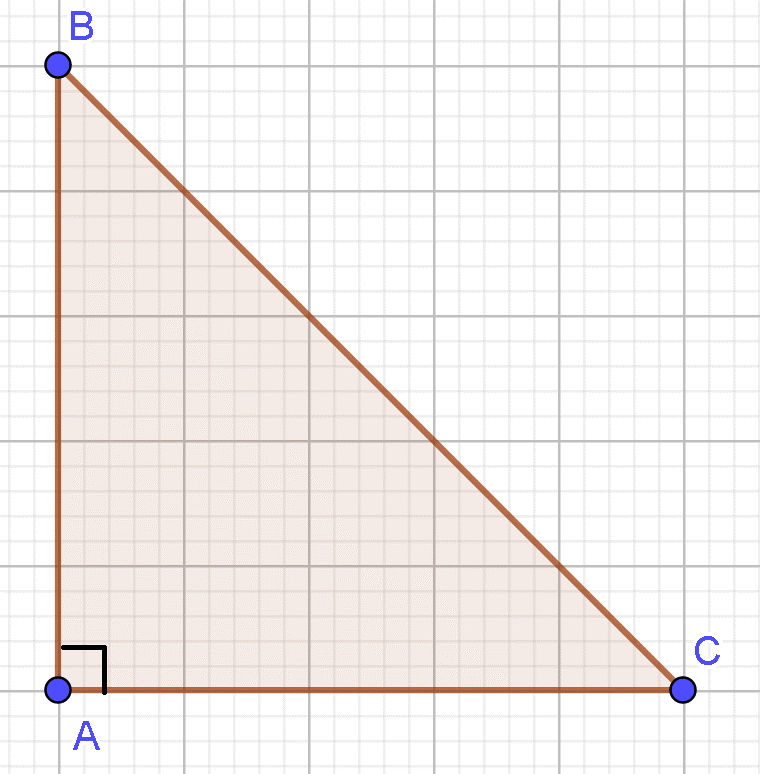
Áp dung định lý Py – ta – go ta có:
Cos B =
Lại có: cos B chính là cos
Ta có:
Câu 14:
23/07/2024Cho tam giác ABC có Gọi M là trung điểm cạnh BC Tính
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì M là trung điểm của BC suy ra
Khi đó
Câu 15:
21/07/2024Cho ba điểm O, A, B không thẳng hàng. Điều kiện cần và đủ để tích vô hướng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có:
Do đó, tam giác OAB cân tại O.
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 6. Tích vô hướng của hai vectơ có đáp án (272 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 6. Tích vô hướng của hai vectơ có đáp án (Phần 2) (617 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án (1165 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2) (732 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 5. Tích Của Một Số Với Một Vectơ có đáp án (Phần 2) (667 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 1. Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác có đáp án (phần 2) (661 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 4. Tổng và hiệu của hai vectơ có đáp án (Phần 2) (595 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 3. Vectơ có đáp án (Phần 2) (590 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2) (585 lượt thi)
- Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0 độ đến 180 độ . Định lý cosin và sin trong tam giác có đáp án (468 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Khái niệm vectơ có đáp án (406 lượt thi)
- Trắc nghiệm Toán 10 Bài 4. Tổng và hiệu hai vectơ có đáp án (389 lượt thi)
