Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0 độ đến 180 độ . Định lý cosin và sin trong tam giác có đáp án
Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0 độ đến 180 độ . Định lý cosin và sin trong tam giác có đáp án
-
425 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Tam giác ABC có . Số đo góc bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Theo định lí hàm cosin, ta có: .
Do đó, .
Câu 2:
13/07/2024Tam giác ABC có và . Tính độ dài cạnh BC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Theo định lí hàm cosin, ta có:
.Câu 3:
19/07/2024Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và . Tính độ dài cạnh cạnh BC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
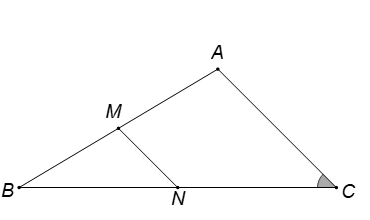
Gọi M, N lần lượt là trung điểm của AB, BC.
MN là đường trung bình của .
. Mà MN = 3, suy ra AC = 6.
Theo định lí hàm cosin, ta có:
- 6.BC - 45 = 0
BC = 3 + 3
Câu 4:
16/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo định lí hàm cosin, ta có:
- .BC + 1 = 0
.
Câu 5:
23/07/2024Tam giác ABC có và AB = 5. Tính độ dài cạnh AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo định lí hàm sin, ta có:
.Câu 6:
06/10/2024Cho hình thoi ABCD cạnh bằng 1cm và có . Tính độ dài AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
*Phương pháp giải:
- Dựa vào tính chất của hình thoi chúng ta có thể xác định được số đo của góc ABC khi đã biết được số đo của góc BAD.
- Áp dụng định lí hàm cosin vào tam giác ABC để tính cạnh AC khi đã biết được số đo các cạnh của hình thoi và số đo góc ABC.
* Lời giải:
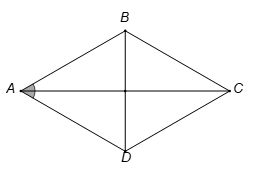
Do ABCD là hình thoi, có .
Theo định lí hàm cosin, ta có:
* Một số kiến thức liên quan về định lí cosin và định lí sin trong tam giác
- Định lí côsin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:

a2 = b2 + c2 – 2bc.cosA;
b2 = c2 + a2 – 2ca.cosB;
c2 = a2 + b2 – 2ab.cosC.
Từ định lí côsin, ta có hệ quả sau đây:
Hệ quả:
cosA =
cosB =
cosC = .
- Định lí sin: Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
= 2R
trong đó R là bán kính đường tròn ngoại tiếp tam giác ABC.
Từ định lí sin, ta có hệ quả sau đây:
Hệ quả:
a = 2R.sinA; b = 2R.sinB; c = 2R.sinC;
Xem thêm các bài viết liên quan hay, chi tiết:
Giải SGK Toán 10 Bài 2 (Chân trời sáng tạo): Định lí côsin và định lí sin .
Trắc nghiệm Toán 10 Bài 2: Định lí côsin và định lí sin - Chân trời sáng tạo.
Câu 7:
18/07/2024Tam giác ABC có . Điểm M thuộc đoạn BC sao cho MC = 2MB. Tính độ dài cạnh AM..
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
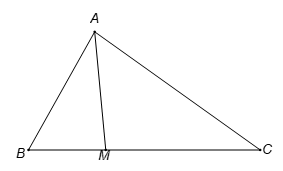
Theo định lí hàm cosin, ta có : .
Do . Theo định lí hàm cosin, ta có:
Câu 8:
12/07/2024 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Theo định lí hàm cosin, ta có:
Trong có .
Câu 9:
15/07/2024Tam giác ABC có và . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Áp dụng định lí Cosin, ta có
Suy ra tam giác ABC vuông tại B do đó bán kính
Câu 10:
22/07/2024Tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc bằng nhau. Đặt . Trong các hệ thức sau, hệ thức nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
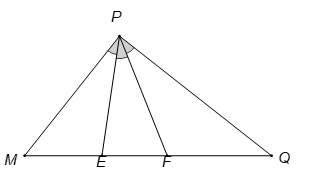
Ta có: .
Theo định lí hàm cosin, ta có:
Câu 11:
19/07/2024Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Độ dài lớn nhất của đoạn OB bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
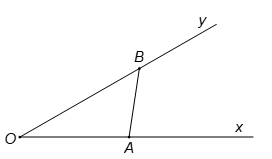
Theo định lí hàm sin, ta có:
Do đó, độ dài OB lớn nhất khi và chỉ khi
.
Khi đó OB = 2.
Câu 12:
19/07/2024Cho góc . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
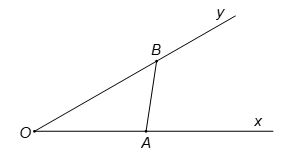
Theo định lí hàm sin, ta có:
Do đó, độ dài OB lớn nhất khi và chỉ khi: .
Khi đó OB = 2. Tam giác OAB vuông tại .
Câu 13:
12/11/2024Tam giác ABC có . Các cạnh a, b, c liên hệ với nhau bởi đẳng thức . Khi đó góc bằng bao nhiêu độ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
*Lời giải:
Theo định lí hàm cosin, ta có: .
Mà
(do )
Khi đó, .
*Phương pháp giải:
- Áp dụng định lý cosin trong tam giác:
Định lí côsin
Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:
a2 = b2 + c2 – 2bccosA,
b2 = c2 + a2 – 2cacosB,
c2 = a2 + b2 – 2abcosC.
Lưu ý:
cosA = ,
cosB = ,
cosC = .
*Các dạng bài tập về giá trị lượng giác của một góc từ 0 độ đến 180 độ:
- Từ định nghĩa ta có:
tanα =sinαcosα(α≠90°);cotα=cosαsinα(α≠0°và α≠180°);tanα=1cotα (α∉{0°;90°;180°})
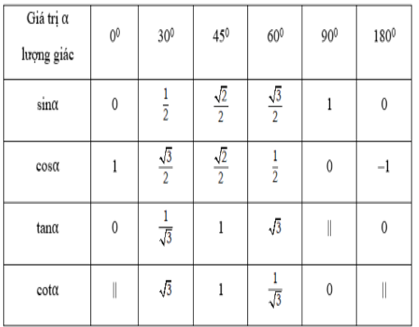
- Bảng giá trị lượng giác (GTLG) của một số góc đặc biệt:
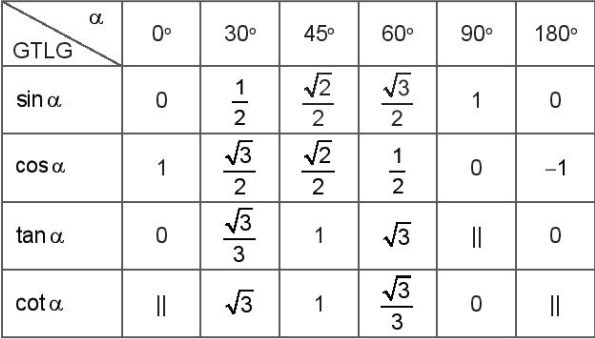
Chú ý: Kí hiệu || chỉ giá trị lượng giác tương ứng không xác định.
- Tính chất:
Hai góc bù nhau là hai góc có tổng bằng . Cho góc ta có:
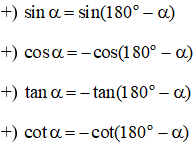
Hai góc phụ nhau là hai học có tổng bằng . Cho góc ta có:
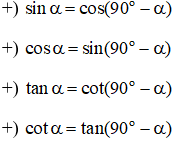
- Bảng giá trị lượng giác của các góc đặc biệt:
- Định nghĩa góc giữa hai vectơ: Cho hai vectơ và đều khác vectơ . Từ điểm O bất kì vẽ , , khi đó góc () là góc giữa hai vectơ và . Kí hiệu: .
- Các hệ thức cơ bản liên hệ giữa các giá trị lượng giác :
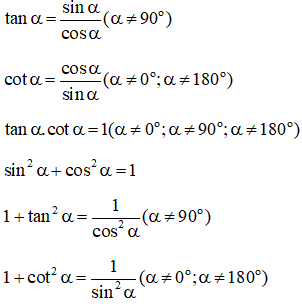
- Chú ý:
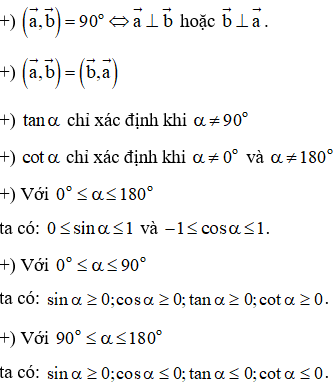
Định lí côsin
Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó:
a2 = b2 + c2 – 2bccosA,
b2 = c2 + a2 – 2cacosB,
c2 = a2 + b2 – 2abcosC.
Lưu ý:
cosA = ,
cosB = ,
cosC = .
Định lí sin
Cho tam giác ABC có BC = a, CA = b, AB = c và bán kính đường tròn ngoại tiếp là R. Khi đó:
Lưu ý:
a = 2RsinA,
b = 2RsinB,
c = 2RsinC.
Các dạng bài.
Dạng 1: Góc và dấu của các giá trị lượng giác.
Phương pháp giải:
Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất và bảng giá trị lượng giác đặc biệt và các chú ý về dấu của giá trị lượng giác liên quan tới góc.
Dạng 2: Cho một giá trị lượng giác, tính các giá trị lượng giác còn lại.
Phương pháp giải:
Áp dụng định nghĩa giá trị lượng giác của một góc, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác để từ một giá trị lượng giác suy ra các giá trị lượng giác còn lại.
Dạng 3: Chứng minh, rút gọn một biểu thức lượng giác.
Phương pháp giải:
Áp dụng định nghĩa giá trị lượng giác của một góc, bảng các giá trị lượng giác đặc biệt, tính chất của giá trị lượng giác đặc biệt, các hệ thức cơ bản liên hệ giữa các giá trị lượng giác, hằng đẳng thức để rút gọn biểu thức lượng giác hay chứng minh một đẳng thức lượng giác ( bằng cách chứng minh hai vế bằng nhau hoặc từ đẳng thức đã cho biến đổi về một đẳng thức được công nhận là đúng).
Xem thêm các bài viết liên quan hay, chi tiết:
Giá trị lượng giác của một góc bất kì từ 0 đến 180 và cách giải bài tập (2024) chi tiết nhất
Câu 14:
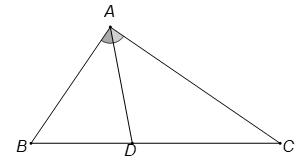
15/07/2024Tam giác ABC vuông tại A, có . Gọi m là độ dài đoạn phân giác trong góc . Tính m theo b và c.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: .
Do AD là phân giác trong của
.
Theo định lí hàm cosin, ta có:
hay .
Câu 15:
12/07/2024Tam giác ABC có BC = 10 và . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Áp dụng định lí sin, ta có:
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 1. Giá trị lượng giác của một góc từ 0 độ đến 180 độ . Định lý cosin và sin trong tam giác có đáp án (424 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 1. Giá trị lượng giác của một góc từ 0° đến 180°. Định lí côsin và định lí sin trong tam giác có đáp án (phần 2) (587 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Toán 10 Bài 2. Giải tam giác. Tính diện tích tam giác có đáp án (1122 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 2. Giải Tam Giác có đáp án (Phần 2) (669 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 5. Tích Của Một Số Với Một Vectơ có đáp án (Phần 2) (590 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 6. Tích vô hướng của hai vectơ có đáp án (Phần 2) (539 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 4. Tổng và hiệu của hai vectơ có đáp án (Phần 2) (506 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài tập cuối chương 4 có đáp án (Phần 2) (495 lượt thi)
- Trắc nghiệm Toán 10 Cánh diều Bài 3. Vectơ có đáp án (Phần 2) (484 lượt thi)
- Trắc nghiệm Toán 10 Bài 3. Khái niệm vectơ có đáp án (358 lượt thi)
- Trắc nghiệm Toán 10 Bài 4. Tổng và hiệu hai vectơ có đáp án (349 lượt thi)
- Trắc nghiệm Toán 10 Bài 5. Tích của một số với một vectơ có đáp án (337 lượt thi)
