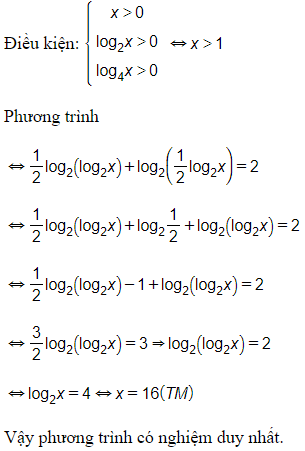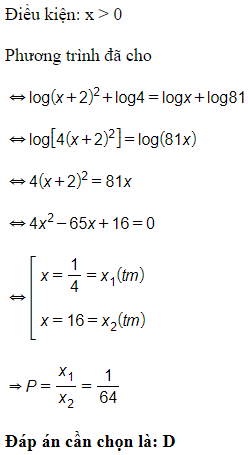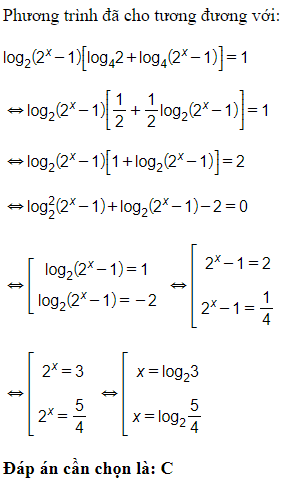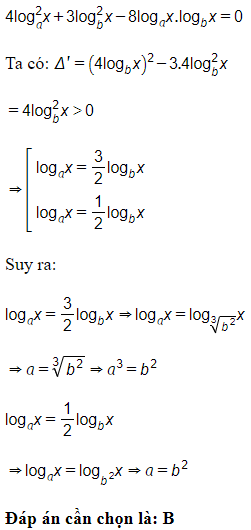Trắc nghiệm Phương trình mũ và phương trình Logarit (có đáp án)
Trắc nghiệm Toán 12 Bài 5: Phương trình mũ và phương trình Logarit
-
335 lượt thi
-
30 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Phương trình 42x+5=22−x có nghiệm là:
 Xem đáp án
Xem đáp án
⇔24x+10=22−x
⇔4x+10=2−x
⇔x=−85
Đáp án cần chọn là: A
Câu 2:
12/07/2024Tổng các nghiệm của phương trình 3x4−3x2=81
 Xem đáp án
Xem đáp án
⇔x4−3x2−4=0
⇔x2=4⇔x=±2
Tổng các nghiệm sẽ bằng 0
Đáp án cần chọn là: A
Câu 4:
23/07/2024Phương trình 2x−1−2x2−x=(x−1)2 có tất cả bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Phương trình
2x−1−2x2−x=(x−1)2
(*)
Xét hàm số f'
Suy ra hàm số
Nhận thấy
Vậy phương trình có một nghiệm duy nhất
Chọn A.
Câu 6:
21/07/2024Giải phương trình log4(x+1)+log4(x−3)=3
 Xem đáp án
Xem đáp án
Điều kiện:
Ta có:
So sánh với điều kiện nghiệm của pt là
Đáp án cần chọn là: B
Câu 7:
20/07/2024Tổng lập phương các nghiệm của phương trình bằng:
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình đã cho
Đáp án cần chọn là: C
Câu 8:
12/07/2024Tính tổng tất cả các nghiệm của phương trình [0;π].
 Xem đáp án
Xem đáp án
Phương trình
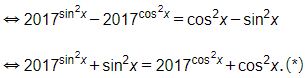
Xét hàm số
Suy ra hàm số
Nhận thấy
Vì
Chọn A.
Câu 9:
23/07/2024Phương trình có bao nhiêu nghiệm không âm?
 Xem đáp án
Xem đáp án
Phương trình tương đương với .
Đặt
Với
Vậy chỉ có duy nhất nghiệm là nghiệm không âm.
Chọn B.
Câu 10:
20/07/2024Tập nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện:
Với điều kiện này thì phương trình đã cho tương đương với
Vậy tập nghiệm của phương trình đã cho là
Đáp án cần chọn là: D
Câu 11:
20/07/2024Tính tổng tất cả các nghiệm của phương trình [0;3π].
 Xem đáp án
Xem đáp án
Điều kiện:
Ta có
Vì
Chọn C.
Câu 12:
23/07/2024Tính P là tích tất cả các nghiệm của phương trình =0
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình đã cho
(tm)
Đáp án cần chọn là: C
Câu 14:
13/07/2024Giải phương trình , ta có nghiệm là:
 Xem đáp án
Xem đáp án
Điều kiện: x >
(tm)
Đáp án cần chọn là: D
Câu 15:
22/07/2024Tập nghiệm của phương trình log2(x2−x+2)=1
 Xem đáp án
Xem đáp án
Điều kiện: (luôn đúng với mọi x)
Khi đó phương trình tương đương:
Vậy tập nghiệm của phương trình là:
Đáp án cần chọn là: B
Câu 19:
22/07/2024Tìm tích các nghiệm của phương trình (√2−1)x+(√2+1)x−2√2=0
 Xem đáp án
Xem đáp án
Đặt phương trình có dạng
Khi đó:
Suy ra tích các nghiệm bằng – 1.
Đáp án cần chọn là: B
Câu 21:
15/07/2024Phương trình có tất cả bao nhiêu nghiệm?
 Xem đáp án
Xem đáp án
Điều kiện:
Phương trình đã cho
Đáp án cần chọn là: A
Câu 25:
21/07/2024Tìm m để phương trình x∈(1;3)
 Xem đáp án
Xem đáp án
Đặt
Xét hàm số trên (2; 8) có:
Bảng biến thiên:
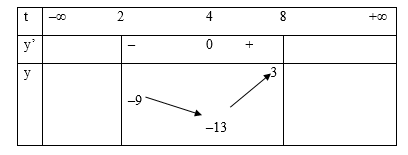
Căn cứ bảng biến thiên:
Phương trình
Đáp án cần chọn là: A
Câu 26:
11/07/2024Tìm giá trị của tham số m để phương trình x1+x2=3
 Xem đáp án
Xem đáp án
Phương trình tương đương với: (*)
Đặt
Giả sử phương trình có 2 nghiệm lần lượt là nghiệm của (*)
Suy ra:
Đáp án cần chọn là: D
Câu 27:
17/07/2024Tính tổng T tất cả các nghiệm của phương trình [0;2π]
 Xem đáp án
Xem đáp án
Ta có:
Do
Đáp án cần chọn là: D
Câu 28:
23/07/2024Số nghiệm thực phân biệt của phương trình là:
 Xem đáp án
Xem đáp án
Điều kiện:
Với x < 0 ta có:
Phương trình không có nghiệm x < 0.
Với x > 0, áp dụng bất đẳng thức Cô si cho hai số dương ta được:
Dấu “=” xảy ra khi và chỉ khi:
(không xảy ra)
Vậy nên phương trình vô nghiệm.
Đáp án cần chọn là: D
Câu 29:
21/07/2024Tìm giá trị m để phương trình có nghiệm duy nhất
 Xem đáp án
Xem đáp án
Đặt |x−1|=ax−1=a khi đó phương trình trở thành 2a+1+2a+m=02a+1+2a+m=0 (1)
Để phương trình đã cho có nghiệm duy nhất thì pt (1) bắt buộc phải có nghiệm duy nhất a = 0 (vì nếu a > 0 thì sẽ tồn tại 2 giá trị của x)
Nên 21+20+m=021+20+m=0
⇒m=−3⇒m=−3
Đáp án cần chọn là: C
Câu 30:
21/07/2024Tìm tất cả các giá trị thực của m để phương trình có 3 nghiệm thực phân biệt:
 Xem đáp án
Xem đáp án
TXĐ: D = R
Xét hàm
ta có:
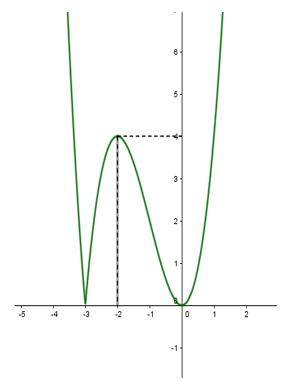
Để phương trình có 3 nghiệm phân biệt thì
Đáp án cần chọn là: D
Có thể bạn quan tâm
- Trắc nghiệm Phương trình mũ và phương trình Logarit (có đáp án) (334 lượt thi)
- 33 câu trắc nghiệm: Phương trình mũ và phương trình lôgarit có đáp án (324 lượt thi)
- Trắc nghiệm Phương trình mũ và phương trình logarit có đáp án (Nhận biết) (313 lượt thi)
- Trắc nghiệm Phương trình mũ và phương trình logarit có đáp án (Thông hiểu) (281 lượt thi)
- Trắc nghiệm Phương trình mũ và phương trình logarit có đáp án (Vận dụng) (356 lượt thi)
- Trắc nghiệm Phương trình mũ và phương trình logarit có đáp án (303 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Logarit có đáp án (Thông hiểu) (1214 lượt thi)
- 200 câu trắc nghiệm Hàm số mũ và Logarit cơ bản (P1) (836 lượt thi)
- Trắc nghiệm Logarit có đáp án (Nhận biết) (741 lượt thi)
- Trắc nghiệm Logarit (có đáp án) (683 lượt thi)
- Trắc nghiệm Lũy thừa có đáp án (Nhận biết) (591 lượt thi)
- Trắc nghiệm Bất phương trình mũ và bất phương trình Logarit (có đáp án) (581 lượt thi)
- Trắc nghiệm Lũy thừa có đáp án (Vận dụng) (575 lượt thi)
- Trắc nghiệm Lũy thừa (có đáp án) (516 lượt thi)
- Trắc nghiệm Logarit có đáp án (513 lượt thi)
- Trắc nghiệm Hàm số mũ. Hàm số Logarit (có đáp án) (498 lượt thi)