Câu hỏi:
21/07/2024 244Tìm tất cả các giá trị thực của m để phương trình 2log2|x|+log2|x+3|=m có 3 nghiệm thực phân biệt:
A. m∈(0;2)
B. m∈{0;2}
C. m∈(−∞;2)
D. m∈{2}
Đáp án chính xác
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
TXĐ: D = R
2log2|x|+log2|x+3|=m
⇔log2|x|2+log2|x+3|=m
⇔log2(|x|2.|x+3|)=m
⇔|x|2.|x+3|=2m
⇔x2.|x+3|=2m
Xét hàm f(x)=x2.|x+3|
ta có: f(x)=x2.|x+3|
=|x3+3x2|
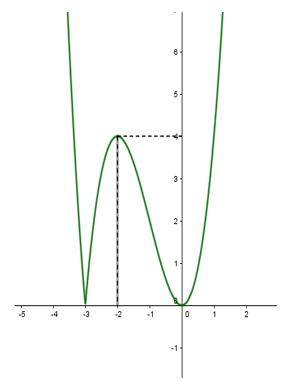
Để phương trình có 3 nghiệm phân biệt thì 2m=4⇔m=2
Đáp án cần chọn là: D
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Cho a, b, x là các số thực dương khác 1 thỏa : 4log2ax+3log2bx=8logax.logbx (1). Mệnh đề (1) tương đương với mệnh đề nào sau đây:
Xem đáp án »
22/07/2024
357
Câu 9:
Tìm giá trị m để phương trình 2|x−1|+1+2|x−1|+m=0 có nghiệm duy nhất
Xem đáp án »
21/07/2024
300
Câu 12:
Phương trình log2(x−3)+2log43.log3x=2 có tất cả bao nhiêu nghiệm?
Xem đáp án »
15/07/2024
284


