28 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 12 Bài 6: Bất phương trình mũ và bất phương trình Logarit

Câu 1:

12/07/2024

Tìm tập nghiệm S của bất phương trình )3.

Xem đáp án

Đáp án: B

Giải thích:

Lời giải.

Vì $\frac{2}{\sqrt{5}} < 1$ nên bất phương trình

$\Leftrightarrow \frac{1}{x} \geq 3 \Leftrightarrow \frac{1 - 3 x}{x} \geq 0$

.

Câu 2:

23/07/2024

Tìm tất cả các giá trị của x thỏa mãn )x−1.

A. x≤−2

B. x≥4

C. −2≤x≤4

D. x≤−2x≤−2; x≥4

Xem đáp án

Đáp án: D

Giải thích:

Lời giải.

Do $\Leftrightarrow x^{2} - x - 9 \geq x - 1$

$\Leftrightarrow x^{2} - 2 x - 8 \geq 0$

.

Câu 3:

22/07/2024

Có bao nhiêu giá trị nguyên của trong đoạn $[- 2017; 2017]$ thỏa mãn bất phương trình

A. 2013

B. 2017

C. 2014

D. 2021

Xem đáp án

Đáp án: C

Giải thích:

Lời giải.

Bất phương trình $4^{x} {.3}^{3} > 3^{x} {.4}^{3}$

$\Leftrightarrow \frac{4^{x}}{3^{x}} > \frac{4^{3}}{3^{3}}$

$\Leftrightarrow {(\frac{4}{3})}^{x} > {(\frac{4}{3})}^{3}$

$\Leftrightarrow x > 3.$

Vì x nguyên và thuộc đoạn $[- 2017; 2017]$

$\overset{}{\to} x = \{4; 5; 6; ...2017\}$ .

Vậy có tất cả 2014 giá trị thỏa mãn.

Câu 4:

20/07/2024

Có tất cả bao nhiêu giá trị nguyên dương của x thỏa mãn bất phương trình $8^{x} {.2}^{1 - x^{2}} > {(\sqrt{2})}^{2 x}$ ?

A. 2

B. 3

C. 4

D. 5

Xem đáp án

Đáp án: A

Giải thích:

Lời giải.

Bất phương trình $8^{x} {.2}^{1 - x^{2}} > {(\sqrt{2})}^{2 x}$

$\Leftrightarrow 2^{3 x} {.2}^{1 - x^{2}} > 2^{x}$

$\Leftrightarrow 2^{3 x + 1 - x^{2}} > 2^{x}$

$\Leftrightarrow 3 x + 1 - x^{2} > x$

$\Leftrightarrow x^{2} - 2 x - 1 < 0$

$\Leftrightarrow 1 - \sqrt{2} < x < 1 + \sqrt{2}$

Vậy tập nghiệm của bất phương trình là $S = (1 - \sqrt{2}; 1 + \sqrt{2})$ .

Suy ra các giá trị nguyên dương thuộc S là $\{1; 2\} .$

Câu 5:

19/07/2024

Gọi là tập nghiệm của bất phương trình $P = b + a . \log_{2} 3.$

A. P=2

B. P=1

C. P=0

D. P=2 $\log_{2} 3$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải.

Bất phương trình $\Leftrightarrow \frac{3}{3^{x}} + {2.3}^{x} \leq 7$

$\Leftrightarrow {2.3}^{2 x} - {7.3}^{x} + 3 \leq 0.$

Đặt $t > 0$ .

Bất phương trình trở thành $2 t^{2} - 7 t + 3 \leq 0$

$\Leftrightarrow \frac{1}{2} \leq t \leq 3$ .

$\overset{}{\to} \frac{1}{2} \leq 3^{x} \leq 3$

$\Leftrightarrow - \log_{3} 2 \leq x \leq 1$

$\overset{}{\to} \{\begin{cases} a = - \log_{3} 2 \\ b = 1 \end{cases}$

→P=b+a.log23=0.

Câu 6:

23/07/2024

Gọi a, b lần lượt là nghiệm nhỏ nhất và nghiệm lớn nhất của bất phương trình

A. P=1

B. P= $\frac{3}{2}$

C.P=2

D.P= $\frac{5}{2}$

Xem đáp án

Đáp án: C

Giải thích:

Lời giải.

Bất phương trình tương đương với ${3.3}^{2 x} - {10.3}^{x} + 3 \leq 0$ .

Đặt $3 t^{2} - 10 t + 3 \leq 0$

$\Leftrightarrow \frac{1}{3} \leq t \leq 3$ .

$\overset{}{\to} \frac{1}{3} \leq 3^{x} \leq 3$

$\Leftrightarrow - 1 \leq x \leq 1$

$\overset{}{\to} \{\begin{cases} a = - 1 \\ b = 1 \end{cases}$

→P=b−a=2.

Câu 7:

22/07/2024

Tìm tập nghiệm S của bất phương trình ${(x^{2} + x + 1)}^{x} < 1.$

A. S=(0;+∞)

B. S=(−∞;0)

C. S=(−∞;−1)

D. S=(0;1)

Xem đáp án

Đáp án: C

Giải thích:

Lời giải.

Ta có $x^{2} + x + 1 = {(x + \frac{1}{2})}^{2} + \frac{3}{4} > 0.$

Bất phương trình tương đương với ${(x^{2} + x + 1)}^{x} < {(x^{2} + x + 1)}^{0} . (*)$

Nếu $x^{2} + x + 1 < 1$

$\Leftrightarrow x^{2} + x < 0$

$(*) \Leftrightarrow x > 0$ : không thỏa mãn.

Nếu $x^{2} + x + 1 > 1$

$\Leftrightarrow x^{2} + x > 0$

$(*) \Leftrightarrow x < 0$ .

Kết hợp điều kiện $x < - 1$ .

Vậy bất phương trình có tập nghiệm $S = (- \infty; - 1)$ .

Câu 8:

18/07/2024

Cho bất phương trình $x^{\log_{2} x + 4} \leq 32$ . Mệnh đề nào sau đây đúng?

A. Tập nghiệm của bất phương trình là một khoảng

B. Tập nghiệm của bất phương trình là một đoạn

C. Tập nghiệm của bất phương trình là nửa khoảng

D. Tập nghiệm của bất phương trình là hợp của hai đoạn mà hai đoạn này giao nhau bằng rỗng

Xem đáp án

Đáp án: B

Giải thích:

Lời giải.

Điều kiện: $\log_{2} x = t \overset{}{\to} x = 2^{t}$ .

Bất phương trình

$\Leftrightarrow {(2^{t})}^{t + 4} \leq 32$

$\Leftrightarrow 2^{t (t + 4)} \leq 2^{5}$

$\Leftrightarrow t^{2} + 4 t \leq 5$

$\Leftrightarrow - 5 \leq t \leq 1$

$\overset{}{\to} - 5 \leq \log_{2} x \leq 1$

$\Leftrightarrow \frac{1}{32} \leq x \leq 2$

;2].

Câu 9:

22/07/2024

Gọi a, b là hai nghiệm của bất phương trình $P = a b .$

A. P=e

B. P=1

C. P= $e^{3}$

D. P= $e^{4}$

Xem đáp án

Đáp án: B

Giải thích:

Lời giải.

Điều kiện: $e^{\ln^{2} x} = {(e^{\ln x})}^{\ln x} = x^{\ln x}$ .

Do đó bất phương trình $\Leftrightarrow 2. e^{\ln^{2} x} \leq 2. e^{4}$

$\Leftrightarrow \ln^{2} x \leq 4$

$\Leftrightarrow |\ln x| \leq 2$

$\Leftrightarrow - 2 \leq \ln x \leq 2$

$\Leftrightarrow e^{- 2} \leq x \leq e^{2}$

$\Leftrightarrow \frac{1}{e^{2}} \leq x \leq e^{2}$

$\overset{}{\to} \{\begin{cases} a = \frac{1}{e^{2}} \\ b = e^{2} \end{cases}$

→P=ab=1.

Câu 10:

18/07/2024

Cho hàm số $f (x) = 2^{x} {.7}^{x^{2}}$ . Khẳng định nào sau đây là sai ?

Xem đáp án

Đáp án: D

Giải thích:

Lời giải.

Ta có $f (x) < 1 \Leftrightarrow 2^{x} {.7}^{x^{2}} < 1. (*)$

Lấy logarit cơ số 2 hai vế của (*), ta được $\log_{2} (2^{x} {.7}^{x^{2}}) < \log_{2} 1$

$\Leftrightarrow \log_{2} 2^{x} + \log_{2} 7^{x^{2}} < 0$

$\Leftrightarrow x + x^{2} \log_{2} 7 < 0$ .

Do đó A đúng.

Lấy ln hai vế của (*), ta được $\ln (2^{x} {.7}^{x^{2}}) < \ln 1$

$\Leftrightarrow \ln 2^{x} + \ln 7^{x^{2}} < 0$

$\Leftrightarrow x \ln 2 + x^{2} \ln 7 < 0.$

Do đó B đúng.

Lấy logarit cơ số 7 hai vế của (*), ta được $\log_{7} (2^{x} {.7}^{x^{2}}) < \log_{7} 1$

$\Leftrightarrow \log_{7} 2^{x} + \log_{7} 7^{x^{2}} < 0$

$\Leftrightarrow x \log_{7} 2 + x^{2} < 0$ .

Do đó C đúng.

Vì $x + x^{2} \log_{2} 7 < 0$

$\Leftrightarrow x (1 + x \log_{2} 7) < 0$

$\Leftrightarrow 1 + x \log_{2} 7 < 0$ là sai.

Câu 11:

14/07/2024

Giải bất phương trình $\log_{2} (3 x - 1) > 3$

A. x>3

C. x<3

Xem đáp án

Đáp án: A

Giải thích:

Lời giải.

Bất phương trình $\Leftrightarrow 3 x - 1 > 2^{3}$

$\Leftrightarrow 3 x > 9 \Leftrightarrow x > 3.$

Câu 12:

22/07/2024

Cho bất phương trình $\log_{\frac{1}{3}} (x^{2} - 2 x + 6) \leq - 2$ . Mệnh đề nào sau đây là đúng?

A. Tập nghiệm của bất phương trình là nửa khoảng

B. Tập nghiệm của bất phương trình là một đoạn

C. Tập nghiệm của bất phương trình là hợp của hai nửa khoảng

D. Tập nghiệm của bất phương trình là hợp của hai đoạn

Xem đáp án

Đáp án: C

Giải thích:

Lời giải.

Bất phương trình $\Leftrightarrow - \log_{3} (x^{2} - 2 x + 6) \leq - 2$

$\Leftrightarrow \log_{3} (x^{2} - 2 x + 6) \geq 2$

$\Leftrightarrow x^{2} - 2 x + 6 \geq 9$

$\Leftrightarrow x^{2} - 2 x - 3 \geq 0$

$\Leftrightarrow [\begin{array}{l} x \geq 3 \\ x \leq - 1 \end{array} .$

Vậy bất phương trình có tập nghiệm là $S = (- \infty; - 1] \cup [3; + \infty)$ .

Câu 13:

22/07/2024

Tìm tập nghiệm S của bất phương trình (3x−3).

A. S=(2;+∞)

B. S=(−∞;1)∪(2;+∞)

C. S=(−∞;−1)∪(2;+∞)

D. S=(1;2)

Xem đáp án

Đáp án: A

Giải thích:

Lời giải.

Điều kiện: $\{\begin{cases} x^{2} - 1 > 0 \\ 3 x - 3 > 0 \end{cases} \Leftrightarrow x > 1.$

Bất phương trình: $\log_{\frac{1}{5}} (x^{2} - 1) < \log_{\frac{1}{5}} (3 x - 3)$

$\frac{1}{5} < 1$ )

$\Leftrightarrow x^{2} - 3 x + 2 > 0$

dk:x>1−−−→x>2.

Câu 14:

22/07/2024

Tìm tập nghiệm S của bất phương trình $\frac{9}{4}$ thuộc S

Xem đáp án

Đáp án: A

Giải thích:

Lời giải.

Điều kiện: $\{\begin{cases} x^{2} - x - 2 > 0 \\ - x^{2} + 2 x + 3 > 0 \\ 0 < a \neq 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} 2 < x < 3 \\ 0 < a \neq 1 \end{cases} .$

Do $\log_{a} \frac{13}{16} > \log_{a} \frac{39}{16}$

$\overset{}{\to} 0 < a < 1.$

Vì $\Leftrightarrow x^{2} - x - 2 < - x^{2} + 2 x + 3$

$\Leftrightarrow 2 x^{2} - 3 x - 5 < 0$

$\Leftrightarrow - 1 < x < \frac{5}{2}$

.

Câu 15:

17/07/2024

Tìm tập nghiệm S của bất phương trình

A. S=(2;+∞)

B. S=(1;+∞)

C. S=R\{2}

D. S=(1;+∞)\{2}

Xem đáp án

Đáp án: D

Giải thích:

Lời giải.

Điều kiện: $\{\begin{cases} 4 x - 4 > 0 \\ x \neq 0 \end{cases} \Leftrightarrow x > 1.$

Bất phương trình $\Leftrightarrow x^{2} > 4 x - 4$

$\Leftrightarrow x^{2} - 4 x + 4 > 0$

$\Leftrightarrow {(x - 2)}^{2} > 0$

$\Leftrightarrow x \neq 2$

Đối chiếu điều kiện, ta được tập nghiệm của bpt là $S = (1; + \infty) \ \{2\}$

Câu 16:

13/07/2024

Gọi S là tập nghiệm của bất phương trình $\log_{0, 3} (4 x^{2}) \geq \log_{0, 3} (12 x - 5) .$ Kí hiệu m, M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của tập S. Mệnh đề nào sau đây là đúng?

A. m+M=3

B. m+M=2

C. M−m=3

D. M−m=1

Xem đáp án

Đáp án: A

Giải thích:

Lời giải.

Điều kiện: $x \geq \frac{5}{12} .$

Bất phương trình $\Leftrightarrow 4 x^{2} \leq 12 x - 5$

$\Leftrightarrow 4 x^{2} - 12 x + 5 \leq 0$

$\Leftrightarrow \frac{1}{2} \leq x \leq \frac{5}{2} (t h ỏ a m ã n) .$

Suy ra tập nghiệm của bất phương trình là $S = [\frac{1}{2}; \frac{5}{2}]$ .

Suy ra $m + M = 3.$

Câu 17:

23/07/2024

Tìm tập nghiệm S của bất phương trình

A. S=(3;7)

B. S=(−∞;3)∪(7;+∞)

C. S=(−∞;3)

D. S=(7;+∞)

Xem đáp án

Đáp án: A

Giải thích:

Lời giải.

Điều kiện: x > 0

Bất phương trình

$\Leftrightarrow \log (x^{2} + 21) . \log 10 < \log 10 + \log x$

$\Leftrightarrow \log (x^{2} + 21) < \log (10 x)$

$\Leftrightarrow x^{2} + 21 < 10 x$

$\Leftrightarrow 3 < x < 7 (t h ỏ a m ã n)$

→S=(3;7).

Câu 18:

20/11/2024

Có bao nhiêu số nguyên dương x thỏa mãn bất phương trình $\log (x - 40) + \log (60 - x) < 2$ ?

A. 20

B. 18

C. 21

D. 19

Xem đáp án

Đáp án đúng là: B

Lời giải.

Điều kiện: $40 < x < 60$ .

Bất phương trình $\Leftrightarrow \log [(x - 40) (60 - x)] < 2$

$\Leftrightarrow (x - 40) (60 - x) < 10^{2}$

$\Leftrightarrow x^{2} - 100 x + 2500 > 0$

$\Leftrightarrow {(x - 50)}^{2} > 0 \Leftrightarrow x \neq 50.$

Kết hợp với điều kiện, ta được $\{\begin{cases} 40 < x < 60 \\ x \neq 50 \end{cases}$

$\overset{x \in ℤ^{+}}{\to} x \in \{41; ...; 59\} \ \{50\}$ .

*Phương pháp giải:

Tìm điều kiện

Giải bất phương trình sử dụng tích logarit:

: Với các số dương a, x, y và $a \neq 1$ ta có:

$\log_{a} (x . y) = \log_{a} x + \log_{a} y$

Kết hợp điều kiện suy ra đáp án

*Lý thuyết:

Cho 2 số dương a, b với $a \neq 1$ . Số x thỏa mãn đẳng thức $a^{x} = b$ được gọi là lôgarit cơ số a của b và kí hiệu là $\log_{a} b$

2. Tính chất của Logarit

Với $a, b > 0; a \neq 1$ ta có

$\log_{a} 1 = 0 \log_{a} a = 1 a^{\log_{a} b} = b \log_{a} a^{α} = α . \log_{a} a = α$

Bảng tính chất của Logarit

II. Các quy tắc tính Logarit

1. Lôgarit của một tích

- Định lí 1: Với các số dương a, x, y và $a \neq 1$ ta có:

$\log_{a} (x . y) = \log_{a} x + \log_{a} y$

- Chú ý: Định lí 1 có thể mở rộng cho tích của n số dương:

$\log_{a} (x_{1} . x_{2} ... x_{n}) = \log_{a} x_{1} + \log_{a} x_{2} + ... + \log_{a} x_{n} (a, x_{i}, i = \bar{1, n} > 0; a \neq 1)$

2. Lôgarit của một thương

- Định lí 2: Với các số dương a, x, y và $a \neq 1$ ta có:

$\log_{a} \frac{x}{y} = \log_{a} x - \log_{a} y$

3. Lôgarit của một lũy thừa

- Định lí 3: Lôgarit của một lũy thừa bằng tích của số mũ với lôgarit của cơ số.

$\log_{a} b^{α} = α . \log_{a} b (a, b > 0; a \neq 1, α \in ℝ)$

- Đặc biệt:

$\log_{a} \sqrt[n]{b} = \frac{1}{n} \log_{a} b$

III. Bảng công thức Logarit đầy đủ

1. Công thức Logarit cơ bản

2. Công thức lũy thừa Logarit

3. Công thức đạo hàm Logarit

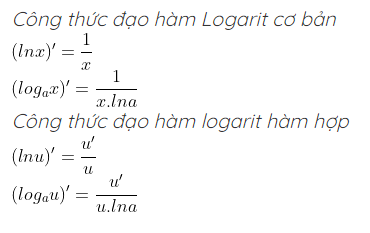
4. Công thức đổi cơ số, lôgarit thập phân và lôgarit tự nhiên

- Cho 3 số dương a, b, c với $a \neq 1, c \neq 1$ , ta có:

$\log_{a} b = \frac{\log_{c} b}{\log_{c} a}$

- Đặc biệt:

$\{\begin{cases} \log_{a} b = \frac{1}{\log_{b} a} (b \neq 1) \\ \log_{a^{α}} b = \frac{1}{α} \log_{a} b (α \neq 0) \end{cases}$

- Lôgarit thập phân: Là lôgarit cơ số 10. Kí hiệu: $\log_{10} x = \log x$

- Lôgarit tự nhiên: Là lôgarit cơ số e. Kí hiệu: $\log_{e} x = \ln x$

- Chú ý: Tìm số các chữ số của một lũy thừa:

Xem thêm

Công thức logarit (2024) đầy đủ, chi tiết nhất

TOP 40 câu Trắc nghiệm Logarit (có đáp án 2024) - Toán 12

Câu 19:

12/07/2024

Biết rằng tập nghiệm của bất phương trình $S = (\frac{1}{a}; b)$ với a, b là những số nguyên. Mệnh đề nào sau đây là đúng?

A. a = -b

B. a + b = 1

C. a = b

D. a = 2b

Xem đáp án

Đáp án: C

Giải thích:

Lời giải.

Điều kiện: $\{\begin{cases} x > 0 \\ 1 + \log_{\frac{1}{9}} x - \log_{9} x > 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} x > 0 \\ 1 - 2 \log_{9} x > 0 \end{cases}$

$\Leftrightarrow [\begin{array}{l} x > 0 \\ \log_{9} x < \frac{1}{2} \end{array}$

$\Leftrightarrow \{\begin{cases} x > 0 \\ x < 3 \end{cases}$

$\Leftrightarrow 0 < x < 3.$

Bất phương trình $\Leftrightarrow 1 - 2 \log_{9} x < 2$

$\Leftrightarrow \log_{9} x > - \frac{1}{2}$

$\Leftrightarrow x > \frac{1}{3} .$

Đối chiếu với điều kiện, ta được tập nghiệm của bất phương trình là $S = (\frac{1}{3}; 3)$ .

Suy ra $a = 3, b = 3$ .

Câu 20:

20/07/2024

Có bao nhiêu giá trị nguyên của x trong đoạn [log2(x+√2x2−x)]<0?

A. 4033

B. 4031

C. 4037

D. 2018

Xem đáp án

Đáp án: B

Giải thích:

Lời giải.

Điều kiện: $\{\begin{cases} \begin{array}{l} x + \sqrt{2 x^{2} - x} > 0 & (1) \end{array} \\ \begin{array}{l} \log_{2} (x + \sqrt{2 x^{2} - x}) > 0 & (2) \end{array} \end{cases}$

Bất phương trình $\log {}_{\frac{π}{4}}{[\log_{2} (x + \sqrt{2 x^{2} - x})]} < \log {}_{\frac{π}{4}}1$

$\Leftrightarrow \log_{2} (x + \sqrt{2 x^{2} - x}) > 1$ (thỏa )

$\Leftrightarrow \log_{2} (x + \sqrt{2 x^{2} - x}) > \log_{2} 2$

$\Leftrightarrow x + \sqrt{2 x^{2} - x} > 2$ (thỏa )

$\Leftrightarrow \sqrt{2 x^{2} - x} > 2 - x$

$\Leftrightarrow [\begin{array}{l} \{\begin{cases} 2 - x < 0 \\ 2 x^{2} - x \geq 0 \end{cases} \\ \{\begin{cases} 2 - x \geq 0 \\ 2 x^{2} - x > {(2 - x)}^{2} \end{cases} \end{array}$

$\Leftrightarrow [\begin{array}{l} x > 1 \\ x < - 4 \end{array}$

có $4031$ giá trị nguyên của x thỏa mãn.

Câu 21:

13/07/2024

Tìm tập nghiệm S của bất phương trình $\log_{2} x + \log_{3} x > 1 + \log_{2} x \log_{3} x .$

A. S=(3;+∞)

B. S=(0;2)∪(3;+∞)

C. S=(2;3)

D. S=(−∞;2)∪(3;+∞)

Xem đáp án

Đáp án: C

Giải thích:

Lời giải.

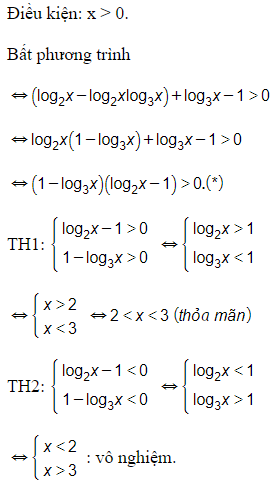
Vậy tập nghiệm của bất phương trình là $S = (2; 3)$ .

Câu 22:

22/07/2024

Có tất cả bao nhiêu số nguyên thỏa mãn bất phương trình $\log {}_{\frac{1}{2}}{[\log_{2} (2 - x^{2})]} > 0$ ?

A. 1

B. 2

C. 3

D. 0

Xem đáp án

Đáp án: D

Giải thích:

Lời giải.

Điều kiện: $\{\begin{cases} 2 - x^{2} > 0 \\ \log_{2} (2 - x^{2}) > 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} 2 - x^{2} > 0 \\ 2 - x^{2} > 1 \end{cases}$

$\Leftrightarrow 2 - x^{2} > 1$

$\Leftrightarrow - 1 < x < 1.$

Bất phương trình $\Leftrightarrow \log {}_{\frac{1}{2}}{[\log_{2} (2 - x^{2})]} > \log {}_{\frac{1}{2}}1$

$\Leftrightarrow \log_{2} (2 - x^{2}) < 1$

$\Leftrightarrow \log_{2} (2 - x^{2}) < \log_{2} 2$

Đối chiếu điều kiện, bất phương trình có tập nghiệm $S = (- 1; 0) \cup (0; 1)$ .

Suy ra không có số nguyên nào thuộc tập S.

Câu 23:

19/07/2024

Tìm tập nghiệm S của bất phương trình )>0

A. S=(−∞;1)∪(4;+∞)

B. S=(−∞;−2)∪(1;+∞)

C. S=(−2;1)∪(1;4)

D. S=(−∞;−2)∪(4;+∞)

Xem đáp án

Đáp án: D

Giải thích:

Lời giải.

Điều kiện: $\{\begin{cases} \frac{2 x + 1}{x - 1} > 0 \\ \log_{3} \frac{2 x + 1}{x - 1} > 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} \frac{2 x + 1}{x - 1} > 0 \\ \frac{2 x + 1}{x - 1} > 1 \end{cases}$

$\Leftrightarrow \frac{2 x + 1}{x - 1} > 1$

$\Leftrightarrow [\begin{array}{l} x > 1 \\ x < - 2 \end{array}$

Bất phương trình $\Leftrightarrow \log_{3} \frac{2 x + 1}{x - 1} < 1$

$\Leftrightarrow \frac{2 x + 1}{x - 1} < 3$

$\Leftrightarrow \frac{4 - x}{x - 1} < 0$

$\Leftrightarrow [\begin{array}{l} x < 1 \\ x > 4 \end{array} .$

Đối chiếu điều kiện, ta được tập nghiệm

Câu 24:

22/07/2024

Tìm tập nghiệm S của bất phương trình ≤12

A. S=(0;2)

B. S=[2;+∞)

C. S=(−∞;2)

D. S=(2;+∞)

Xem đáp án

Đáp án: D

Giải thích:

Lời giải.

Điều kiện: $\{\begin{cases} x > 0 \\ \log_{2} x \neq 1 \end{cases} \Leftrightarrow \{\begin{cases} x > 0 \\ x \neq 2 \end{cases} .$

Bất phương trình $\Leftrightarrow \frac{1 - \frac{1}{2} \log_{2} x}{1 - \log_{2} x} \leq \frac{1}{2}$

$\Leftrightarrow \frac{2 - \log_{2} x}{2 (1 - \log_{2} x)} \leq \frac{1}{2}$

$\Leftrightarrow \frac{2 - \log_{2} x}{1 - \log_{2} x} \leq 1$

$\Leftrightarrow \frac{2 - \log_{2} x}{1 - \log_{2} x} - 1 \leq 0$

$\Leftrightarrow \frac{1}{1 - \log_{2} x} \leq 0$

$\Leftrightarrow 1 - \log_{2} x < 0$

$\Leftrightarrow \log_{2} x > 1$

$\Leftrightarrow x > 2 (t h ỏ a m ã n) .$

Vậy tập nghiệm của bất phương trình là $S = (2; + \infty)$

Câu 25:

15/07/2024

Tìm tất cả các giá trị thực của tham số m để bất phương trình ${(\frac{2}{e})}^{x^{2} + 2 m x + 1} \leq {(\frac{e}{2})}^{2 x - 3 m}$ nghiệm đúng với mọi x

A. m∈(−5;0)

B. m∈[−5;0]

C. m∈(−∞;−5)∪(0;+∞)

D. m∈(−∞;−5]∪[0;+∞)

Xem đáp án

Đáp án: B

Giải thích:

Lời giải.

Bất phương trình $\Leftrightarrow {(\frac{e}{2})}^{- x^{2} - 2 m x - 1} \leq {(\frac{e}{2})}^{2 x - 3 m}$

$\Leftrightarrow - x^{2} - 2 m x - 1 \leq 2 x - 3 m$

Ycbt $\forall x \in ℝ$

$\Leftrightarrow \{\begin{cases} a > 0 \\ Δ' \leq 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} 1 > 0 \\ {(m + 1)}^{2} + 3 m - 1 \leq 0 \end{cases}$

$\Leftrightarrow m^{2} + 5 m \leq 0$

$\Leftrightarrow - 5 \leq m \leq 0.$

Câu 26:

19/07/2024

Tìm tất cả các giá trị thực của tham số để bất phương trình $\log_{2}^{2} x - 2 \log_{2} x + 3 m - 2 < 0$ có nghiệm thực.

A. m<1

B. m≤1

C. m<0

D. m< $\frac{2}{3}$

Xem đáp án

Đáp án: A

Giải thích:

Lời giải.

Điều kiện: x > 0.

Đặt $t \in (- \infty; + \infty)$ .

Bất phương trình đã cho trở thành $t^{2} - 2 t + 3 m - 2 < 0$

$\Leftrightarrow 3 m < - t^{2} + 2 t + 2 (*)$ .

Ycbt $g (t) = - t^{2} + 2 t + 2$ .

Ta có $g (t) = - t^{2} + 2 t + 2$

$= 3 - {(t - 1)}^{2} \leq 3, \forall t \in ℝ$ .

Suy ra $\max_{(- \infty; + \infty)} g (t) = 3$ .

Từ đó suy ra $3 m < 3 \Leftrightarrow m < 1$ thỏa mãn yêu cầu bài toán.

Câu 27:

22/07/2024

Có bao nhiêu giá trị nguyên của tham số m để bất phương trình $\log 5 + \log (x^{2} + 1) \geq \log (m x^{2} + 4 x + m)$ đúng với mọi x?

A. 0.

B. 1

C. 2

D. 4

Xem đáp án

Đáp án: B

Giải thích:

Lời giải.

Để bất phương trình đúng với mọi khi và chỉ khi:

● Bất phương trình xác định với mọi x $\Leftrightarrow m x^{2} + 4 x + m > 0, \forall x \in ℝ$

$\Leftrightarrow \{\begin{cases} m > 0 \\ Δ' < 0 \end{cases}$

$\Leftrightarrow \{\begin{cases} m > 0 \\ 4 - m^{2} < 0 \end{cases}$

$\Leftrightarrow m > 2. (1)$

● Bất phương trình nghiệm đúng với mọi x

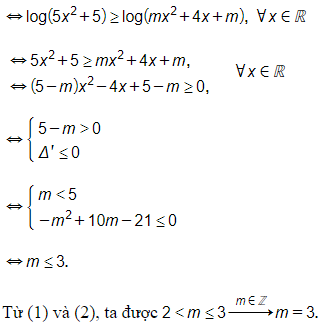
Câu 28:

23/07/2024

Có bao nhiêu giá trị m nguyên thuộc đoạn $\log_{m} (x^{2} + 2 x + m + 1) > 0$ đúng với mọi x?

A. 2015

B. 4030

C. 2016

D. 4032

Xem đáp án

Đáp án: C

Giải thích:

Lời giải.

Để bất phương trình đúng với mọi khi và chỉ khi:

● Bất phương trình xác định với mọi x $\Leftrightarrow \{\begin{cases} x^{2} + 2 x + m + 1 > 0, \forall x \in ℝ \\ 0 < m \neq 1 \end{cases}$

$\Leftrightarrow 0 < m \neq 1.$

● Bất phương trình nghiệm đúng với mọi x $\forall x \in ℝ .$

Nếu m > 1 thì $\forall x \in ℝ$

$\Leftrightarrow Δ' = 1 - m < 0$

$\Leftrightarrow m > 1$ : (thỏa mãn).

Nếu $\forall x \in ℝ$

$\Leftrightarrow \{\begin{cases} 1 < 0 \\ Δ = 1 - m < 0 \end{cases}$ : vô lí.

Vậy m > 1 thỏa mãn yêu cầu bài toán

Lớp 1 - Cánh diều

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Chân trời sáng tạo

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Lớp 1 - Kết nối tri thức

Tiếng Anh 1

Toán lớp 1

Tiếng Việt lớp 1

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 1 lên lớp 2

Giáo án lớp 1

Lớp 2 - Kết nối tri thức

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Lớp 2 - Cánh diều

Toán lớp 2

Tiếng Việt lớp 2

Hoạt động trải nghiệm lớp 2

Tự nhiên và Xã hội lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đạo đức lớp 2

Lớp 2 - Chân trời sáng tạo

Toán lớp 2

Tiếng Việt lớp 2

Đạo đức lớp 2

Tự nhiên và Xã hội lớp 2

Hoạt động trải nghiệm lớp 2

Tiếng Anh lớp 2

Âm nhạc lớp 2

Đề thi các môn lớp 2

Đề thi các môn lớp 2 - Kết nối tri thức

Đề thi các môn lớp 2 - Cánh diều

Đề thi các môn lớp 2 - Chân trời sáng tạo

Tiện ích

Đọc sách online

Bộ đề ôn hè lớp 2 lên lớp 3

Giáo án lớp 2

Lớp 3 - Kết nối tri thức

Toán lớp 3

Tiếng Anh lớp 3

Tiếng Việt lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Cánh diều

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3

Công nghệ lớp 3

Lớp 3 - Chân trời sáng tạo

Toán lớp 3

Tiếng Việt lớp 3

Tiếng Anh lớp 3

Đạo đức lớp 3

Tự nhiên và Xã hội lớp 3

Hoạt động trải nghiệm lớp 3

Âm nhạc lớp 3

Tin học lớp 3

Giáo dục thể chất lớp 3