Có bao nhiêu số nguyên dương x thỏa mãn bất phương trình $\log \left(x-40\right)+\log \left(60-x\right)<2$?

Đáp án đúng là: B

Lời giải.

Điều kiện: $40<x<60$.

Bất phương trình $\iff \log \left[\left(x-40\right)\left(60-x\right)\right]<2$

$\iff \left(x-40\right)\left(60-x\right)<{10}^2$

$\iff x^2-100x+2500>0$

$\iff {\left(x-50\right)}^2>0\iff x\ne 50.$

Kết hợp với điều kiện, ta được $\left\{\begin{array}{l}40<x<60\\ x\ne 50\end{array}\right.$

$\stackrel{x\in {\mathbb{Z}}^{+}}{\to }x\in \left\{41;\mathrm{...};59\right\}\backslash \left\{50\right\}$.

*Phương pháp giải:

Tìm điều kiện

Giải bất phương trình sử dụng tích logarit:

: Với các số dương a, x, y và $a\ne 1$ ta có:

${\log }_a\left(x.y\right)={\log }_{a}x+{\log }_{a}y$

Kết hợp điều kiện suy ra đáp án

*Lý thuyết:

Cho 2 số dương a, b với $a\ne 1$. Số x thỏa mãn đẳng thức $a^x=b$ được gọi là lôgarit cơ số a của b và kí hiệu là ${\log }_{a}b$

2. Tính chất của Logarit

Với $a,b>0;a\ne 1$ ta có

$$\begin{gathered} {\log }_{a}1=0 \\ {\log }_{a}a=1 \\ {a}^{{\log }_{a}b}=b \\ {\log }_a{a}^{\alpha }=\alpha .{\log }_{a}a=\alpha \end{gathered}$$

Bảng tính chất của Logarit

II. Các quy tắc tính Logarit

1. Lôgarit của một tích

- Định lí 1: Với các số dương a, x, y và $a\ne 1$ ta có:

${\log }_a\left(x.y\right)={\log }_{a}x+{\log }_{a}y$

- Chú ý: Định lí 1 có thể mở rộng cho tích của n số dương:

$$\begin{gathered} {\log }_a\left(x_1.x_2\mathrm{...}{x}_n\right) \\ ={\log }_a{x}_1+{\log }_a{x}_2+\mathrm{...}+{\log }_a{x}_n \\ \left(a,x_i,i=\overline{1,n}>0;a\ne 1\right) \end{gathered}$$

2. Lôgarit của một thương

- Định lí 2: Với các số dương a, x, y và $a\ne 1$ ta có:

${\log }_a\frac{x}{y}={\log }_{a}x-{\log }_{a}y$

3. Lôgarit của một lũy thừa

- Định lí 3: Lôgarit của một lũy thừa bằng tích của số mũ với lôgarit của cơ số.

$$\begin{gathered} {\log }_a{b}^{\alpha }=\alpha .{\log }_{a}b \\ \left(a,b>0;a\ne 1,\alpha \in ℝ\right) \end{gathered}$$

- Đặc biệt:

${\log }_a\sqrt[n]{b}=\frac{1}{n}{\log }_{a}b$

III. Bảng công thức Logarit đầy đủ

1. Công thức Logarit cơ bản

2. Công thức lũy thừa Logarit

3. Công thức đạo hàm Logarit

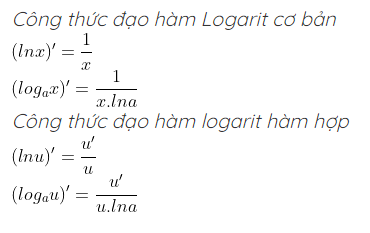
4. Công thức đổi cơ số, lôgarit thập phân và lôgarit tự nhiên

- Cho 3 số dương a, b, c với $a\ne 1,c\ne 1$, ta có:

${\log }_{a}b=\frac{{\log }_{c}b}{{\log }_{c}a}$

- Đặc biệt:

$\left\{\begin{array}{l}{\log }_{a}b=\frac{1}{{\log }_{b}a}\left(b\ne 1\right)\\ {\log }_{a^{\alpha }}b=\frac{1}{\alpha }{\log }_{a}b\left(\alpha \ne 0\right)\end{array}\right.$

- Lôgarit thập phân: Là lôgarit cơ số 10. Kí hiệu: ${\log }_{10}x=\log x$

- Lôgarit tự nhiên: Là lôgarit cơ số e. Kí hiệu: ${\log }_{e}x=\ln x$

- Chú ý: Tìm số các chữ số của một lũy thừa:

Xem thêm

Công thức logarit (2024) đầy đủ, chi tiết nhất 

TOP 40 câu Trắc nghiệm Logarit (có đáp án 2024) - Toán 12