47 câu hỏi trắc nghiệm thuộc Trắc nghiệm Logarit có đáp án

Mệnh đề nào dưới đây sai?

A. $\ln x < 1 \Leftrightarrow 0 < x < e$

B. $\log_{4} x^{2} > \log_{2} y \Leftrightarrow x > y > 0$

C. $\log_{\frac{1}{3}} x < \log_{\frac{1}{3}} y \Leftrightarrow x > y > 0$

D. $\log x > 0 \Leftrightarrow x > 1$

Xem đáp án

Câu 3:

Cho các số thực a, b thỏa mãn 1<a<b, khẳng định nào sau đây là đúng?

A. $\frac{1}{\log_{a} b} < a < \frac{1}{\log_{b} a}$

B. $\frac{1}{\log_{a} b} < \frac{1}{\log_{b} a} < 1$

C. $1 < \frac{1}{\log_{a} b} < \frac{1}{\log_{b} a}$

D. $\frac{1}{\log_{b} a} < 1 < \frac{1}{\log_{a} b}$

Xem đáp án

Câu 4:

14/07/2024

Giá trị $\log_{3} a$ âm khi nào?

A. 0<a<1

B. 0<a<3

C. a>3

D. a>1

Xem đáp án

Câu 5:

19/07/2024

Cho 0<a<1. Chọn khẳng định đúng trong các khẳng định sau

A. Nếu $0 < x_{1} < x_{2}$ thì $\log_{a} x_{1} < \log_{a} x_{2}$

B. Nếu $\log_{a} x < 1$ thì 0<x<a

C. Nếu $\log_{a} x > 0$ thì a>1

D. Nếu $\log_{a} x > \log_{a} x^{2}$ thì x>1

Xem đáp án

Câu 6:

Cho các số thực dương a, b với $a \neq 0$ . Khẳng định nào sau đây là khẳng định đúng?

A. $\log_{a^{2}} (a b) = \frac{1}{2} \log_{a} b$

B. $\log_{a^{2}} (a b) = 2 + \log_{a} b$

C. $\log_{a^{2}} (a b) = \frac{1}{4} \log_{a} b$

D. $\log_{a^{2}} (a b) = \frac{1}{2} + \frac{1}{2} \log_{a} b$

Xem đáp án

Câu 7:

19/07/2024

Với a và b là hai số thực dương tùy ý, $\log (a b^{2})$ bằng

A. $2 \log a + \log b$

B. loga+2logb

C. 2(loga+logb)

D. $\log a + \frac{1}{2} \log b$

Xem đáp án

Câu 8:

Cho $a > 0, a \neq 1, b > 0$ và $\log_{a} b = 2$ . Giá trị của $\log_{a b} (a^{2})$ bằng

A. $\frac{2}{3}$

B. 1

C. $\frac{1}{6}$

D. $\frac{1}{2}$

Xem đáp án

Câu 9:

Với a, b là các số thực dương bất kì, $\log_{2} \frac{a}{b^{2}}$ bằng:

A. $2 \log_{a} \frac{a}{b}$

B. $\frac{1}{2} \log_{2} \frac{a}{b}$

C. $\log_{2} a - 2 \log_{2} b$

D. $\log_{2} a - \log_{2} (2 b)$

Xem đáp án

Câu 10:

Trong các khẳng định dưới đây, khẳng định nào sai?

A. $\log_{0, 5} a > \log_{0, 5} b \Leftrightarrow a > b > 0$

B. $\log x < 0 \Leftrightarrow 0 < x < 1$

C. $\log_{2} x > 0 \Leftrightarrow x > 1$

D. $\log_{\frac{1}{3}} a = \log_{\frac{1}{3}} b \Leftrightarrow a = b > 0$

Xem đáp án

Câu 11:

13/07/2024

Cho hai số thực a và b với 1<a<b. Khẳng định nào dưới đây là khẳng định đúng?

A. $\log_{a} b < 1 < \log_{b} a$

B. $1 < \log_{a} b < \log_{b} a$

C. $\log_{a} b < \log_{b} a < 1$

D. $\log_{b} a < 1 < \log_{a} b$

Xem đáp án

Câu 12:

Đặt $a = \log_{2} 3, b = \log_{5} 3$ . Hãy biểu diễn $\log_{6} 45$ theo a và b

A. $\log_{6} 45 = \frac{2 a^{2} - 2 a b}{a b}$

B. $\log_{6} 45 = \frac{2 a^{2} - 2 a b}{a b + b}$

C. $\log_{6} 45 = \frac{a + 2 b}{a b + b}$

D. $\log_{6} 45 = \frac{a + 2 b}{a b}$

Xem đáp án

Câu 13:

Biết $\log_{15} 20 = a + \frac{2 \log_{3} 2 + b}{\log_{3} 5 + c}$ với $a, b, c \in Z$ . Tính T=a+b+c

A. T=-3

B. T=3

C. T=-1

D. T=1

Xem đáp án

Câu 14:

Nếu $\log 3 = a$ thì log9000 bằng

A. 3+2a

B. $a^{2}$

C. $3 a^{2}$

D. $a^{2} + 3$

Xem đáp án

Câu 15:

Cho $\log_{2} 14 = a$ . Tính $\log_{49} 32$ theo a

A. $\frac{10}{a - 1}$

B. $\frac{2}{5 (a - 1)}$

C. $\frac{5}{2 a - 2}$

D. $\frac{5}{2 a + 1}$

Xem đáp án

Câu 16:

Đặt $\log_{3} 2 = a$ , khi đó $\log_{16} 27$ bằng

A. $\frac{3 a}{4}$

B. $\frac{3}{4 a}$

C. $\frac{4}{3 a}$

D. $\frac{4 a}{3}$

Xem đáp án

Câu 17:

Cho a>0, b>0 thỏa mãn $a^{2} + 4 b^{2} = 5 a b$ A. Khẳng định nào sau đây đúng?

A. 2log(a+2b)=5(loga+logb)

B. log(a+1)+logb=1

C. $\log \frac{a + 2 b}{3} = \frac{\log a + \log b}{2}$

D. $5 \log (a + 2 b) = \log a - \log b$

Xem đáp án

Câu 18:

Với các số $a, b > 0$ thỏa mãn $a^{2} + b^{2} = 6 a b$ , biểu thức $\log_{2} (a + b)$ bằng

A. $\frac{1}{2} (3 + \log_{2} a + \log_{2} b)$

B. $\frac{1}{2} (1 + \log_{2} a + \log_{2} b)$

C. $1 + \frac{1}{2} (\log_{2} a + \log_{2} b)$

D. $2 + \frac{1}{2} (\log_{2} a + \log_{2} b) . g (0)$

Xem đáp án

Câu 19:

Đặt $\log_{2} 60 = a; \log_{5} 15 = b$ . Tính $P = \log_{2} 12$ theo a và b

A. $P = \frac{a b + 2 a + 2}{b}$

B. $P = \frac{a b - a + 2}{b}$

C. $P = \frac{a b + a - 2}{b}$

D. $P = \frac{a b - a - 2}{b}$

Xem đáp án

Câu 20:

Hàm số mũ và hàm số lôgarit | Lý thuyết, công thức, các dạng bài tập và cách giải

Nếu $\log_{a} b = p$ thì $\log_{a} a^{2} b^{4}$ bằng

A. $a^{2} p^{4}$

B. 4p+2

C. 4p+2a

D. $p^{4} + 2 a$

Xem đáp án

Câu 21:

11/11/2024

Cho $\log_{a} x = 2, \log_{b} x = 3$ với a, b là các số thực lớn hơn 1. Tính $P = \log_{\frac{a}{b^{2}}} x$

A. P=6

B. $P = - \frac{1}{6}$

C. P=-6

D. $P = \frac{1}{6}$

Xem đáp án

Đáp án đúng: C

* Lời giải:

* Phương pháp giải:

-Áp dụng các công thức:

- Với các cơ số lôgarit a và b bất kì (0 < a ≠ 1, 0 < b ≠ 1) và M là số thực dương tùy ý ta có:

+) $l {og}_{a} M = \frac{{log}_{b} M}{{log}_{b} a}$ hay logba ⋅ logaM = logbM.

- Định lí 2: Với các số dương a, x, y và a ≠ 1 ta có:

* Lý thuyết cần nắm và dạng toán về logarit:

1. Định nghĩa logarit

Cho hai số dương a; b với a ≠ 1. Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là logab.

$α = \log_{a} b \Leftrightarrow a^{α} = b$

– Chú ý: Không có logarit của số âm và số 0.

2. Tính chất của logarit

Cho hai số dương a và b; a ≠ 1. Ta có các tính chất sau đây:

loga1 = 0; logaa = 1

$a^{\log_{a} b} = b; \log_{a} (a^{α}) = α$

Quy tắc tính logarit

Logarit của một tích

– Định lí 1. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:

$\log_{a} (b_{1} . b {}_{2}) = \log_{a} b_{1} + \log_{a} b {}_{2}$

Logarit của một tích bằng tổng các logarit.

– Chú ý:

Định lí 1 có thể mở rộng cho tích n số dương:

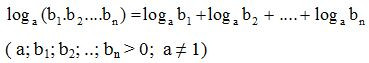
Logarit của một thương

– Định lí 2. Cho ba số dương a; b1 ;b2 với a ≠ 1. Ta có:

$\log_{a} \frac{b_{1}}{b_{2}} = \log_{a} b_{1} - \log_{a} b {}_{2}$

Logarit của một thương bằng hiệu các logarit.

Đặc biệt: $\log_{a} \frac{1}{b} = - \log_{a} b$ ( a > 0; b > 0; a ≠ 1)

Logarit của một lũy thừa

– Định lí 3. Cho hai số dương a; b và a ≠ 1 . Với mọi số α, ta có:

$\log_{a} b^{α} = α \log_{a} b$

Logarit của một lũy thừa bằng tích của số mũ với logarit của cơ số.

– Đặc biệt: $\log_{a} \sqrt[n]{b} = \frac{1}{n} \log_{a} b$

Đổi cơ số logarit

– Định lí 4. Cho ba số dương a; b; c với a ≠ 1; c ≠ 1, ta có:

$\log_{a} b = \frac{\log_{c} b}{\log_{c} a}$

– Đặc biệt:

$\begin{array}{l} \log_{a} b = \frac{1}{\log_{b} a} ( b \neq 1) \\ \log_{a^{α}} b = \frac{1}{α} \log_{a} b (α \neq 0) \end{array}$

Logarit thập phân. Logarit tự nhiên

Logarit thập phân

Logarit thập phân là logarit cơ số 10.

log10b thường được viết là logb hoặc lgb.

Logarit tự nhiên

– Logarit tự nhiên là logarit cơ số e. Logeb được viết là lnb. $\begin{array}{l} \log_{a} b = \frac{1}{\log_{b} a} ( b \neq 1) \\ \log_{a^{α}} b = \frac{1}{α} \log_{a} b (α \neq 0) \end{array}$

Xem thêm các bài viết liên quan hay, chi tiết:

Toán 12 Bài 4: Hàm số mũ. Hàm số lôgarit

50 Bài tập Lôgarit Toán 12 mới nhất

Câu 22:

Cho a là số thực dương khác 1 và b > 0 thỏa mãn $\log_{a} b = \sqrt{3}$ . Tính $A = \log_{a^{2} b} \frac{a}{b^{2}}$ bằng

A. $8 - 5 \sqrt{3}$

B. $\frac{13 - 4 \sqrt{3}}{11}$

C. $5 \sqrt{3} - 8$

D. $\frac{4 \sqrt{3} - 13}{11}$

Xem đáp án

Câu 23:

Cho a, b là các số dương thỏa mãn $\log_{9} a = \log_{16} b = \log_{12} \frac{5 b - a}{2}$ . Tính giá trị $\frac{a}{b}$

A. $\frac{a}{b} = \frac{3 + \sqrt{6}}{4}$

B. $\frac{a}{b} = 7 - 2 \sqrt{6}$

C. $\frac{a}{b} = 7 + 2 \sqrt{6}$

D. $\frac{a}{b} = \frac{3 - \sqrt{6}}{4}$

Xem đáp án

Câu 24:

Đặt $a = \log_{3} 4, b = \log_{5} 4$ . Hãy biểu diễn $\log_{12} 80$ theo a và b

A. $\log_{12} 80 = \frac{2 a^{2} - 2 a b}{a b + b}$

B. $\log_{12} 80 = \frac{a + 2 a b}{a b}$

C. $\log_{12} 80 = \frac{a + 2 a b}{a b + b}$

D. $\log_{12} 80 = \frac{2 a^{2} - 2 a b}{a b}$

Xem đáp án

Câu 25:

Nếu $\log_{12} 6 = a; \log_{12} 7 = b$ thì

A. $\log_{2} 7 = \frac{a}{1 - b}$

B. $\log_{2} 7 = \frac{b}{1 - a}$

D. $\log_{2} 7 = \frac{a}{1 + b}$

D. $\log_{2} 7 = \frac{b}{1 + a}$

Xem đáp án

Gán giá trị đề bài cho bằng cách bấm

Lần lượt thử từng đáp án

Đáp án cần chọn là: B

Câu 26:

20/07/2024

Với mọi a, b, x là các số thực dương thỏa mãn $\log_{2} x = 5 \log_{2} a + 3 \log_{2} b$ . Mệnh đề nào dưới đây là đúng?

A. x=3a+5b

B. x=5a+3b

C. $x = a^{5} + b^{3}$

D. $x = a^{5} b^{3}$

Xem đáp án

Câu 27:

Cho $\log_{3} a = 2$ và $\log_{2} b = \frac{1}{2}$ . Tính giá trị biểu thức $I = 2 \log_{3} [\log_{3} (3 a)] + \log_{\frac{1}{4}} b^{2}$

A. $I = \frac{5}{4}$

B. I=4

C. I=0

D. $I = \frac{3}{2}$

Xem đáp án

Câu 28:

Cho a, b là các số dương khác 1 và thỏa mãn $\log_{a^{2}} b + \log_{b^{2}} a = 1$ . Mệnh đề nào dưới đây đúng?

A. $a = \frac{1}{b}$

B. a=b

C. $a = \frac{1}{b^{2}}$

D. $a = b^{2}$

Xem đáp án

Ta có:

$\log_{a} b . \log_{b} a = 1 \Leftrightarrow \frac{1}{2} (\log_{a} b + \log_{b} a) = 1 \Leftrightarrow \log_{a} b + \log_{b} a = 2$

Vì $\log_{a} b . \log_{b} a = 1$ nên $\log_{a} b, \log_{b} a$ là nghiệm của phương trình $x^{2} - 2 x + 1 = 0$ . Suy ra hay a = b

Đáp án cần chọn là: B

Câu 29:

Gọi m là số chữ số cần dùng khi viết số $2^{30}$ trong hệ thập phân và n là số chữ số cần dùng khi viết số $30^{2}$ trong hệ nhị phân. Ta có tổng m+n bằng:

A. 18

B. 20

C. 19

D. 21

Xem đáp án

Câu 30:

Chọn mệnh đề đúng

A. ln(ab)=lna.lnb

B. $\ln (\frac{a}{b}) = \ln b - \ln a$

C. $\ln a^{n} = n \ln a (a > 0)$

D. lne=e

Xem đáp án

Câu 31:

14/07/2024

Cho các số dương a, b. Chọn mệnh đề đúng:

A. $\ln (a^{n} b) = n \ln a . \ln b$

B. $\ln (\frac{a}{b}) = \frac{\ln a}{\ln b}$

C. $\ln (a b^{n}) = \ln a + n \ln b$

D. $\ln e^{2} = e$

Xem đáp án

Câu 32:

Cho các số thực a<b<0. Mệnh đề nào sau đây sai?

A. $\ln (a b^{2}) = \ln (a^{2}) + \ln (b^{2})$

B. $\ln (\sqrt{a b}) = \frac{1}{2} (\ln a + \ln b)$

C. $\ln (\frac{a}{b}) = \ln |a| - \ln |b|$

D. $\ln {(\frac{a}{b})}^{2} = \ln (a^{2}) - \ln (b^{2})$

Xem đáp án

Do a<b<0 nên đáp án B viết lna, lnb là sai

Đáp án cần chọn là: B

Câu 33:

Cho các số thực dương a, b, x, y với $a \neq 1, b \neq 1$ . Khẳng định nào sau đây là khẳng định sai?

A. $\log_{a} b . \log_{b} a = 1$

B. $\ln \frac{x}{\sqrt{y}} = \ln x - \frac{1}{2} \ln y$

C. $\log_{a} x + \log_{\sqrt[3]{a}} y = \log_{a} (x y^{3})$

D. $\log_{a} (x + y) = \log_{a} x + \log_{a} y$

Xem đáp án

Câu 34:

18/07/2024

Cho các số dương a, b, c. Biểu thức $S = \ln \frac{a}{b} + \ln \frac{b}{c} + \ln \frac{c}{d} + \ln \frac{d}{a}$ bằng:

A. 0

B. 1

C. $\ln (\frac{a}{b} + \frac{b}{c} + \frac{c}{d} + \frac{d}{a})$

D. ln(abcd)

Xem đáp án

Câu 35:

Khẳng định nào sau đây là sai?

A. $\log_{3} x < 0 \Leftrightarrow 0 < x < 1$

B. $\log_{\frac{1}{3}} a > \log_{\frac{1}{3}} b \Leftrightarrow 0 < a < b$

C. $\ln x > 0 \Leftrightarrow x > 1$

D. $\log_{\frac{1}{2}} a > \log_{\frac{1}{2}} b \Leftrightarrow a = b > 0$

Xem đáp án

Câu 36:

Cho a, b, c là các số thực dương thỏa mãn $a^{2} = b c$ . Tính $S = 2 \ln a - \ln b - \ln c$

A. $S = 2 \ln (\frac{a}{b c})$

B. S=1

C. S=-2

D. S=0

Xem đáp án

Câu 37:

Cho các phát biểu sau

(I): Nếu $C = \sqrt{A B}$ thì 2lnC=lnA+lnB với A, B là các biểu thức luôn nhận giá trị dương

(II): $(a - 1) \log_{a} x \geq 0 \Leftrightarrow x \geq 1$ với a>0, $a \neq 1$

(III): $m^{\log_{a} m} = n^{\log_{a} n}$ , với m,n>0; a>0, $a \neq 1$

(IV): $\lim_{x \to + \infty} \log_{\frac{1}{2}} x = - \infty$

Số phát biểu đúng là

A. 4

B. 2

C. 3

D. 1

Xem đáp án

Loagarit cơ só m hai vế ta được $\log_{a} m . \log_{m} n \neq \log_{a} n . \log_{m} n$ suy ra III sai.

Ta có:

$\lim_{x \to + \infty} \log_{\frac{1}{2}} x = - \infty$ đúng nên IV đúng

Vậy có 3 phát biểu đúng

Đáp án cần chọn là: C

Câu 38:

Cho các mệnh đề sau:

(I). Cơ số của logarit là số nguyên dương

(II). Chỉ số thực dương mới có logarit

(III). ln(A+B)=lnA+lnB với mọi A>0, B>0

(IV). $\log_{a} b . \log_{b} c . \log_{c} a = 1$ với mọi $a, b, c \in R$

Số mệnh đề đúng là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Cơ số của logarit phải là số dương khác 1. Do đó (I) sai

Rõ ràng (II) đúng theo điều kiện xác định của $\log_{a} b$ là b > 0.

Ta có: ln(A+B)=ln(A.B) với mọi A > 0, B > 0. Do đó (III) sai.

Ta có: $\log_{a} b . \log_{b} c . \log_{c} a = 1$ với mọi $0 < a, c \neq 1$ . Do đó (IV) sai.

Vậy chỉ có 1 mệnh đề đúng.

Đáp án cần chọn là: A

Câu 39:

Cho logx=a và ln10=b. Tính $\log_{10 e} x$ theo a và b

A. $\frac{2 a b}{1 + b}$

B. $\frac{a b}{1 + b}$

C. $\frac{a}{1 + b}$

D. $\frac{b}{1 + b}$

Xem đáp án

Câu 40:

Tính $P = \ln (2 \cos 1 °) . \ln (2 \cos 2 °)$ $. \ln (2 \cos 3 °) . . . (2 \cos 89 °)$ , biết rằng trong tích đã cho có 89 thừa số có dạng $\ln (2 \cos a °)$ với $1 \leq a \leq 89$ và $a \in Z$

A. P=1

B. P=-1

C. $P = \frac{2^{89}}{89!}$

D. P=0

Xem đáp án

Câu 41:

Công thức nào sau đây là công thức tăng trưởng mũ?

A. $T = A . e^{N r}$

B. $T = N . e^{A r}$

C. $T = r . e^{N A}$

D. $T = A . e^{N - r}$

Xem đáp án

Công thức lãi kép (hoặc công thức tăng trưởng mũ)

$T = A . e^{N r}$ , ở đó A là số tiền gửi ban đầu, r là lãi suất, N là số kì hạn.

Đáp án cần chọn là: A

Câu 42:

Một quần thể sinh vật tại thời điểm hiện tại có T (con), biết quần thể đó có tỉ lệ tăng trưởng r theo năm, hỏi số sinh vật trong quần thể từ 2 năm trước là bao nhiêu?

A. $A = T e^{2 r}$

B. $A = T e^{- 2 r}$

C. $A = \frac{T}{e^{- 2 r}}$

D. $A = 2 T e^{- r}$

Xem đáp án

Từ công thức tăng trưởng mũ: $T = A . e^{N r}$ với N = 2 ta được: $A = \frac{T}{e^{2 r}} = T . e^{- 2 r}$

Đáp án cần chọn là: B

Câu 43:

Khi ánh sáng đi qua một môi trường (chẳng hạn như không khí, nước, sương mù…) cường độ sẽ giảm dần theo quãng đường truyền x, theo công thức $I (x) = I_{0} e^{- μ x}$ , trong đó $I_{0}$ là cường độ của ánh sáng khi bắt đầu truyền vào môi trường và $μ$ là hệ số hấp thụ của môi trường đó. Biết rằng nước biển có hệ số hấp thu $μ = 1, 4$ và người ta tính được rằng khi đi từ độ sâu 2m xuống đến độ sâu 20m thì cường độ ánh sáng giảm $L . 10^{10}$ lần. Số nguyên nào sau đây gần với L nhất?

A. 8

B. 10

C. 9

D. 90

Xem đáp án

Câu 44:

Cường độ ánh sáng đi qua môi trường nước biển giảm dần theo công thức $I = I_{0} . e^{- μ x}$ , với $I_{0}$ là cường độ ánh sáng bắt đầu đi vào môi trường nước biển và x là độ dày của môi trường đó (tính theo đơn vị mét). Biết rằng môi trường nước biển có hằng số hấp thụ là $μ = 1, 4$ . Hỏi ở độ sâu 30 mét thì cường độ ánh sáng giảm đi bao nhiêu lần so với nường độ ánh sáng lúc ánh sáng bắt đầu đi vào nước biển?

A. $e^{- 21} l ầ n$

B. $e^{42} l ầ n$

C. $e^{21} l ầ n$

D. $e^{- 42} l ầ n$

Xem đáp án

Cường độ ánh sáng ở độ sâu 30m là: $I_{1} = I_{0} . e^{- 30 μ}$

Cường độ ánh sáng lúc ánh sáng bắt đầu đi vào nước biển là $I_{2} = I_{0}$

Ta có:

Vậy ở độ sâu 30 mét thì cường độ ánh sáng giảm đi $e^{42}$ lần so với cường độ ánh sáng lúc ánh sáng bắt đầu đi vào nước biển.

Đáp án cần chọn là: B

Câu 45:

Một điện thoại đang nạp pin, dung lượng pin nạp được tính theo công thức $Q (t) = Q_{0} (1 - e^{- t \sqrt{2}})$ với t là khoảng thời gian tính bằng giờ và $Q_{0}$ là dung lượng nạp tối đa (pin đầy). Hãy tính thời gian nạp pin của điện thoại tính từ lúc cạn hết pin cho đến khi điện thoại đạt được 90% dung lượng pin tối đa (kết quả được làm tròn đến hàng phần trăm)

A. $t \approx 1, 65 g i ờ$

B. $t \approx 1, 61 g i ờ$

C. $t \approx 1, 63 g i ờ$

D. $t \approx 1, 50 g i ờ$

Xem đáp án

Câu 46:

Các khí thải gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng lên. Theo OECD (Tổ chức hợp tác và phát triển kinh tế thế giới), khi nhiệt độ trái đất tăng lên thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính rằng khi nhiệt độ trái đất tăng thêm $2 ° C$ thì tổng giá trị kinh tế toàn cầu giảm 3%, còn khi nhiệt độ trái đất tăng thêm $5 ° C$ thì tổng giá trị kinh tế toàn càu giảm 10%. Biết rằng nếu nhiệt độ trái đất tăng thêm $t ° C$ , tổng giá trị kinh tế toàn cầu giảm $f (t) = k . a^{t}$ (trong đó a, k là các hằng số dương). Nhiệt độ trái đất tăng thêm bao nhiêu độ C thì tổng giá trị kinh tế toàn cầu giảm ?

A. $9, 3 ° C$

B. $7, 6 ° C$

C. $6, 7 ° C$

D. $8, 4 ° C$

Xem đáp án

Câu 47: