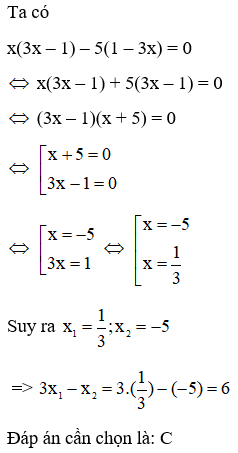Trắc nghiệm Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung (có đáp án)
Trắc nghiệm Toán 8 Bài 6: Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
-
366 lượt thi
-
24 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Chọn câu sai.
Xem đáp án
+) Đáp án A:
(x – 2)2 – (2 – x)3= (x – 2)2 + (x – 2)3
= (x – 2)2(1 + x – 2)
= (x – 2)2(x – 1) nên A đúng.
+) Đáp án B:
(x – 2)2 – (2 – x)
= (x – 2)2 + (x – 2)
= (x – 2)(x – 2 + 1)
= (x – 2)(x – 1)
Nên B đúng
+) Đáp án C:
(x – 2)3 – (2 – x)2
= (x – 2)3 - (x – 2)2
= (x – 2)2(x – 2 – 1)
= (x – 2)2(x – 3) nên C sai.
+) Đáp án D:
(x – 2)2 + x – 2
= (x – 2)(x – 2) + (x – 2)
= (x – 2)(x – 2 + 1)
= (x – 2)(x – 1)
Nên D đúng
Đáp án cần chọn là: C
Câu 2:
16/07/2024Nhân tử chung của
biểu thức 30(4 – 2x)2 + 3x – 6 có thể là
Xem đáp án
Ta có
30(4 – 2x)2 + 3x – 6
= 30(2x – 4)2 + 3(x – 2)
= 30.22(x – 2)2 + 3(x – 2)
= 120(x – 2)2 + 3(x – 2)
= 3(x – 2)(40(x – 2) + 1)
= 3(x – 2)(40x – 79)
Nhân tử chung có thể là 3(x – 2)
Đáp án cần chọn là: B
Câu 3:
23/07/2024Cho ab(x – 5) – a2(5 – x) = a(x – 5)(…).
Điền biểu thức thích hợp vào dấu …
Xem đáp án
ab(x – 5) – a2(5 – x)
= ab(x – 5) + a2(x – 5)
= (x – 5)(ab + a2)
= a(x – 5)(a + b)
Biểu thức cần điền vào dấu … là a + b
Đáp án cần chọn là: D
Câu 4:
18/07/2024Phân tích đa thức 3x(x – 3y) + 9y(3y – x)
thành nhân tử ta được
Xem đáp án
Ta có
3x(x – 3y) + 9y(3y – x)
= 3x(x – 3y) – 9y(x – 3y)
= (x – 3y)(3x – 9y)
= (x – 3y).3(x – 3y)
= 3(x – 3y)2
Đáp án cần chọn là: A
Câu 5:
16/07/2024Cho B = 85 – 211.
Khi đó B chia hết cho số nào dưới đây?
Xem đáp án
Ta có
B = 85 – 211 = (23)5 – 211
= 215 – 211 = 211.24 – 211
= 211(24 – 1) = 15.211
Vì 15 ⁝ 15
=> B = 15.211 ⁝ 15
Đáp án cần chọn là: C
Câu 6:
16/07/2024 Xem đáp án
Ta có
5x(x – y) – (y – x)
= 5x(x – y) + (x – y)
= (x – y)(5x + 1)
Đáp án cần chọn là: A
Câu 7:
18/07/2024Cho 3a2(x + 1) – 4bx – 4b = (x + 1)(…).
Điền biểu thức thích hợp vào dấu
Xem đáp án
3a2(x + 1) – 4bx – 4b
= 3a2(x + 1) – (4bx + 4b)
= 3a2(x + 1) – 4b(x + 1)
= (x + 1)(3a2 – 4b)
Vậy ta điền vào dấu … biểu thức 3a2 – 4b
Đáp án cần chọn là: C
Câu 8:
16/07/2024Cho 2992 + 299.201.
Khi đó tổng trên chia hết cho số nào dưới đây?
Xem đáp án
Ta có
2992 + 299.201
= 299.(299 + 201)
= 299.500 ⁝ 500
Đáp án cần chọn là: A
Câu 9:
20/07/2024Cho 4xn+2 – 8xn (n Є N*).
Khi đặt nhân tử chung xn ra ngoài thì nhân tử còn lại là
Xem đáp án
Ta có
4xn+2 – 8xn = 4xn.x2 – 8xn
= xn(4x2 – 8)
Vậy khi đặt nhân tử chung xn ra ngoài
ta được biểu thức còn lại là 4x2 – 8
Đáp án cần chọn là: B
Câu 10:
16/07/2024Cho A = 2019n+1 – 2019n.
Khi đó A chia hết cho số nào dưới đây với mọi n N
Xem đáp án
Ta có
A = 2019n+1 – 2019n
= 2019n.2019 – 2019n
= 2019n(2019 – 1)
= 2019n.2018
Vì 2018 ⁝ 2018 => A ⁝ 2018 với mọi n N.
Đáp án cần chọn là: B
Câu 13:
17/07/2024Cho x0 là giá trị lớn nhất
thỏa mãn 25x4 – x2 = 0. Chọn câu đúng
Xem đáp án
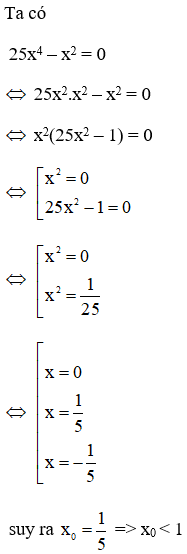
Đáp án cần chọn là: A
Câu 14:
23/07/2024Cho (a – b)(a + 2b) – (b – a)(2a – b) – (a – b)(a + 3b).
Khi đặt nhân tử chung (a – b) ra ngoài thì nhân tử còn lại là
Xem đáp án
Ta có
(a – b)(a + 2b) – (b – a)(2a – b) – (a – b)(a + 3b)
= (a – b)(a + 2b) + (a – b)(2a – b) – (a – b)(a + 3b)
= (a – b)(a + 2b + 2a – b – (a + 3b))
= (a – b)(3a + b – a – 3b)
= (a – b)(2a – 2b)
Vậy khi đặt nhân tử chung (a – b) ra ngoài ta được biểu thức còn lại là 2a – 2b.
Đáp án cần chọn là: A
Câu 16:
17/07/2024Có bao nhiêu giá trị x
thỏa mãn x2(x – 2) = 3x(x – 2)
Xem đáp án
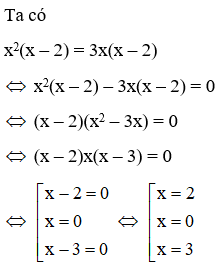
Vậy có 3 giá trị x thỏa mãn điều kiện đề bài x = 2; x = 0; x = 3.
Đáp án cần chọn là: C
Câu 18:
16/07/2024Cho 2992 + 299.201.
Khi đó tổng trên chia hết cho số nào dưới đây?
Xem đáp án
Ta có
2992 + 299.201
= 299.(299 + 201)
= 299.500 ⁝ 500
Đáp án cần chọn là: A
Câu 21:
18/07/2024Phân tích đa thức
7x2y2 – 21xy2z + 7xyz + 14xy ta được
Xem đáp án
Ta có
7x2y2 – 21xy2z + 7xyz + 14xy
= 7xy.xy – 7xy.3yz + 7xy.z + 7xy.2
= 7xy(xy – 3yz + z + 2)
Đáp án cần chọn là: D
Câu 22:
21/07/2024 Xem đáp án
Ta có
12x3y – 6xy + 3xy2
= 3xy.4x2 – 3xy.2 + 3xy.y
= 3xy(4x2 – 2 + y)
Đáp án cần chọn là: A
Câu 23:
21/07/2024Phân tích đa thức
mx + my + m thành nhân tử ta được
Xem đáp án
Ta có mx + my + m
= m(x + y + 1)
Đáp án cần chọn là: A
Câu 24:
21/07/2024 Xem đáp án
Ta có
+) (x – 1)3 + 2(x – 1)2
= (x – 1)2(x – 1) + 2(x – 1)2
= (x – 1)2(x – 1 + 2)
= (x – 1)2(x + 1) nên A đúng
+) (x – 1)3 + 2(x – 1)
= (x – 1).(x – 1)2 + 2(x – 1)
= (x – 1)[(x – 1)2 + 2] nên B đúng
+) (x – 1)3 + 2(x – 1)2
= (x – 1)(x – 1)2 + 2(x – 1)(x – 1)
= (x – 1)[(x – 1)2 + 2(x – 1)]
= (x – 1)[(x – 1)2 + 2x – 2] nên C đúng
+) (x – 1)3 + 2(x – 1)2
= (x – 1)2(x + 1)
≠ (x – 1)(x + 3) nên D sai
Đáp án cần chọn là: D