Trắc nghiệm Toán 12 Bài 2: Mặt cầu
-
467 lượt thi
-
28 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
11/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
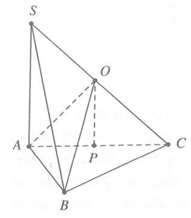
Gọi P là tâm đường tròn ngoại tiếp ΔABC. Trục đường tròn ngoại tiếp ΔABC cắt SC tại O.
Ta có {OA=OB=OCOC=OS
⇒OA=OB=OC=OS.
Vậy O là tâm mặt cầu qua các điểm S, A, B, C
Câu 2:
15/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
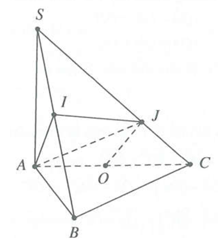
Gọi O là trung điểm của AC.
Ta có:
{AB⊥BC⇒OA=OC=OBAJ=JC⇒OA=OC=OJ
Từ {BC⊥ABBC⊥SA
⇒BC⊥(SAB)⇔BC⊥AI.
Mà AI⊥SB
⇒AI⊥(SBC)⇒AI⊥IC
⇒OA=OC=OI
⇒OA=OB=OC=OI=OJ.
Vậy O là tâm mặt cầu cần tìm.
Câu 3:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
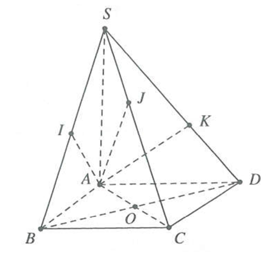
Gọi O là tâm của hình vuông ABCD.
Ta có {BC⊥ABBC⊥SA
⇒BC⊥(SAB)⇒BC⊥AI.
AI⊥SB⇒AI⊥(SBC)
⇒AI⊥IC⇒OA=OC=OI.
Tương tự OA=OC=OK.
Mà AJ⊥SC⇒OA=OC=OJ
⇒OA=OB=OC
=OD=OI=OJ=OK
⇒O là tâm mặt cầu cần tìm.
Câu 4:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
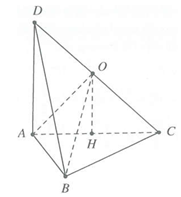
Gọi O là trung điểm của CD.
Ta có OA=OB=OC=OD
=R=12CD.
Cạnh CD=√AD2+AC2
=√AD2+AB2+BC2
=5a√2
R=5a√2.
Câu 5:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
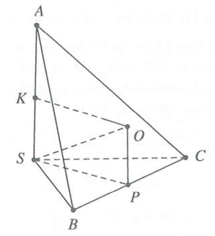
Ta có {SA⊥SBSA⊥SC⇒SA⊥(SBC).
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp tam giác SBC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có R=OS=√OP2+SP2.
OP=SK=SA2=a2;
SP=12BC=12√b2+c2
R=12√a2+b2+c2.
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Ta có {SA⊥SBSA⊥SC⇒SA⊥(SBC).
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp tam giác SBC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có R=OS=√OP2+SP2.
OP=SK=SA2=a;
SP=12BC
=12√SB2+SC2
=a√5
R=a√6.
Câu 7:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
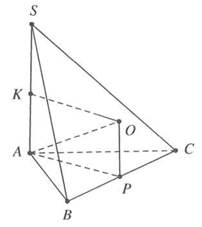
Kí hiệu các điểm như hình vẽ với OP là trục đường tròn ngoại tiếp tam giác ABC và OK là trung trực của SA thì O là tâm mặt cầu.
Ta có R=OA=√OP2+AP2
OP=AK=SA2=√14;
AP=12BC
=12√32+42=52
⇒R=92
⇒V=43πR3=2432π.
Câu 8:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Đặt R1=RABCD;
R2=RSAB,
AB=(SAB)∩(ABC)
Tam giác ABDC là hình vuông cạnh bằng 2a nên
R1=AC2=2a√22=a√2.
Tam giác SAB vuông cân tại S nên
R2=AB2=a.
Do (SAB)⊥(ABC)
nên r=RS.ABC
=√R21+R22−AB24=a√2.
Câu 9:
11/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
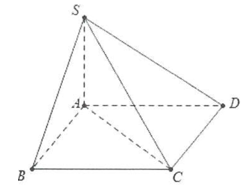
Do SA⊥(ABCD)
⇒(^SC;(ABCD))=^SCA=450.
Ta có:
AC=√AB2+AD2=a√5
⇒SA=ACtan450=a√5.
Lại có: Rd=RABCD=AC2=a√52.
Do SA⊥(ABCD)
⇒R=√SA24+R2d
=a√102.
Thể tích khối cầu ngoại tiếp hình chóp S.ABCD là:
V=43πR3=5√10πa33.
Câu 10:
11/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
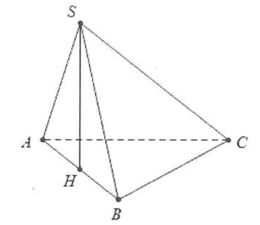
Gọi H là trung điểm của AB.
Do SA=SB⇒SH⊥AB.
Ta có: SB2+BC2=SC2=5a2
⇒SB⊥BC
Mặt khác: AB⊥BC
⇒BC⊥(SAB)⇒BC⊥SH
Suy ra SH⊥(ABC),
đặt R1=RABC=AC2=a.
Đặt R2=RSAB=SA.SB.AB4SSAB
=SA.SB.AB2.SH.AB=SA.SB2SH
=a2SH
Trong đó:
SH=√SB2−HB2
=a√72
⇒R2=2a√7
Suy ra:
RS.ABC=√R21+R22−AB24
=a√25914.
Câu 11:
14/07/2024 Xem đáp án
Xem đáp án
Câu 12:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Chọn C vì cạnh bên đồng phẳng với trục và đáy là tứ giác nội tiếp thì thì hình chóp tứ giác mới có tâm mặt cầu ngoại tiếp.
Câu 13:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có giao tuyến của mặt phẳng (P) với mặt cầu là một đường tròn. Khi đó A, B, C nằm trên đường tròn này, nếu để ý kĩ ta thấy CA2=AB2+BC2, do vậy tam giác ABC vuông tại B, tức là AC chính là đường kính của đường tròn này, hay r=15 dm. Ta có hình vẽ minh họa sau:
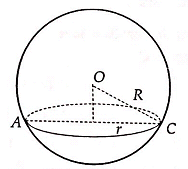
Nhìn vào hình vẽ ta thấy:
d(O;(P))=√R2−r2
=√172−152=8
Câu 14:
15/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng: B
*Lời giải:
Mặt cầu ngoại tiếp hình lập phương có bán kính
mà
Vậy
*Phương pháp giải:
- Tính bán kính khối cầu
- Áp dụng công thức tính thể tích khối cầu để tính:
*Một số dạng bài và lý thuyết thêm về khối cầu:
Diện tích mặt cầu và thể tích khối cầu
Cho mặt cầu S(I; R).
Diện tích mặt cầu:
Thể tích khối cầu:
Dạng 1: Mặt cầu ngoại tiếp hình chóp
* Phương pháp giải:
- Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).
- Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục ∆ của đường tròn ngoại tiếp một đa giác của mặt bên).
- Giao điểm I của (P) và d (hoặc của ∆ và d) là tâm mặt cầu ngoại tiếp.
- Kết luận: I là tâm mặt cầu ngoại tiếp chóp.
Dạng 1.1: Hình chóp có các điểm cùng nhìn một cạnh của hình chóp dưới một góc vuông.
+) Hình chóp tam giác:
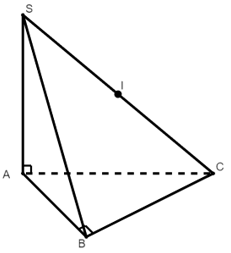
A, B cùng nhìn SC dưới một góc vuông
Tâm mặt cầu ngoại tiếp hình chóp S.ABC là trung điểm I của SC
Bán kính là:
+) Hình chóp tứ giác
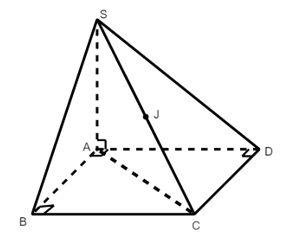
A, B, D cùng nhìn SC dưới một góc vuông
Tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm J của SC
Bán kính mặt cầu là:
Dạng 1.2: Hình chóp có mặt bên vuông góc với mặt phẳng đáy
* Phương pháp giải: Gọi h là chiều cao hình chóp và là bán kính của đường tròn ngoại tiếp mặt bên, mặt đáy và là độ dài cạnh chung của mặt bên vuông góc với đáy thì bán kính mặt cầu là:
Dạng 1.3: Mặt cầu nội tiếp khối đa diện
* Phương pháp giải: Nếu đặt V là thể tích khối chóp và là tổng diện tích mặt đáy và các mặt bên của chóp thì bán kính r của mặt cầu nội tiếp khối chóp:
Xem thêm các bài viết liên quan hay, chi tiết
Các bài toán thực tế hình không gian (có đáp án)
Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)
Câu 15:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Gọi lần lượt là trung trung điểm Theo tính chất hình bình hành ta chứng minh được cắt nhau tại trung điểm của mỗi đường, gọi giao điểm là O.
Vì ABCD là tứ diện đều
và
O là tâm mặt cầu tiếp xúc với các cạnh tứ diện ABCD
Xét hình vuông IJKH cạnh
.
Câu 16:
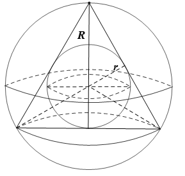
20/07/2024Một hình nón có thiết diện qua trục là tam giác đều. Tỉ số thể tích của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón là:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Giả sử đường sinh hình nón có độ dài là a. Gọi G là trọng tâm của tam giác thiết diện, do đó G cách đều 3 đỉnh và 3 cạnh của tam giác thiết diện, nên G là tâm của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón, suy ra bán kính R, r của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón, suy ra bán kính R, r của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón lần lượt là . Gọi , lần lượt là thể tích của khối cầu ngoại tiếp và khối cầu nội tiếp khối nón. Vậy .
Câu 17:
19/07/2024Có một hộp nhựa hình lập phương người ta bỏ vào hộp đó 1 quả bóng đá. Tính tỉ số , trong đó V1 là tổng thế tích của quả bóng đá, V2 là thể tích của chiếc hộp đựng bóng. Biết rằng đường tròn lớn trên quả bóng có thể nội tiếp 1 mặt hình vuông của chiếc hộp.

 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Gọi R là bán kính của mặt cầu, khi đó cạnh của hình lập phương là 2R
Ta được: Thể tích hình lập phương là , thể tích quả bóng là:
Câu 18:
23/07/2024Một khối cầu nội tiếp trong hình lập phương có đường chéo bằng . Thể tích của khối cầu là:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
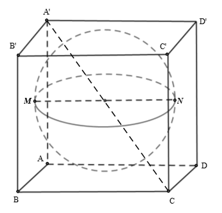
Cho các đỉnh A, B, C, D, A’, B’, C’, D’ như hình vẽ và gọi M, N là tâm các hình vuông ABB’A’ và ADD’C’
Gọi a là độ dài cạnh của hình lập phương.
Ta có:
bán kính khối cầu
Thể tích khối cầu là:
Câu 19:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
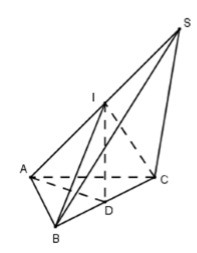
Gọi I là trung điểm của SA
Vì tam giác SAB vuông tại B nên
Vì tam giác SAC vuông tại C nên
Do đó nên I là tâm mặt cầu ngoại tiếp khối chóp S.ABC.
Gọi D là trung điểm của BC ta có D là tâm đường tròn ngoại tiếp tam giác ABC
Câu 20:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
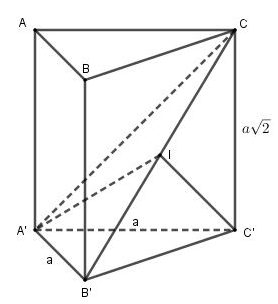
Ta có:
vuông tại A’.
Gọi I là trung điểm của B’C thì
Mà vuông tại C’ nên
Vậy I là tâm mặt cầu ngoại tiếp tứ diện CA’B’C’ và bán kính
Câu 21:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Ta thấy:
Khi đó chu vi đường tròn bằng
Câu 22:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Áp dụng công thức ta có:
Câu 23:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Thể tích khối cầu có bán kính là:
Thể tích khối cầu có bán kính R = 2a là:
Câu 24:
17/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
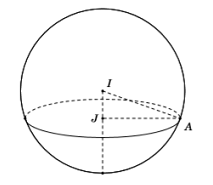
Gọi I, J theo thứ tự là tâm mặt cầu (S) và đường tròn (T), A là điểm bất kì thuộc đường tròn (T). Khi đó ta có:
Áp dụng định lí Pitago trong tam giác vuông AIJ ta có:
Bán kính của mặt cầu là
Vậy diện tích mặt cầu (S) là:
Câu 25:
09/11/2024 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải:
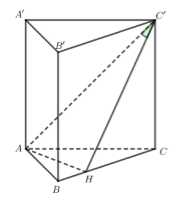
Trong mặt phẳng (ABC) kẻ
Lại có
(do
Ta có:
Gọi R là bán kính mặt cầu ngoại tiếp lăng trụ, khi đó với là bán kính đường tròn ngoại tiếp tam giác vuông ABC và
Do đó
*Phương pháp giải:
Dựng hình tìm tâm mặt cầu ngoại tiếp
*Lý thuyết:
- Tập hợp những điểm M trong không gian cách điểm O cố định một khoảng không đổi bằng r (r > 0) được gọi là mặt cầu tâm O, bán kính r.
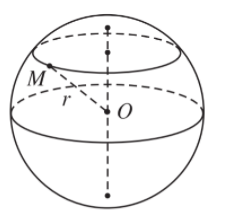
Ta kí hiệu mặt cầu tâm O, bán kính r là S(O; r) hay viết tắt là (S). Như vậy ta có mặt cầu S(O; r) = {M| OM = r}.
- Nếu hai điểm C; D nằm trên mặt cầu S(O; r) thì đoạn thẳng CD được gọi là dây cung của mặt cầu đó.
- Dây cung AB đi qua tâm O được gọi là một đường kính của mặt cầu. Khi đó, độ dài đường kính bằng 2r.
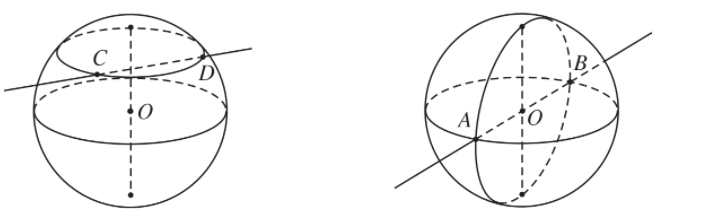
- Một mặt cầu được xác định nếu biết tâm và bán kính của nó hoặc biết một đường kính của mặt cầu đó.
Xem thêm
Câu 26:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Bán kính khối cầu ngoại tiếp hình hộp:
Thể tích khối cầu:
Câu 27:
15/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Áp dụng các công thức trong tứ diện đều cạnh a
Bán kính mặt cầu nội tiếp
Thể tích tứ diện đều đó là:
Câu 28:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
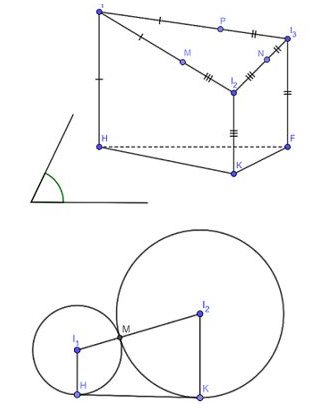
Gọi là tâm của các hình cầu M, N, P là các tiếp điểm của các hình cầu (như hình vẽ), H, K, F là tiếp ba hình cầu với mặt phẳng (P)
Xét mặt phẳng có:
Tương tự:
Vậy
Có thể bạn quan tâm
- Trắc nghiệm Mặt cầu (có đáp án) (466 lượt thi)
- 32 câu trắc nghiệm: Mặt cầu có đáp án (333 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (Nhận biết) (327 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (Thông hiểu) (393 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (Vận dụng) (370 lượt thi)
- Trắc nghiệm Mặt cầu có đáp án (334 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Thông hiểu) (700 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay (có đáp án) (550 lượt thi)
- 52 câu trắc nghiệm: Khái niệm về mặt tròn xoay có đáp án (456 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Vận dụng) (387 lượt thi)
- Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án (384 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án (Nhận biết) (371 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Thông hiểu) (351 lượt thi)
- Trắc nghiệm Khái niệm về mặt tròn xoay có đáp án - Phần 2 (Nhận biết) (347 lượt thi)
- Trắc nghiệm Ôn tập Toán 12 Chương 2: Hình học (có đáp án) (346 lượt thi)
- Trắc nghiệm Ôn tập chương II Hình học 12 có đáp án (Nhận biết) (345 lượt thi)
