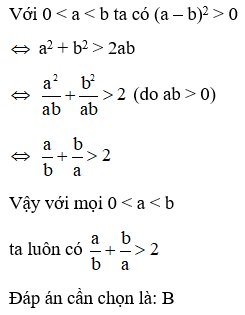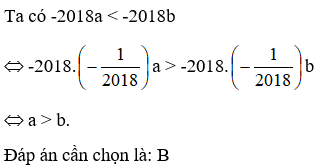Trắc nghiệm Toán 8 Bài 2: Liên hệ giữa thứ tự và phép nhân
-
256 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
21/07/2024Hãy chọn câu sai. Nếu a < b thì?
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
+ Vì a < b 2a < 2b
2a + 1 < 2b + 1 < 2b + 5
hay 2a + 1 < 2b + 5 nên A đúng.
+ Vì a < b -3a > -3b
7 - 3a > 7 - 3b > 4 - 3b
hay 7 - 3a > 4 - 3b nên B đúng.
+ Vì a < b a - b < b - b
a - b < 0 nên C đúng.
+ Vì a < b -3a > -3b
2 - 3a > 2 - 3b nên D sai.
Câu 2:
16/07/2024Cho a > b > 0. So sánh a3……b3, dấu cần điền vào chỗ chấm là?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
* Với a > b > 0 ta có:
+) a. a > a. b a2 > ab
+) Ta có: a2 > ab
a2. a > a. ab a3 > a2b
Mà a > b > 0
ab > b. b ab > b2
ab. a > b2. b a2b > b3.
a2b > b3 a3 > a2b > b3.
a3 > b3
Vậy a3 > b3.
Câu 3:
22/07/2024Cho a + 1 ≤ b + 2.
So sánh 2 số 2a + 2 và 2b + 4 nào dưới đây là đúng?
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Nhân cả hai vế của bất đẳng thức
a + 1 ≤ b + 2 với 2 > 0 ta được
2(a + 1) ≤ 2(b + 2)
2a + 2 ≤ 2b + 4.
Câu 4:
23/07/2024Cho a, b bất kì. Chọn câu đúng?
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Xét hiệu
P = - ab
= ≥ 0
(luôn đúng với mọi a, b)
Nên ≥ ab
Câu 5:
22/07/2024Với mọi a, b, c. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
P = a2 + b2 + c2 - (ab + bc + ca)
= (2a2 + 2b2 + 2c2 - 2ab - 2bc - 2ca)
= [(a2 - 2ab + b2) + (a2 - 2ac + c2) + (b2 - 2bc - c2)]
= [(a - b)2 + (a - c)2 + (b - c)2] ≥ 0
với mọi a, b, c (vì (a - b)2 ≥ 0;
(a - c)2 ≥ 0; (b - c)2 ≥ 0 với mọi a, b, c)
Nên P ≥ 0
a2 + b2 + c2 ≥ ab + bc + ac.
Câu 6:
17/07/2024Cho a, b bất kì. Chọn câu đúng nhất?
Xem đáp án
Đáp án: C
Giải thích:
Lời giải:
Xét hiệu P = a2 + b2 - 2ab
= (a - b)2 ≥ 0 (luôn đúng với mọi a, b)
Nên a2 + b2 > 2ab với mọi a, b.
Dấu “=” xảy ra khi a = b.
Câu 7:
21/07/2024Cho a - 2 ≤ b - 1.
So sánh 2 số 2a - 4 và 2b - 2 nào dưới đây là đúng?
Xem đáp án
Đáp án: D
Giải thích:
Lời giải:
Nhân cả hai vế của bất đẳng thức
a - 2 ≤ b - 1 với 2 > 0 ta được:
2(a - 2) ≤ 2(b - 1)
2a - 4 ≤ 2b - 2.
Câu 8:
16/07/2024Cho -2x + 3 < -2y + 3.
So sánh x và y. Đáp án nào sau đây là đúng?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Theo đề bài ta có: -2x + 3 < -2y + 3
-2x + 3 - 3 < -2y + 3 - 3
-2x < -2y
-2. x > -2. y
x > y.
Câu 9:
16/07/2024Cho -3x - 1 < -3y - 1.
So sánh x và y. Đáp án nào sau đây là đúng?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Theo đề bài ta có: -3x - 1 < -3y - 1
-3x - 1 + 1 < -3y - 1 + 1
-3x < -3y
-3. x > -3. y
x > y.
Câu 10:
16/07/2024Bất đẳng thức nào sau đây đúng với mọi a > 0, b > 0?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có a3 + b3 - ab2 - a2b
= a2(a - b) - b2(a - b)
= (a2 - b2) (a - b)
= (a - b)(a + b)(a - b)
= (a - b)2(a + b) ≥ 0 (vì (a - b)2 ≥ 0
với mọi a, b và a + b > 0 với a > 0, b > 0).
Câu 11:
20/07/2024Cho a > b > 0. So sánh a2 và ab; a3 và b3
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
* Với a > b > 0 ta có:
+) a. a > a. b a2 > ab
+) Ta có: a2 > ab a2.a > a. ab
a3 > a2b
Mà
a > b > 0 ab > b.b ab > b2
ab. a > b2. b a2.b > b3.
a2b > b3 a3 > a2b > b3
a3 > b3
Vậy a2 > ab và a3 > b3.
Câu 12:
21/07/2024Trong các khẳng định sau đây, khẳng định nào sai?
(1) (-4).5 < (-5).4
(2) (-7).12 ≥ (-7).11
(3) -4x2 > 0
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
+ Ta có: (-4).5 = 4.(-5) → Khẳng định (1) sai.
+ Ta có: 12 > 11 ⇒ 12.(-7) < 11.(-7) → Khẳng định (2) sai.
+ Ta có: x2 ≥ 0 ⇒ - 4x2 ≤ 0 → Khẳng định (3) sai
Câu 13:
17/07/2024Với mọi a, b, c. Khẳng định nào sau đây là đúng?
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có:
a2 + b2 + c2 - (2ab + 2bc - 2ca)
= a2 + b2 + c2 - 2ab - 2bc + 2ca
= a2 + b2 + c2 + 2a(-b) + 2c(-b) + 2ac
= [a + (-b) + c]2
= (a - b + c)2 ≥ 0, "a, b, c
Do đó a2 + b2 + c2 - (2ab + 2bc - 2ca) ≥ 0
a2 + b2 + c2 ≥ 2ab + 2bc - 2ca
Dấu “=” xảy ra khi a - b + c = 0.
Câu 16:
23/07/2024Cho x + y > 1. Chọn khẳng định đúng?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Từ x + y > 1, bình phương hai vế (hai vế đều dương) được
x2 + 2xy + y2 > 1 (1)
Từ (x - y)2 ≥ 0
suy ra x2 - 2xy + y2 ≥ 0. (2)
Cộng từng vế (1) với (2) được 2x2 + 2y2 > 1.
Chia hai vế cho 2 được x2 + y2 > .
Câu 17:
19/07/2024Cho -2020a > -2020b. Khi đó?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Ta có: -2020a > -2020b
-2020. a < -2020.b
a < b.
Câu 18:
22/07/2024Bất đẳng thức nào sau đây đúng với mọi a > 0, b > 0
Xem đáp án
Đáp án: B
Giải thích:
Lời giải:
Ta có: a3 + b3 - ab2 - a2b = a2(a - b) - b2(a - b)
= (a - b)2(a + b) ≥ 0 (vì (a - b)2 ≥ 0
với mọi a, b và a + b > 0 với a > 0, b > 0).
Do đó a3 + b3 - ab2 - a2b ≥ 0 hay a3 + b3 ≥ ab2 + a2b.
Câu 19:
16/07/2024Cho x + y ≥ 1. Chọn khẳng định đúng?
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
Từ x + y ≥ 1, bình phương hai vế (hai vế đều dương) được
x2 + 2xy + y2 ≥ 1 (1)
Từ (x - y)2 ≥ 0
suy ra x2 - 2xy + y2 ≥ 0. (2)
Cộng từng vế (1) với (2) được: 2x2 + 2y2 ≥ 1.
Chia hai vế cho 2 ta được: x2 + y2 ≥ .
Dấu “=” xảy ra khi
Câu 20:
22/07/2024Cho x > 0; y > 0. Tìm khẳng định đúng trong các khẳng định sau?
(1) (x + y) ≥ 4
(2) x2 + y3 ≤ 0
(3) (x + y) < 4
Xem đáp án
Đáp án: A
Giải thích:
Lời giải:
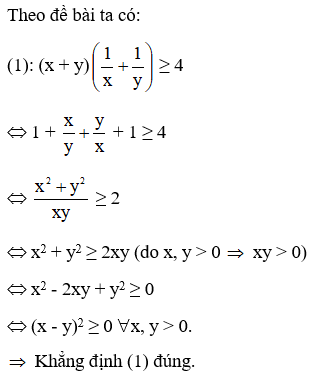
(2): x2 + y3 ≤ 0
Với
Khẳng định (2) sai.
Khẳng định (1) đúng
Khẳng định (3) sai.