Trắc nghiệm Toán 8 Bài 9: Hình chữ nhật
-
332 lượt thi
-
23 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
16/07/2024Hãy chọn câu trả lời đúng. Hình thang cân ABCD là hình chữ nhật khi:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Hình thang cân có một góc vuông là hình chữ nhật nên hình thang cân ABCD
có thêm ^BCD = 900 thì nó sẽ là hình chữ nhật nên D đúng.
Câu 2:
21/07/2024Cho tứ giác ABCD, lấy M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác ABCD cần có điều kiện gì để MNPQ là hình chữ nhật
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
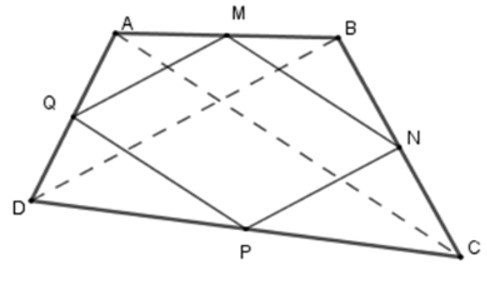
Nối AC, BD
+ Xét tam giác ABD có M, Q lần lượt là trung điểm của AB; AD
nên MQ là đường trung bình của tam giác ABD
Suy ra MQ // BD; MQ = 12BD (1)
+ Tương tự, xét tam giác CBD có N, P lần lượt là trung điểm
của BC; CD nên NP là đường trung bình của tam giác CBD.
Suy ra NP // BD; NP = 12BD (2)
Từ (1) và (2) => MQ // NP; MQ = NP
=> MNPQ là hình bình hành (dấu hiệu nhận biết)
+ Để hình bình hành MNPQ là hình chữ nhật
thì ^MQP = 900 hay MQ ⊥ QP
Lại có QP // AC (do QP là đường trung bình của tam giác DAC)
nên MQ ⊥ AC mà MQ // BD (cmt) nên AC ⊥ BD
Vậy tứ giác ABCD cần có AC ⊥ BD thì MNPQ là hình chữ nhật.
Câu 3:
16/07/2024Chọn câu đúng: Cho tứ giác ABCD có:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Ta thấy AD = BC, AD // BC, ˆA 900 thì ABCD là hình bình hành có 1 góc vuông
nên ABCD là hình chữ nhật
Câu 4:
21/07/2024Hãy chọn câu đúng. Cho ΔABC với M thuộc cạnh BC. Từ M vẽ ME song song với AB và MF song song với AC. Hãy xác định điều kiện của ΔABC để tứ giác AEMF là hình chữ nhật.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
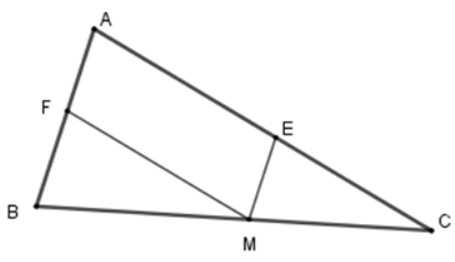
Từ giả thiết ta có ME // AF; MF // AE nên tứ giác AEMF là hình bình hành (dhnb).
Để hình bình hành AEMF là hình chữ nhật
thì = 900 nên tam giác ABC vuông tại A.
Câu 5:
21/07/2024Chọn câu sai. Tứ giác ABCD là hình chữ nhật khi
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
+ Ta thấy AB = CD = AD = BC thì ABCD chỉ có bốn cạnh bằng nhau nên ABCD chưa chắc là hình chữ nhật .
Nếu = 900 thì tứ giác ABCD có ba góc vuông nên ABCD là hình chữ nhật (do dấu hiệu tứ giác có 3 góc vuông).
+ Nếu = 900 và AB // CD thì tứ giác ABCD có
AD // BC; AB // CD nên ABCD là hình bình hành,
lại có 900 nên ABCD là hình chữ nhật. (do dấu hiệu hình bình hành có một góc vuông)
+ Nếu AB // CD; AB = CD và AC = BD thì ABCD là hình bình hành
(do có cặp cạnh đối AB; CD song song và bằng nhau),
lại có hai đường chéo bằng nhau AC = BD nên ABCD là hình chữ nhật (do dấu hiệu hình bình hành có hai đường chéo bằng nhau).
Câu 6:
23/07/2024Hãy chọn câu trả lời đúng. Hình bình hành ABCD là hình chữ nhật khi:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Vì hình bình hành có hai đường chéo bằng nhau là hình chữ nhật nên hình bình hành ABCD
có AC = BD thì ABCD là hình chữ nhật
Câu 7:
22/07/2024Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC.
1. Tứ giác ADME là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
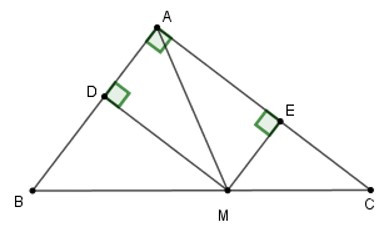
Xét tứ giác ADME có = 900 nên ADME là hình chữ nhật
Câu 8:
22/07/2024Cho tam giác ABC vuông tại A, điểm M thuộc cạnh huyền BC. Gọi D, E lần lượt là chân đường vuông góc kẻ từ M đến AB, AC.
Điểm M ở vị trí nào trên BC thì DE có độ dài nhỏ nhất?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
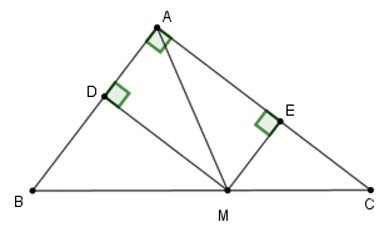
Vì ADME là hình chữ nhật (theo câu trước) nên
AM = DE (tính chất)
Để DE nhỏ nhất thì AM nhỏ nhất mà AM nhỏ nhất khi M là hình chiếu của A trên BC
Từ đó DE nhỏ nhất khi M là hình chiếu của A trên BC.
Câu 9:
23/07/2024Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 5cm, 12cm là:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
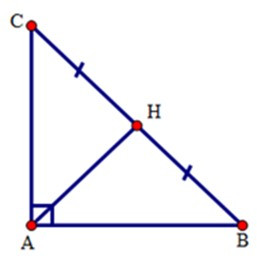
Áp dụng định lý Pytago cho tam giác ABC vuông tại A ta có:
BC2 = AC2 + AB2 hay BC2 = 52 + 122
=> BC2 = 169. Suy ra BC = 13 (cm)
Do AH là đường trung tuyến ứng với cạnh huyền BC nên
AH = BC : 2 = 13 : 2 = 6,5cm
Câu 10:
21/07/2024Hãy chọn câu sai. Hình chữ nhật có
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Từ định nghĩa là tính chất hình chữ nhật ta có A, B, D đúng và C sai.
Câu 11:
21/07/2024Cho tam giác ABC vuông tại A, AC = 6cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
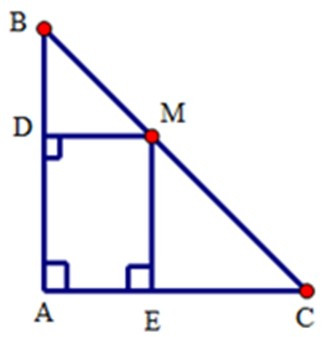
+ Xét tứ giác ADME có = 900 nên ADME là hình chữ nhật
+ Xét tam giác DMB có = 450 (do tam giác ABC vuông cân) nên tam giác BDM vuông cân tại D. Do đó Dm = BD
+ Do ADME là hình chữ nhật nên chu vi ADME là:
(AD + DM).2 = (AD + BD).2
= 6.2 = 12 cm
Vậy chu vi ADME là 12cm
Câu 12:
23/07/2024Cho tam giác ABC vuông tại A, AC = 8cm, điểm M thuộc cạnh BC. Gọi D, E theo thứ tự là các chân đường vuông góc kẻ từ M đến AB, AC. Chu vi của tứ giác ADME bằng:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
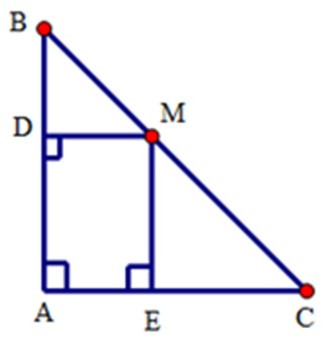
+ Xét tứ giác ADME có = 900 nên ADME là hình chữ nhật
+ Xét tam giác DMB có = 450 (do tam giác ABC vuông cân) nên tam giác BDM vuông cân tại D. Do đó DM = BD
+ Do ADME là hình chữ nhật nên chu vi ADME là:
(AD + DM).2 = (AD + BD).2 = 8.2 = 16 cm
Vậy chu vi ADME là 12cm
Câu 13:
23/07/2024Cho hình chữ nhật ABCD có AB = a;AD = b. Cho M, N, P, Q là các đỉnh của tứ giác MNPQ và lần lượt thuộc các cạnh AB, BC, CD, DA. Tìm giá trị nhỏ nhất của chu vi tứ giác MNPQ.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
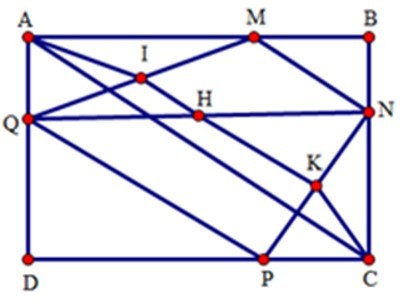
Gọi I, H, K lần lượt là trung điểm các đoạn QM, QN, PN.
Xét tam giác AQM vuông tại A có AI là đường trung tuyến nên
suy ra AI = QM
IH là đường trung bình của tam giác QMN
nên IH = MN, IH // MN
Tương tự KC = NP, HK = PQ, HK // PQ
Do đó AI + IH + HK + KC = PMNPQ
Mặt khác nếu xét các điểm A, I, H, K, C
ta có: AI + IH + HK + KC ≥ AC
Do đó PMNPQ ≥ 2AC (không đổi)
Dấu “=” xảy ra khi và chỉ khi A, I, H, K, C thẳng hang theo thứ tự đó. Điều đó tương đương với MN // AC // QP, QM // BD // NP hay MNPQ là hình bình hành
Theo định lý Pytago cho tam giác ACB vuông tại A ta có
AC2 = AB2 + BC2
= AB2 + AD2 = a2 + b2
=> AC =
Vậy giá trị nhỏ nhất của chu vi MNPQ
là 2AC = 2
Câu 14:
21/07/2024Hãy chọn câu sai. Cho ABCD là hình chữ nhật có O là giao điểm hai đường chéo. Khi đó
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
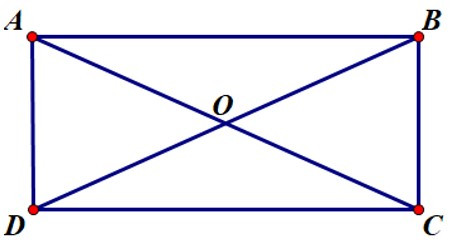
Vì ABCD là hình chữ nhật nên AB = AC; AD = BC; AC = BD
và AC, BD cắt nhau tại trung điểm O của mỗi đường.
Hay OA = OB = OC = OD nên A, B, C đúng, D sai.
Câu 15:
23/07/2024Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G. M và N lần lượt là trung điểm của GC và GB.
1. Tứ giác MNED là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
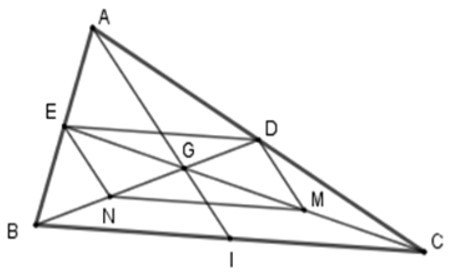
+ Xét tam giác ABC có E là trung điểm AB; D là trung điểm AC nên ED là đường trung bình của tam giác ABC
=> ED // BC; ED = BC (1)
+ Xét tam giác GBC có N là trung điểm của GB; M là trung điểm GC nên MN là đường trung bình của tam giác GBC.
=> MN // BC; MN = BC (2)
Từ (1), (2) => MN // ED, MN = ED nên tứ giác MNED là hình bình hành (dấu hiệu nhận biết)
Câu 16:
21/07/2024Cho tam giác ABC với ba trung tuyến AI, BD, CE đồng quy tại G. M và N lần lượt là trung điểm của GC và GB.
Để MNED là hình chữ nhật thì tam giác ABC cần có điều kiện:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
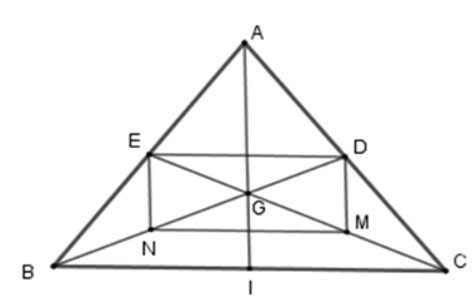
+ Xét tam giác ABG có EN là đường trung bình nên EN // AG hay EN // AI.
+ Để hình bình hành MNED là hình chữ nhật thì = 900
=> EN ⊥ MN. Mà MN // BC (câu trên) nên EN ⊥ BC
+ Lại có EN // AI suy ra AI ⊥ BC
Xét tam giác ABC có AI vừa là đường cao vừa là trung tuyến nên ΔABC cân tại A.
Câu 17:
21/07/2024Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AECH là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
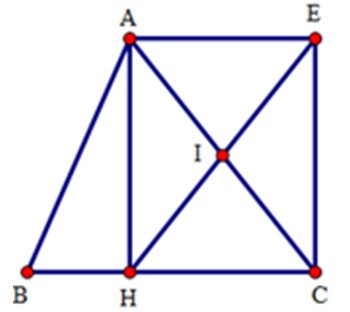
Xét tứ giác: AECH có: I là trung điểm của AC (gt); I là trung điểm của HE
(do H và E đối xứng nhau qua I)
Do đó AECH là hình bình hành (dấu hiệu nhận biết).
Lại có = 900, nên AECH là hình chữ nhật (dhnb)
Câu 18:
21/07/2024Cho hình bình hành ABCD có AB = a, BC = b (a > b). Các phân giác trong của góc A, B, C, D tạo thành tứ giác MNPQ
1. Tứ giác MNPQ là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
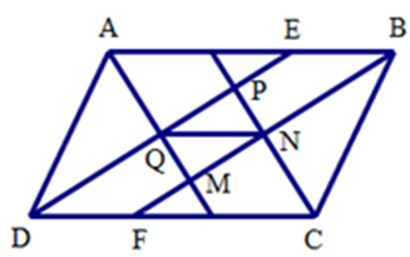

Câu 19:
23/07/2024Cho hình bình hành ABCD có AB = a, BC = b (a > b). Các phân giác trong của góc A, B, C, D tạo thành tứ giác MNPQ
2. Tính độ dài đường chéo của hình chữ nhật MNPQ theo a, b.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
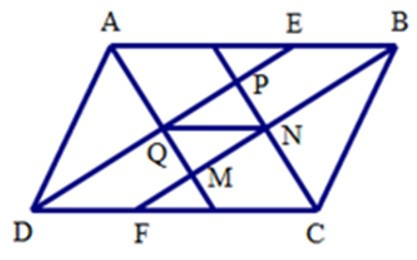
Gọi E là giao điểm PQ và AB, F là giao điểm của MN và CD.
Tam giác ADE có phân giác AQ cũng là đường cao do đó tam giác cân tại A
Suy ra DQ = QE = DE : 2
Tương tự tam giác BCF cân tại C,
do đó FN = BN = BF : 2
Ta lại có DEBF là hình bình hành (cặp cạnh đối song song),
suy ra DE = BF
Suy ra DQ = FN và DQ // FN.
Vậy DQNF là hình bình hành,
từ đó QN = DF = CD =CF
Mà CD = AB = a, CF = CB = b,
do đó: QN = a – b
Câu 20:
22/07/2024Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
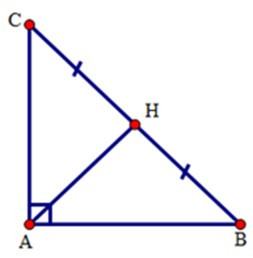
Áp dụng định lý Pytago cho tam giác ABC vuông tại A ta có:
BC2 = AC2 + AB2 hay BC2 = 62 + 82
=> BC2 = 100. Suy ra BC = 10 (cm)
Do AH là đường trung tuyến ứng với cạnh huyền BC nên
AH = BC : 2 = 10 : 2 = 5cm
Câu 21:
23/07/2024Hãy chọn câu sai.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
+ Hình thang cân có một góc vuông là hình chữ nhật nên D đúng
+ Hình bình hành có một góc vuông là hình chữ nhật nên B đúng
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật nên C đúng
+ Hình thang có một góc vuông là hình thang vuông nên A sai
Câu 22:
18/07/2024Cho hình thang cân ABCD, đáy nhỏ AB = 6, CD = 18, AD = 10.
Gọi I, K, M, L lần lượt là trung điểm của các đoạn BC, CA, AD và BD
1. Tứ giác ABKL là hình gì?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
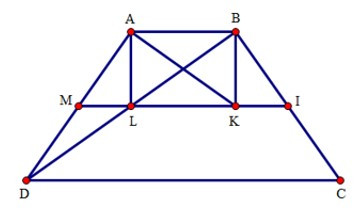
Xét tam giác ABD có: M, L lần lượt là trung điểm của AD, BD, do đó ML là đường trung bình của tam giác ABD. Suy ra ML // AB và ML = AB: 2 = 3.
Vậy ML nằm trên đường trung bình MI của hình thang ABCD. (1)
Chứng minh tương tự ta có: IK là đường trung bình của tam giác ABC.
Do đó, IK // AB và IK = AB : 2 = 3.
Vậy IK nằm trên đường trung bình MI của hình thang ABCD. (2)
Từ (1) và (2) suy ra: bồn điểm M, L, K, I nằm trên đường trung bình MI của hình thang ABCD.
Ta có: MI = (AB + CD)
= (6 + 18) = 12
(do MI là đường trung bình của hình thang ABCD)
Suy ra KL = MI – ML – KI
= 12 – 3 – 3 = 6
Xét tứ giác ABKL có:
KL = AB ( = 6); KL // AB.
Do đó ABKL là hình bình hành.
Lại có: BL = BD, AK = AC
Mà AC = BD (đường chéo hình thang cân)
Suy ra AK = BL
Xét hình bình hành ABKL có AK = KL nên suy ra ABKL là hình chữ nhật
Câu 23:
21/07/2024Cho hình thang cân ABCD, đáy nhỏ AB = 6, CD = 18, AD = 10.
Gọi I, K, M, L lần lượt là trung điểm của các đoạn BC, CA, AD và BD
Tính độ dài các cạnh AB, AL, AK.
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
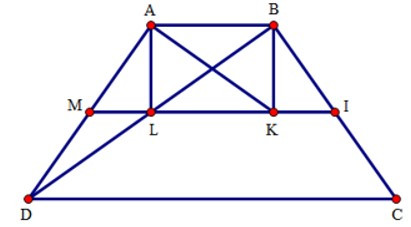
Theo câu trên ta có: AB = KL = 6
Áp dụng định lí Pitago cho tam giác vuông AML ta có:
AL2 = AM2 – ML2
= 52 – 32 = 16
Vậy AL = BK = 4
Áp dụng định lí Pitago cho tam giác vuông AKL ta có:
AK2 = AL2 + LK2
= 42 + 62 = 16 + 36 = 52
Vậy AK = BL =
Vậy AB = 6; AL = 4; AK =
Có thể bạn quan tâm
- Trắc nghiệm Hình chữ nhật (có đáp án) (331 lượt thi)
- Bài tập Hình chữ nhật (có lời giải chi tiết) (271 lượt thi)
- Trắc nghiệm Hình chữ nhật có đáp án (Nhận biết) (334 lượt thi)
- trắc nghiệm Hình chữ nhật (Thông hiểu) (271 lượt thi)
- Trắc nghiệm Hình chữ nhật có đáp án (Vận dụng) (256 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Hình bình hành (có đáp án) (865 lượt thi)
- Trắc nghiệm Tứ giác có đáp án (Nhận biết) (740 lượt thi)
- Trắc nghiệm Hình thang cân (có đáp án) (648 lượt thi)
- Trắc nghiệm Tứ giác có đáp án (Thông hiểu) (485 lượt thi)
- Trắc nghiệm Đường trung bình của tam giác, của hình thang (có đáp án) (485 lượt thi)
- Trắc nghiệm Hình thoi (có đáp án) (459 lượt thi)
- Trắc nghiệm Tứ giác (có đáp án) (456 lượt thi)
- Trắc nghiệm Tứ giác có đáp án (Vận dụng) (437 lượt thi)
- Trắc nghiệm Hình thoi có đáp án (Thông hiểu) (437 lượt thi)
- Trắc nghiệm Đường thẳng song song với một đường thẳng cho trước (có đáp án) (427 lượt thi)
