Trắc nghiệm Định lý Py - ta - go (có đáp án)
Trắc nghiệm Toán 7 Bài 7: Định lý Py - ta - go
-
614 lượt thi
-
21 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho tam giác ABC vuông ở A có AC=20cm. Kẻ AH vuông góc BC. Biết BH=9cm; HC=16cm. Tính AB, AH
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
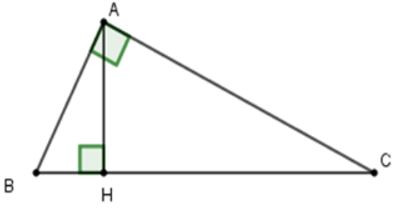
Ta có:
BC=BH+HC=9+16=25cm
Xét tam giác ABC vuông tại A, theo định lí Pytago ta có:
AB2+AC2=BC2⇒AB2+202=252⇔AB2=625-400=225⇒AB=15cm
Xét tam giác ABH vuông tại H, theo định lí Pytago ta có:
HA2+HB2=AB2⇒HA2+92=225⇒HA2=225-81=144⇒HA=12cm
Vậy AH=12cm; AB=15cm
Câu 2:
23/07/2024Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB=AC=2dm
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Vì tam giác ABC vuông cân tại tại A nên theo định lí Pytago có:
AB2+AC2=BC2 mà AB=AC=2dm
Nên
BC2=22+22=8⇒BC=√8(dm)
Câu 3:
20/07/2024Một tam giác có cạnh huyền bằng 26cm độ dài các cạnh góc vuông tỉ lệ với 5 và 12. Tính độ dài các cạnh góc vuông
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Gọi độ dài hai cạnh góc vuông là x; y (x; y>0)
Theo định lí Pytago ta có:
x2+y2=262⇔x2+y2=676
Theo bài ra ta có:
x5=y12⇒x225=y2144=x2+y225+144=676169=4
⇒x2=25.4=100⇒x=10cmy2=144.4=756⇒y=24cm
Vậy các cạnh góc vuông có độ dài 10 cm; 24 cm
Câu 4:
19/07/2024Cho tam giác ABC vuông cân ở A. Tính độ dài BC biết AB=AC=4dm
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Vì tam giác ABC vuông cân tại tại A nên theo định lí Pytago có:
AB2+AC2=BC2 mà AB=AC=4dm
Nên BC2=42+42=32⇒BC=√32(dm)
Câu 5:
23/07/2024Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
+ Với bộ số 15cm; 8cm; 18cm ta thấy
182=324; 152+82=289
Nên 289 < 324 hay 152+82<182
Nên loại A
+ Với bộ số 21dm; 20dm; 29dm ta thấy
292=841; 212+202=841
Nên 212+202=292 hay tam giác với độ dài 21dm; 20dm; 29dm thì tam giác đó là tam giác vuông (theo định lí Pytago đảo)
+Với bộ số 5m; 6m; 8m ta thấy
82=64; 52+62=41⇒82>52+62
Nên loại C
+ Với bộ số 2m; 3m; 4m ta thấy
42=16; 22+32=13⇒42>22+32
Nên loại D
Câu 6:
19/07/2024Cho tam giác MNP vuông tại P khi đó:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Vì Cho tam giác MNP vuông tại P nên theo định lí Pytago có:
MN2=NP2+MP2
Câu 7:
20/07/2024Tính cạnh huyền của một tam giác biết tỉ số các cạnh góc vuông 5:12 và chu vi tam giác bằng 60 cm
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Gọi độ dài hai cạnh góc vuông là x; y (y>x>0)(cm) và độ dài cạnh huyền là z (z>y)(cm)
Theo đề bài ta có: x5=y12 và x+y+z=60cm
Đặt x5=y12=k(k>0) suy ra x=5k; y=12k
Theo định lí Pytago ta có:
x2+y2=z2⇒z2=(5k)2+(12k)2⇒z2=169k2=(13k)2⇒z=13k
Suy ra:
x+y+z=5k+12k+13k=30k=60⇒k=2(tm)
Từ đó: z=13k=13.2=26
Vậy cạnh huyền dài 26cm
Câu 8:
18/07/2024Một tam giác có cạnh huyền bằng 20cm độ dài các cạnh góc vuông tỉ lệ với 3 và 4. Tính độ dài các cạnh góc vuông
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Gọi độ dài hai cạnh góc vuông là x; y (x; y>0)
Theo định lí Pytago ta có:
x2+y2=202⇔x2+y2=400
Theo bài ra ta có:
x3=y4⇒x29=y216=x2+y29+16=40025=16
⇒x2=16.9=144⇒x=12cmy2=16.14=256⇒y=16cm
Vậy các cạnh góc vuông có độ dài 12 cm; 16 cm
Câu 9:
22/07/2024Cho tam giác ABC vuông tại B khi đó x=1
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Vì tam giác ABC vuông tại B nên theo định lí Pytago có:
AB2+BC2=AC2
Câu 10:
19/07/2024Cho hình vẽ . Tính x
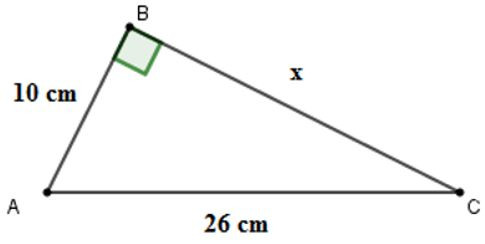
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta được:
AC2=AB2+BC2⇒BC2=AC2-AB2⇒x2=262-102=576⇒x=24cm
Vậy x = 24cm
Câu 11:
18/07/2024Cho hình vẽ . Tính x
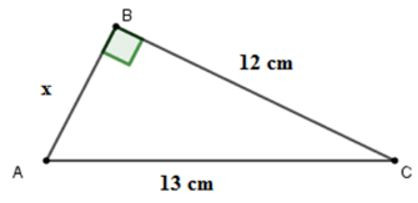
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta được:
AC2=AB2+BC2⇒AB2=AC2-BC2⇒x2=132-122=25⇒x=5cm
Vậy x = 5cm
Câu 12:
18/07/2024Tính x trong hình vẽ sau:
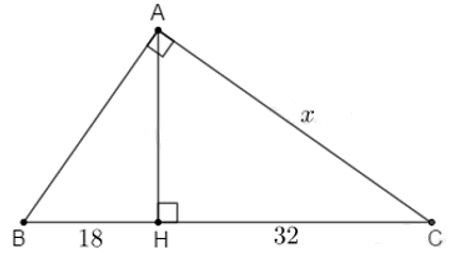
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Áp dụng định lí Pytago vào △ABH vuông tại H ta có:
AB2=AH2+BH2⇒AH2=AB2-BH2(1)
Áp dụng định lí Pytago vào △ACH vuông tại H ta có:
AC2=AH2+CH2⇒AH2=AC2-HC2(2)
Từ (1) và (2) ta có:
AB2-HB2=AC2-HC2⇒AB2-182=x2-322⇒AB2=x2-322+182⇒AB2=x2-1024+324⇒AB2=x2-700
Ta có: BC=BH+CH=18+32=50
Áp dụng định lí Pytago vào tam giác ABC vuông tại A ta có:
BC2=AB2+AC2⇒AB2+x2=502(3)
Thay AB2=x2-700 vào (3) ta được:
(x2-700)+x2=502⇒2x2=2500+700⇒2x2=3200⇒x2=3200:2=1600⇒x=√1600=40
Câu 13:
22/07/2024Cho tam giác ABC, kẻ AH vuông góc BC. Tính chu vi △ABC biết AB=5cm, AH=4cm, HC=√184cm (làm tròn đến chữ số thập phân thứ nhất)
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
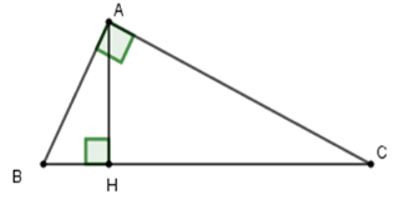
Áp dụng định lí Pytago cho tam giác ABH vuông tại H ta được:
AH2+HB2=AB2⇒HB2=AB2-AH2=52-42=9
⇒HB=3cm
Suy ra:
BC=HB+HC=3+√184cm
Áp dụng định lí Pytago cho tam giác vuông AHC ta được:
AC2=AH2+HC2=42+184=200⇒AC=√200cm
Chu vi tam giác ABC là
AB+AC+BC=5+√200+3+√184≈35,7(cm)
Câu 14:
22/07/2024Cho tam giác ABC có ˆB; ˆC là các góc nhọn. Gọi H là chân đường vuông góc hạ từ A xuống BC. Biết AH=6cm, BH=4,5cm, HC=8cm. Khi đó △ABC là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
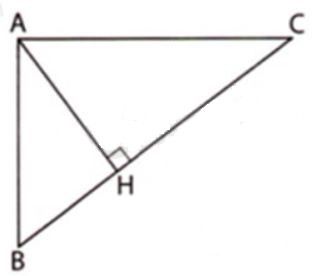
Áp dụng định lí Pytago vào △ABH vuông tại H ta có:
AB2=AH2+BH2⇒AB2=62+4,52=36+814=2254
Áp dụng định lí Pytago vào △ACH vuông tại H ta có:
AC2=AH2+CH2⇒AC2=62+82=36+64=100
Ta có: BC=BH+HC=4,5+8=252
⇒BC2=(252)2=6254(1)
Ta có:AB2+AC2=2254+100=6254(2)
Từ (1) và (2) suy ra: AB2+AC2=BC2
Vậy tam giác ABC vuông tại A
Câu 15:
21/07/2024Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
+ Với bộ số 11cm; 7cm; 8cm ta thấy
112=121; 72+82=113⇒112>72+82
Nên loại A
+ Với bộ số 12dm; 15dm; 18dm ta thấy
182=324; 122+152=369⇒122+152>182
Nên loại B
+ Với bộ số 9m; 12m; 15m ta thấy
152=225; 92+122=225⇒92+122=152
Theo định lí Pytago đảo, tam giác với ba cạnh có độ dài 9m; 12m; 15m là tam giác vuông
+Vói bộ số 6m;7m;9m ta thấy
92=81; 62+72=85⇒62+72=92
Nên loại D
Câu 16:
18/07/2024Tính x trong hình vẽ sau:
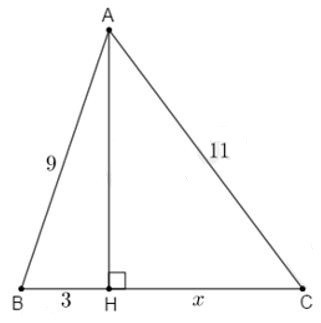
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Áp dụng định lí Pytago vào △ABH vuông tại H ta có:
AB2=AH2+BH2⇒AH2=AB2-BH2=92-32=72
Áp dụng định lí Pytago vào △ACH vuông tại H ta có:
AC2=AH2+CH2⇒HC2=AC2-AH2=112-72=49⇒x=HC=√49=7
Câu 17:
18/07/2024Cho hình vẽ. Tính x
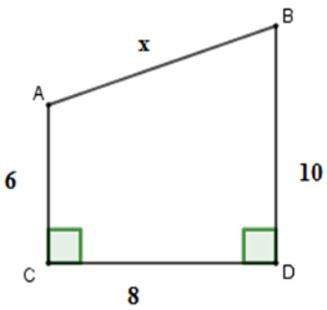
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
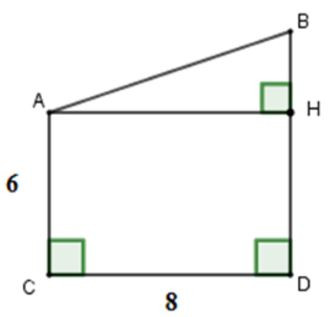
Kẻ AH⊥BD tại H
Khi đó ACDH là hình chữ nhật suy ra
HD=AC=6; AH=CD=8
Do đó: BH=BD-DH=10-6-4
Áp dụng định lí Pytago cho tam giác vuông AHB ta được:
AB2=AH2+HB2=42+82=80⇒AB=√80
Câu 18:
20/07/2024Cho tam giác ABC, kẻ AH vuông góc BC. Tính chu vi △AHB biết
AB=15cm; AH=12cm; HC=16cm
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
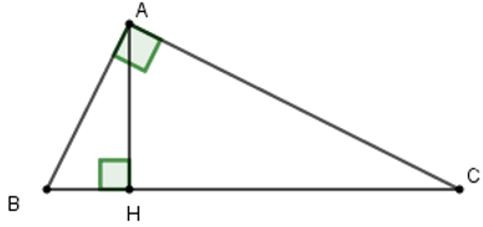
Áp dụng định lí Pytago cho tam giác ABH vuông tại H ta được:
AH2+HB2=AB2⇒HB2=AB2-AH2=152-122=81⇒HB=√81=9cm
Suy ra BC=HB+HC=9+16=25cm
Áp dụng định lí Pytago cho tam giác vuông AHC ta được:
AC2=AH2+HC2=122+62=400⇒AC=√400=20cm
Chu vi tam giác ABC là:
AB+AC+BC=15+20+25=60(cm)
Câu 19:
21/07/2024Một tam giác có độ dào ba đường cao là 4,8 cm; 6 cm; 8 cm. Tam giác đó là tam giác gì?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Gọi a,b,c lần lượt là độ dài ba cạnh của tam giác ứng với các đường cao theo thứ tự đã cho, S là diện tích △ABC (a, b, c, S>0)
Ta có: S=12.4,8A=12.6.b=12.8.c
⇒4,8a=6b=8c=2S
Do đó:
a=2S4,8=5S12b=2S6=S3c=2S8=S4
Ta có:
b2+c2=(S3)2+(S4)2=S29+S216=25S2144a2=(5S12)2=25S2144
Suy ra b2+c2=a2 nên tam giác đã cho là tam giác vuông, đỉnh góc vuông tương ứng với đường cao độ dài 4,8 cm
Câu 20:
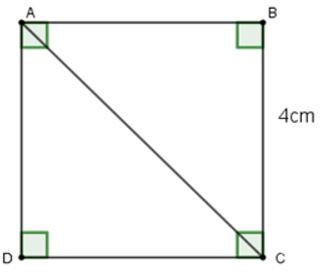
18/07/2024Cho ABCD là hình vuông cạnh 4cm (hình vẽ). Khi đó, độ dài đường chéo AC là
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Vì ABCD là hình vuông nên AB = BC = 4cm
Áp dụng định lí Pytago cho tam giác ABC vuông tại B ta có:
AC2=AB2+BC2=42+42=32⇒AC=√32(cm)
Câu 21:
20/07/2024Tính cạnh huyền của một tam giác biết tỉ số các cạnh góc vuông 3:4 và chu vi tam giác bằng 36 cm
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Gọi độ dài hai cạnh góc vuông là x; y (y>x>0)(cm) và độ dài cạnh huyền là z (z>y)(cm)
Theo đề bài ta có: x3=y4 và x+y+z=36cm
Đặt x3=y4=k(k>0) suy ra x=3k; y=4k
Theo định lí Pytago ta có:
x2+y2=z2⇒z2=(3k)2+(4k)2=25k2=(5k)2⇒z=5k
Suy ra:
x+y+z=3k+4k+5k=12k=36⇒k=3(tm)
Từ đó: x=9cm; y=12cm; z=15cm
Vậy cạnh huyền dài 15cm
Có thể bạn quan tâm
- Trắc nghiệm Định lý Py - ta - go (có đáp án) (613 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Tổng ba góc trong tam giác (có đáp án) (459 lượt thi)
- Trắc nghiệm Trường hợp bằng nhau thứ nhất của hai tam giác cạnh - cạnh - cạnh (có đáp án) (442 lượt thi)
- Trắc nghiệm Trường hợp bằng nhau thứ hai của hai tam giác cạnh - góc - cạnh (có đáp án) (433 lượt thi)
- Trắc nghiệm ôn tập chương 2 (có đáp án) (433 lượt thi)
- Trắc nghiệm Tam giác cân (có đáp án) (429 lượt thi)
- Trắc nghiệm Trường hợp bằng nhau thứ ba của hai tam giác góc - cạnh - góc (có đáp án) (384 lượt thi)
- Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông (có đáp án) (381 lượt thi)
- Trắc nghiệm Hai tam giác bằng nhau (có đáp án) (378 lượt thi)
