Trắc nghiệm Toán 7 Bài 8: Trường hợp bằng nhau của hai tam giác vuông
-
337 lượt thi
-
13 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho tam giác ABC và tam giác NPM có ; . Cần thêm một điều kiện gì để tam giác ABC và tam giác NPM bằng nhau theo trường hợp cạnh huyền - góc vuông?
Xem đáp án
Đáp án: C
Giải thích:
Ta có tam giác ABC và tam giác NPM có ; mà BC; PM là hai cạnh góc vuông của hai tam giác ABC và tam giác NPM nên để hai tam giác bằng nhau theo trường hợp cạnh huyền - góc vuông thì ta cần thêm hai cạnh huyền bằng nhau là CA = MN
Câu 2:
23/07/2024Cho tam giác DEF và tam giác JIK có: ; . Cần thêm một điều kiện gì để theo trường hợp cạnh huyền - góc vuông?
Xem đáp án
Đáp án: C
Giải thích:
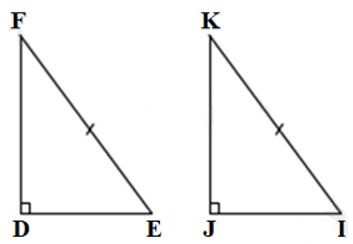
Ta có: tam giác DEF và tam giác JIK có: EF = IK; mà EF; IK là hai cạnh huyền của hai tam giác DEF và JIK nên để theo trường hợp cạnh huyền - góc vuông thì ta cần thêm hai cạnh góc vuông bằng nhau là DE = JI hoặc DF = JK.
Câu 3:
23/07/2024Cho tam giác ABC và tam giác MNP có: ; . Cần thêm một điều kiện gì để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông - góc nhọn kề?
Xem đáp án
Đáp án: A
Giải thích:
Ta có: mà góc C và góc P là hai góc nhọn kề của hai tam giác ABC và MNP
Do đó: để tam giác ABC và tam giác MNP theo trường hợp cạnh góc vuông - góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn và của hai tam giác này bằng nhau, tức là bổ sung thêm điều kiện AC = MP.
Câu 4:
23/07/2024Cho tam giác PQR và tam giác TUV có ; . Cần thêm một điều kiện gì để tam giác PQR và tam giác TUV theo trường hợp cạnh góc vuông - góc nhọn kề:
Xem đáp án
Đáp án: B
Giải thích:
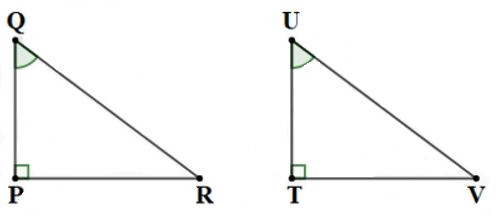
Ta có: mà góc Q và góc U là hai góc nhọn kề của hai tam giác PQR và tam giác TUV
Do đó: để tam giác PQR và tam giác TUV theo trường hợp cạnh góc vuông - góc nhọn kề thì cần cặp cạnh góc vuông kề với hai góc nhọn và của hai tam giác này bằng nhau, tức là bổ sung thêm điều kiện PQ = TU.
Câu 5:
23/07/2024Cho tam giác ABC và tam giác DEF có: ; AC = DF;
Phát biểu nào trong các phát biểu sai đây là đúng
Xem đáp án
Đáp án: A
Giải thích:
Xét tam giác ABC và tam giác FED có:
(gt)
AC = DF (gt)
(gt)
(cạnh huyền - góc nhọn)
Câu 6:
23/07/2024Cho tam giác ABC và tam giác DEF có AB = DE; ; . Biết AC = 9cm. Độ dài DF là:
Xem đáp án
Đáp án: C
Giải thích:
Xét tam giác ABC và tam giác DEF có:
AB = DE;
(cạnh góc vuông - góc nhọn)
Suy ra DE = AC = 9cm (hai cạnh tương ứng)
Câu 7:
18/07/2024Cho tam giác ABC và tam giác DEF có , , . Biết , . Độ dài EF là:
Xem đáp án
Đáp án: C
Giải thích:
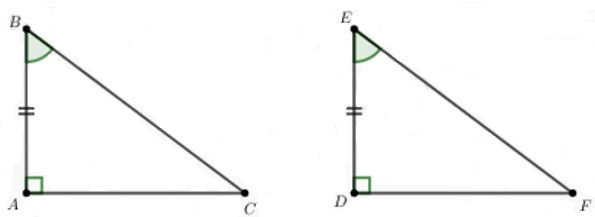
Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:
Xét tam giác ABC và tam giác DEF có:
(cạnh góc vuông - góc nhọn kề)
(hai cạnh tương ứng)
Câu 8:
23/07/2024Cho tam giác DEF và tam giác HKI có , , . Biết . Số đo góc I là:
Xem đáp án
Đáp án: C
Giải thích:
Xét tam giác DEF và tam giác HKI có
(cạnh góc vuông - góc nhọn)
(hai góc tương ứng)
Câu 9:
23/07/2024Cho hình vẽ. Chọn câu đúng
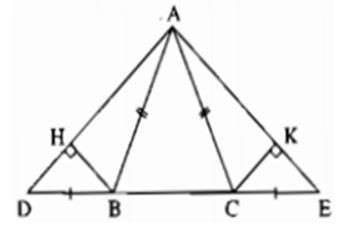
Xem đáp án
Đáp án: D
Giải thích:
Vì tam giác ABC cân tại A (do AB = AC) nên (tính chất)(1)
Lại có: và (hai góc kề bù)
Suy ra:
(2)
Từ (1) và (2) suy ra
Xét tam giác ABD và tam giác ACE có:
AB = AC
BD = CE
(hai góc tương ứng)
Xét tam giác AHB và AKC có:
AB = AC
Câu 10:
23/07/2024Cho tam giác ABC có M là trung điểm của BC và AM là tia phân giác của góc A. Khi đó, tam giác ABC là tam giác gì?
Xem đáp án
Đáp án: D
Giải thích:
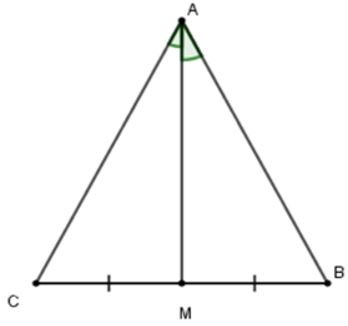
Tam giác ABC có AM vừa là đường trung tuyến vừa là đường phân giác nên cân tại A
Câu 11:
23/07/2024Cho tam giác ABC cân tại A có: tại H. Tính số đo góc BAH biết
Xem đáp án
Đáp án: B
Giải thích:
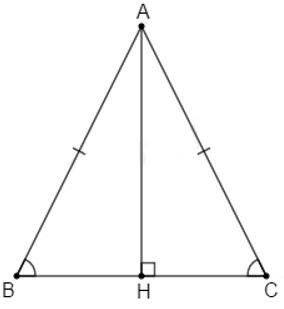
cân tại A, suy ra
Xét hai tam giác vuông AHB và AHC có:
(hai góc tương ứng)
Mặt khác suy ra:
Câu 12:
19/07/2024Cho tam giác ABC vuông cân tại A. Một đường thẳng d bất kì luôn đi qua A. Kẻ BH và CK vuông goc với đường thẳng d. Khi đó bằng:
Xem đáp án
Đáp án: C
Giải thích:
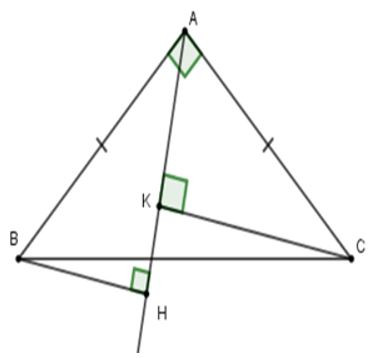
Vì vuông cân tại A nên (tính chất)
Lại có: (vì vuông tại H) và
Nên (cùng phụ với )
(cạnh huyền - góc nhọn) suy ra
Do đó (1)
Xét tam giác ACK, theo định lí Pytago:
(2)
Từ (1)và (2) suy ra
Câu 13:
23/07/2024Cho tam giác ABC vuông cân tại A, có AC = 8cm. Một đường thẳng d bất kì luôn đi qua A. Kẻ BH và CK vuông góc với đường thẳng d. Khi đó bằng:
Xem đáp án
Đáp án: C
Giải thích:
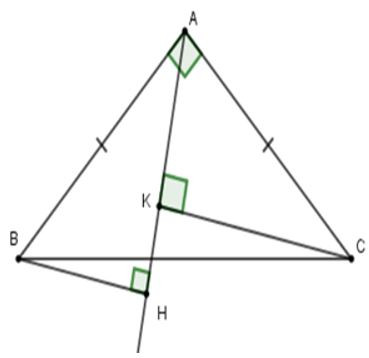
Vì vuông cân tại A nên (tính chất)
Lại có: (vì vuông tại H) và
Nên (cùng phụ với )
(cạnh huyền - góc nhọn) suy ra
Do đó (1)
Xét tam giác ACK, theo định lí Pytago:
(2)
Từ (1)và (2) suy ra