Trắc nghiệm Trường hợp bằng nhau thứ ba của hai tam giác góc - cạnh - góc (có đáp án)
Trắc nghiệm Toán 7 Bài 5: Trường hợp bằng nhau thứ ba của hai tam giác góc - cạnh - góc
-
370 lượt thi
-
17 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Cho tam giác PQR và tam giác DEF có: , , . Phát biểu nào trong các phát biểu sau đây đúng:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
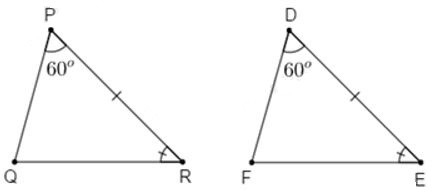
Xét tam giác PQR và tam giác DEF có
Câu 2:
23/07/2024Cho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ đường thẳng song song với Oy cắt Oz ở M. Qua M kẻ đường thẳng song song với Ox cắt Oy ở B. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
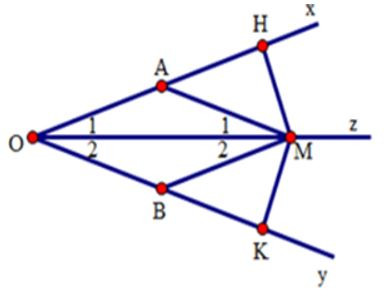
Ta có:
(hai góc so le trong)
(hai góc so le trong)
(do Oz là tia phân giác của góc xOy)
Do đó
Xét tam giác AOM và tam giác BOM có:
(cmt)
OM cạnh chung
(cmt)
Do đó: (các cặp cạnh tương ứng)
Câu 3:
22/07/2024Cho hai đoạn thẳng AB, CD song song với nhau. Hai đoạn thẳng này chắn giữa hai đường thẳng song song AC, BD. Chọn câu đúng:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
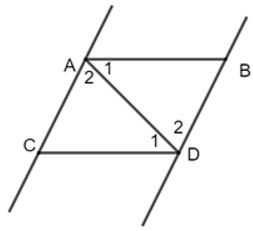
Kẻ đoạn thẳng AD
Vì AB//CD (gt) nên (hai góc so le trong)
Vì AC//BD (gt) nên (hai góc so le trong)
Xét tam giác ABD và tam giác DCA có:
(cmt)
AD là cạnh chung
(cmt)
(hai cạnh tương ứng)
Câu 4:
23/07/2024Cho tam giác ABC có AB = AC. Trên cạnh AB và AC lấy các điểm D, E sao cho AD = AE. Gọi K là giao điểm BE và DC. Chọn câu sai:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
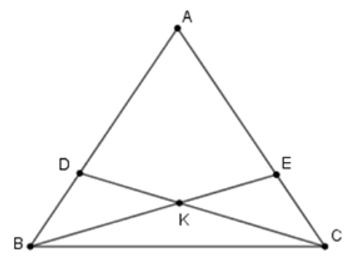
Xét tam giác ABE và tam giác ACD có:
(hai góc tương ứng)
(hai cạnh tương ứng)
A đúng
Lại có:
(hai góc kề bù)
Mà (cmt)
Suy ra
Lại có: AB = AC; AD = AE (gt)
C đúng
Xét tam giác KBD và tam giác KCE có:
(hai cạnh tương ứng)
B đúng, D sai
Câu 5:
20/07/2024Cho tam giác DEF và tam giác HKG có , , . Biết . Số đo góc H là:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
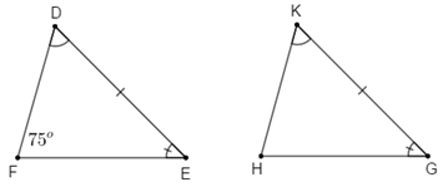
Xét tam giác DEF và tam giác HKG có
(hai góc tương ứng)
Câu 6:
18/07/2024Cho tam giác ABC và tam giác DEF có , , . Biết . Độ dài DF là:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Xét tam giác ABC và tam giác DEF có:
AB = DE
(hai cạnh tương ứng)
Câu 7:
22/07/2024Cho tam giác MNP và tam giác DEF có ; ; . Biết . Độ dài NP là:
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
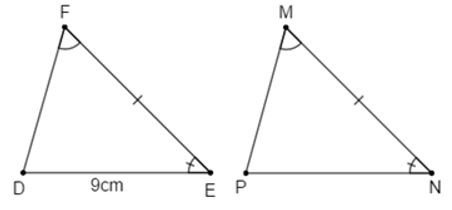
Xét tam giác MNP và tam giác DEF có
MN = EF
(hai cạnh tương ứng)
Câu 8:
22/07/2024Cho tam giác ABC vuông tại A có . Qua A kẻ đường thẳng xy sao cho B, C nằm cùng phía với xy. Kẻ BD và CE vuông góc với xy. Chọn câu đúng:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
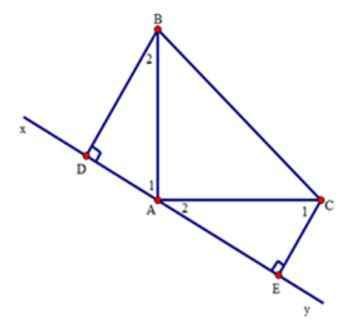
Ta có: (do )
Mà vì tam giác ABD vuông tại D
(cùng phụ với )
Lại có: vì tam giác ACE vuông tại E
(cùng phụ với )
Xét tam giác BDA và tam giác AEC có:
(cạnh huyền-góc nhọn)
( hai cạnh tương ứng)
Do đó:
Câu 9:
22/07/2024Cho tam giác ABC vuông tại A có . Qua A kẻ đường thẳng xy sao cho B, C nằm cùng phía với xy. Kẻ BD và CE vuông góc với xy. Tính DE biết
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
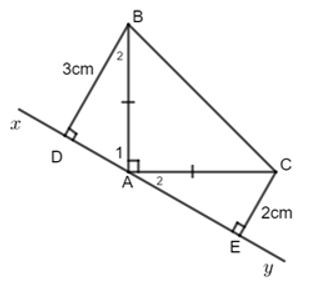
Ta có: (do )
Mà vì tam giác ABD vuông tại D
(cùng phụ với )
Xét tam giác BDA và tam giác AEC có:
(cạnh huyền-góc nhọn)
( hai cạnh tương ứng)
Do đó:
Câu 10:
22/07/2024Cho tam giác ABC có . Tia phân giác của góc A cắt BC ở K. Từ B kẻ đường thẳng vuông góc với AK cắt H tại AC ở D. Chọn câu sai
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
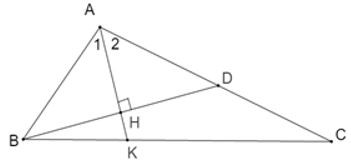
Vì AK là tia phân giác của nên
Theo giả thiết ta có:
Xét tam giác AHB và tam giác AHD có:
(cmt)
AH là cạnh chung
(hai cạnh tương ứng)
(hai góc tương ứng)
Câu 11:
23/07/2024Cho tam giác ABC và MNP có , , . Phát biểu nào trong các phát biểu sau đây đúng:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Xét tam giác ABC và tam giác MNP có:
(cạnh huyền- góc nhọn)
Câu 12:
22/07/2024Cho tam giác ABC, D là trung điểm của AB. Đường thẳng qua D và song song với BC cắt AC ở E, đường thẳng qua E và song song với AB cắt BC ở F. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
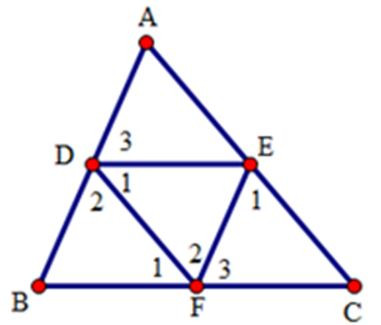
Xét tam giác DEF và tam giác FBD có:
(hai góc so le trong)
DF là cạnh chung
(hai góc so le trong)
(hai cạnh tương ứng)
Mà AD = BD nên EF = AD
Ta có: (hai góc đồng vị); (hai góc đồng vị)
Xét tam giác ADE và tam giác EFC có:
(cmt)
(hai góc đồng vị)
AD = EF (cmt)
Tương tự chứng minh được
Từ (1) và (2) suy ra (3)
Câu 13:
22/07/2024Cho tam giác ABC và tam giác NPM có ; . Cần thêm một điều kiện gì để tam giác MPN và tam giác CBA bằng nhau theo trường hợp góc - cạnh- góc?
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Áp dụng trường hợp bằng nhau thứ ba của tam giác ta thấy cần thêm một điều kiện về góc kề cạnh đó
Câu 14:
22/07/2024Cho tam giác ABC có . Tia phân giác của góc B cắt AC ở D, tia phân giác của góc C cắt AB ở E. Các tia phân giác đó cắt nhau ở I. Tính độ dài ID, biết IE = 2cm.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
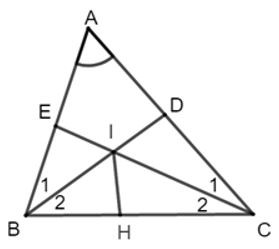
Vì BD là tia phân giác của nên
Vì CE là tia phân giác của nên
Xét có
(tổng ba góc trong tam giác bằng )
Mà nên
Ta lại có:
Xét có:
(tổng ba góc trong tam giác bằng )
Mà nên
Mặt khác (hai góc kề bù)
Khi đó (hai góc đối đỉnh)(1)
Kẻ tia phân giác của cắt BC tại H
Suy ra (2)
Từ (1) và (2) suy ra
Xét tam giác CID và tam giác CIH có:
(cmt)
CI là cạnh chung
(cmt)
(hai cạnh tương ứng)(4)
Từ (3) và (4) suy ra ID = IE = 2cm
Câu 15:
22/07/2024Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax; By vuông góc với AB. Gọi C là một điểm thuộc D. Khi đó:
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
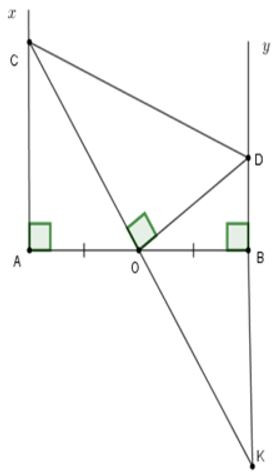
Kéo dài OC cắt BD tại K. Khi đó:
Xét tam giác AOC và tam giác BOK có:
OA = OB (O là trung điểm của AB)
(hai góc đối đỉnh)
(hai cạnh tương ứng)
Xét tam giác DOC và tam giác DOK có:
OC = OK (cmt)
Cạnh OD chung
(hai cạnh tương ứng)
Ta có: DK = DB + BK mà (cmt) nên
Câu 16:
22/07/2024Cho đoạn thẳng AB, O là trung điểm AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax; By vuông góc với AB. Gọi C là một điểm thuộc D. Tính DC biết AC = 5cm; BD = 2cm
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
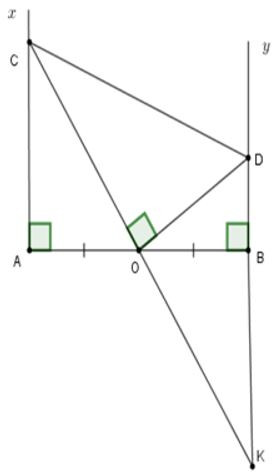
Kéo dài OC cắt BD tại K. Khi đó:
Xét tam giác AOC và tam giác BOK có:
OA = OB (O là trung điểm của AB)
(hai góc đối đỉnh)
(hai cạnh tương ứng)
Xét tam giác DOC và tam giác DOK có:
OC = OK (cmt)
Cạnh OD chung
(hai cạnh tương ứng)
Ta có: DK = DB + BK mà (cmt)
Vậy CD = 7cm
Câu 17:
20/07/2024Cho tam giác ABC và MNP có , . Cần thêm một điều kiện gì để tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc - cạnh- góc?
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Ta thấy hai tam giác ABC và MNP có hai yếu tố về góc ,
Để tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc - cạnh- góc thì cần thêm điều kiện về cạnh kề hai góc đã cho đó là AB = MN
Có thể bạn quan tâm
- Trắc nghiệm Trường hợp bằng nhau thứ ba của hai tam giác góc - cạnh - góc (có đáp án) (369 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Định lý Py - ta - go (có đáp án) (588 lượt thi)
- Trắc nghiệm Tổng ba góc trong tam giác (có đáp án) (437 lượt thi)
- Trắc nghiệm Trường hợp bằng nhau thứ nhất của hai tam giác cạnh - cạnh - cạnh (có đáp án) (429 lượt thi)
- Trắc nghiệm Trường hợp bằng nhau thứ hai của hai tam giác cạnh - góc - cạnh (có đáp án) (416 lượt thi)
- Trắc nghiệm Tam giác cân (có đáp án) (410 lượt thi)
- Trắc nghiệm ôn tập chương 2 (có đáp án) (409 lượt thi)
- Trắc nghiệm Trường hợp bằng nhau của hai tam giác vuông (có đáp án) (364 lượt thi)
- Trắc nghiệm Hai tam giác bằng nhau (có đáp án) (345 lượt thi)
