Trắc nghiệm Diện tích đa giác (có đáp án)
Trắc nghiệm Toán 8 Bài 6: Diện tích đa giác
-
284 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Cho hình vuông ABCD có cạnh 10m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng diện tích vuông ABCD.
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
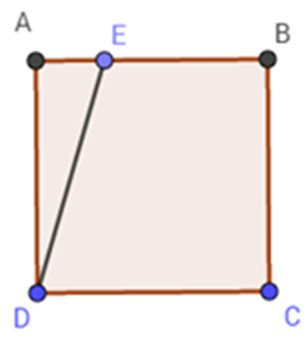
Gọi BE = x (m).
Diện tích hình vuông ABCD là:
SABCD = AB2 = 102 = 100 (m2)
Diện tích hình than vuông BCDE là:
SBCDE =
= = 5 (x+10)
Vì diện tích hình thang vuông BCDE bằng diện tích hình vuông ABCD nên ta có: SBCDE = SABCD
= 5(x + 10) = .100
x + 10 = 16
x = 6 (m)
Câu 2:
17/07/2024Cho hình vuông ABCD có cạnh 20 m. Hãy xác định điểm E trên cạnh AB sao cho diện tích hình thang vuông BCDE bằng diện tích vuông ABCD.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
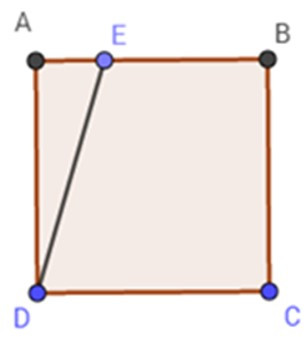
Gọi BE = x (m).
Diện tích hình vuông ABCD là:
SABCD = AB2 = 202 = 400 (m2)
Diện tích hình than vuông BCDE là:
SBCDE =
= = 10(x + 20)
Vì diện tích hình thang vuông BCDE bằng diện tích hình vuông ABCD nên ta có:
SBCDE = SABCD = 10(x + 20) = .400
x + 20 = 30 x = 10 (m)
Vậy điểm E ở trên cạnh AB sao cho BE = 10 m hay E là trung điểm đoạn AB.
Câu 3:
23/07/2024Cho hình bình hành ABCD có = 1200, AB = 2BC. Gọi I là trung điểm CD, K là trung điểm của AB. Biết chu vi hình bình hành ABCD bằng 60cm. Tính diện tích hình bình hành ABCD.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
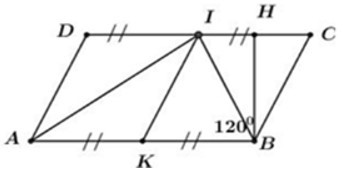
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD
=> SABCD = BH.CD
Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.

=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 600).
=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.
=> HI = HC = BC = 5cm
Áp dụng định lý Pytago với tam giác vuông HBC ta có:
=> SABCD = BH.AB
= BH.2BC = .2.10
= 100 cm2
Câu 4:
19/07/2024Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC.
Vẽ BP ⊥ MN; CQ ⊥ MN (P, Q Є MN). So sánh SBPQC và SABC.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
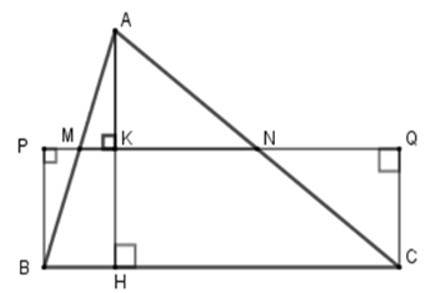
Kẻ AH ⊥ BC tại H và AH cắt MN tại K.
+ Xét tam giác ABC có MN là đường trung bình nên MN // BC suy ra AH ⊥ MN tại K. Xét tứ giác CBPQ
có PQ // BC (do MN // BC) và PB // CQ (do cùng vuông góc với PQ) nên CBPQ là hình bình hành.
Lại có = 900 nên tứ giác CBPQ là hình chữ nhật.
Suy ra SCBPQ = BP. BC.
+ Xét ΔBPM và ΔAKM có:
Suy ra ΔBPM = ΔAKM (ch – gn)
=> BP = AK (hai cạnh tương ứng) (1)
Xét ΔABK có MK // BH (do MN//BC) và M là trung điểm của AB nên K là trung điểm của AH (định lý về đường trung bình của tam giác).
Nên AK = AH (2)
Từ (1) và (2) ta có PB = AH.
+ SABC = AH. BC
mà PB = AH (cmt)
nên SABC = PB. BC
Lại có SCBPQ = BP. BC (cmt)
nên ta có SABC = SCBPQ
Câu 5:
15/07/2024Tam giác ABC có hai trung tuyến AM và BN vuông góc với nhau. Hãy tính diện tích tam giác đó theo hai cạnh AM và BN.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
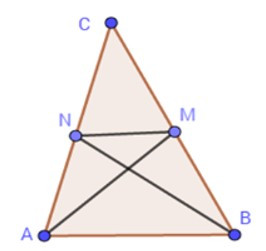
Ta có ABMN là tứ giác có hai đường chéo AM và BN vuông góc nên có diện tích là:
SABMN = AB.MN
Hai tam giác AMC và ABC có chung đường cao hạ từ A nên
=> SAMC = SABC (1)
Hai tam giác AMN và AMC có chung đường cao hạ từ M nên
=> SAMB = SABC (2)
Từ (1) và (2) suy ra SAMN = SABC
Hai tam giác AMB và ABC có chung đường cao hạ từ A nên
=> SAMB = SABC
Ta có: SABMN = SAMN + SABM
= SABC + SABC = SABC
=> SABC = SABMN
=.AM.BN = AM.BN
Câu 6:
15/07/2024Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Vẽ BP ⊥ MN; CQ ⊥ MN (P, Q Є MN). Biết SABC = 50 cm2, tính SBPQC.
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
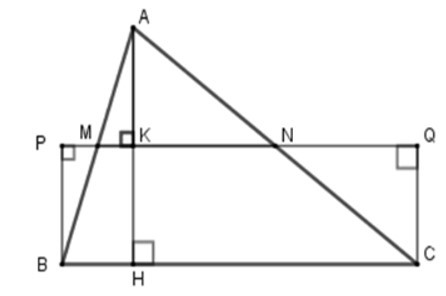
Kẻ AH ⊥ BC tại H và AH cắt MN tại K.
+ Xét tam giác ABC có MN là đường trung bình nên MN // BC suy ra AH ⊥ MN tại K.
Xét tứ giác CBPQ có PQ // BC (do MN // BC) và PB // CQ (do cùng vuông góc với PQ) nên CBPQ là hình bình hành.
Lại có = 900 nên tứ giác CBPQ là hình chữ nhật.
Suy ra SCBPQ = BP. BC.
+ Xét ΔBPM và ΔAKM có:
Suy ra ΔBPM = ΔAKM (ch – gn)
=> BP = AK (hai cạnh tương ứng) (1)
Xét ΔABK có MK // BH (do MN//BC) và M là trung điểm của AB nên K là trung điểm của AH (định lý về đường trung bình của tam giác).
Nên AK = AH (2)
Từ (1) và (2) ta có PB = AH.
+ SABC = AH. BC mà
PB = AH (cmt)
nên SABC = PB. BC
Lại có SCBPQ = BP. BC (cmt) nên
ta có SABC = SCBPQ = 50 cm2.
Câu 7:
23/07/2024Cho tam giác vuông tại ABC. Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Biết SBCHI = 100 cm2, tính SACFG + SABDE
 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
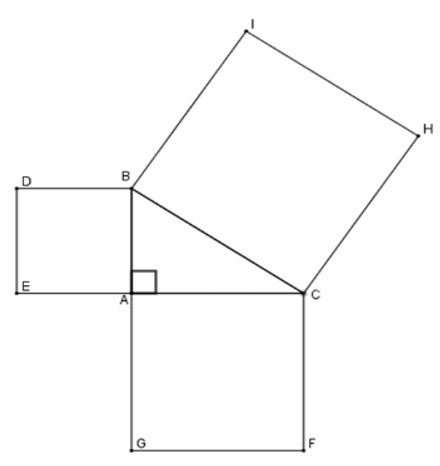
Ta có: SBCHI = BC2; SACFG = AC2; SABDE = AB2
Theo định lý Pytago cho tam giác ABC vuông tại A
ta có: BC2 = AB2 + AC2
=> SBCHI = SACFG + SABDE
Vậy SACFG + SABDE = SBCHI = 100 cm2
Câu 8:
21/07/2024Cho tam giác vuông tại ABC.
Về phía ngoài tam giác, vẽ các hình vuông ABDE, ACFG, BCHI. Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
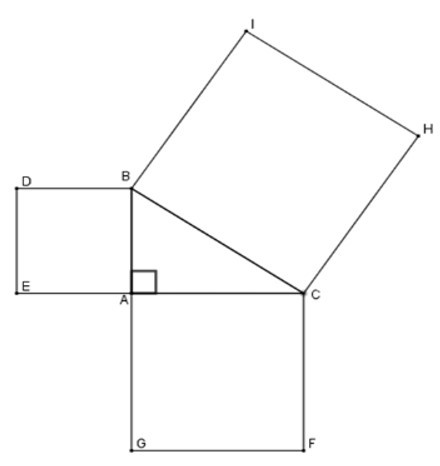
Ta có: SBCHI = BC2;
SACFG = AC2; SABDE = AB2
Theo định lý Pytago cho tam giác ABC vuông tại A
ta có: BC2 = AB2 + AC2
=> SBCHI = SACFG + SABDE
Câu 9:
22/07/2024Trong các hình thoi có chu vi bằng nahu, hình nào có diện tích lớn nhất?
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
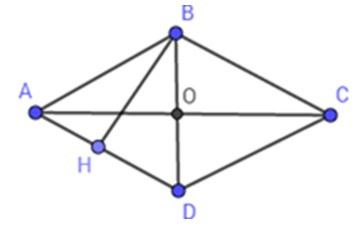
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau.
Kẻ BH vuông góc với AD. Ta có SABCD = AD. BH
Trong tam giác vuông ABH vuông tại H thì:
BH ≤ AB (đường vuông góc ngắn hơn đường xiên)
Do đó: SABCD = AD. BH ≤ AD. AB
= AB. AB = AB2
SABCD có giá tị lớn nhất bằng AB2 khi ABCD là hình vuông.
Vây trong các hình thoi có cùng chu vi thì hình vuông có diện tích lớn nhất.
Câu 10:
15/07/2024Cho hình thoi ABCD có BD = 60 cm, AC = 80 cm.
Vẽ các đường cao BE VÀ BF. Tính diện tích tứ giác BEDF.
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
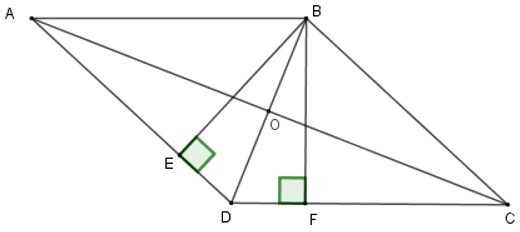
Gọi O là giao điểm của AC, BD.
Vì ABCD là hình thoi nên AC ⊥ BD;
OA = OC = = 40 cm;
OB = OD = = 30 cm.
Xét tam giác vuông AOB, theo định lý Pytago ta có:
AB2 = OA2 + OB2
= 402 + 302 = 2500
=> 50 CM
Lại có:
SABCD = = 2400 cm2
mà SABCD = BE. AD
BE.50 = 2400
BE = 48 cm (vì AD = AB = 50 cm)
Xét tam giác vuông BED có:
ED2 = BD2 – BE2
= 602 – 482 = 1296
=> ED = 36
Suy ra: SBED = DE. BE
= 48.36 = 864 cm2.
Lại có: ΔBED = ΔBFD (ch – gn)
nên SBFD = SBED = 864 cm2.
Từ đó: SBEDF = SBFD + SBED
= 864 + 864 = 1728 cm2
Câu 11:
22/07/2024Cho hình vuông MNPQ nội tiếp tam giác ABC vuông cân tại A (hình vẽ). Biết SMNPQ = 484cm2. Tính SABC.
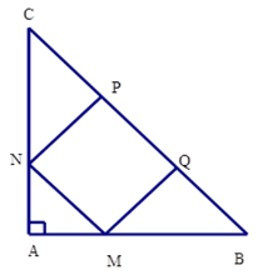
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
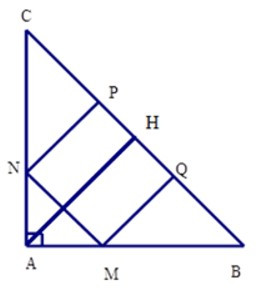
Ta có
Kẻ AH ⊥ BC => H là trung điểm cạnh BC (vì tam giác ABC vuông cân tại A)
Khi đó AH là đường trung tuyến nên
AH = (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)
+ Xét tam giác vuông CNP
có = 450 (do tam giác ABC vuông cân) nên tam giác CNP vuông cân tại P
Suy ra CP =PN = 22cm
+ Tương tự ta có ΔQMB vuông cân tại Q
=> QM = QB = 22cm
Từ đó BC = PC + PQ + QB
= 22 + 22 + 22 = 66cm
Mà AH = (cmt)
=> AH = = 33cm
Từ đó SABC = AH.BC
= .33.66 = 1089 cm2
Câu 12:
15/07/2024Cho tam giác ABC có diện tích 12cm2. Gọi N là trung điểm của BC, M trên AC
sao cho AM = AC, AN cắt BM tại O.
1. Chọn câu đúng
 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
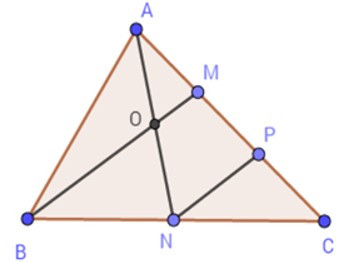
Lấy P là trung điểm của CM.
Vì AM = AC => MC = AC
=> MP = PC = AC = AM
Tam giác BCM có:
Suy ra NP là đường trung bình của tam giác BMC (định nghĩa).
Suy ra NP // BM (tính chất đường trung bình).
Tam giác ANP có:
=> AO = ON (định lý đảo của đường trung bình).
Theo chứng minh trên ta có OM là đường trung bình của tam giác ANP
nên OM = NP (1)
NP là đường trung bình của tam giác BCM
nên NP = BM (2)
Từ (1) và (2) suy ra BM = 4OM
=> BO = 3OM
Vậy cả A, B đều đúng
Có thể bạn quan tâm
- Trắc nghiệm Diện tích đa giác (có đáp án) (283 lượt thi)
- Bài tập Diện tích đa giác (có lời giải chi tiết) (231 lượt thi)
- Trắc nghiệm Diện tích đa giác có đap án (Vận dụng) (226 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Diện tích tam giác (có đáp án) (417 lượt thi)
- Trắc nghiệm Ôn tập Chương 2 Hình học: Đa giác. Diện tích đa giác (có đáp án) (398 lượt thi)
- Trắc nghiệm Đa giác. Đa giác đều có đáp án (Thông hiểu) (366 lượt thi)
- Trắc nghiệm Diện tích tam giác có đáp án (Vận dụng) (345 lượt thi)
- Trắc nghiệm Toán 8 Bài 1(có đáp án): Đa giác. Đa giác đều ( Phần 1) (331 lượt thi)
- Trắc nghiệm Ôn tập chương 2 có đáp án (Vận dụng) (324 lượt thi)
- Trắc nghiệm Đa giác. Đa giác đều có đáp án (Nhận biết) (324 lượt thi)
- Trắc nghiệm Diện tích hình thoi (có đáp án) (323 lượt thi)
- Trắc nghiệm Đa giác. Đa giác đều (có đáp án) (317 lượt thi)
- Trắc nghiệm Diện tích hình thang (có đáp án) (308 lượt thi)
