Trắc nghiệm Toán 8 Bài Ôn tập chương 2 Hình học
-
370 lượt thi
-
20 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
20/07/2024Hãy chọn câu đúng:
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
+) Diện tích hình chữ nhật bằng tích hai kích thước của nó
+) Diện tích hình vuông có cạnh a là a2
+) Diện tích tam giác vuông bằng nửa tích hai cạnh góc vuông của tam giác vuông đó.
Câu 2:
17/07/2024Đa giác đều là đa giác
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Theo định nghĩa: Đa giác đều là đa giác có tất cả các cạnh bằng nhau và các góc bằng nhau.
Câu 3:
16/07/2024Hình chữ nhật có chiều dài tang 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
Theo công thức tính diện tích hình chữ nhật S = a.b thì diện tích hình chữ nhật tỉ lệ thuận với chiều dài và chiều rộng của nó
Nếu a’ = 4a; b’ = b
thì S’ = a’.b’ = 4a. b = 2S
Do đó diện tích mới bằng 2 lần diện tích đã cho
Câu 4:
16/07/2024Số đo mỗi góc của hình 9 cạnh đều là
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Số đo góc của đa giác đều 9 cạnh: =
Câu 5:
21/07/2024Một đa giác lồi 10 cạnh thì có số đường chéo là:
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Số đường chéo của hình 10 cạnh là: đường
Câu 6:
18/07/2024Tổng số đo các góc của hình đa giác n cạnh là 9000 thì
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
Áp dụng công thức tính tổng số đo các góc trông đa giác n cạnh là:
(n – 2).1800 (với n ≥ 3), ta có:
(n – 2).1800 = 9000
=> (n – 2) = 9000 : 1800
=> n – 2 = 5 => n = 7
Câu 7:
20/07/2024Hình chữ nhật có diện tích là 240cm2, chiều rộng là 8cm. Chu vi hình chữ nhật đó là:
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Chiều dài hình chữ nhật là: 240 : 8 = 30cm
Chu vi hình chữ nhật là: 2.(30 + 8) = 76(cm)
Câu 8:
21/07/2024Hình chữ nhật có diện tích là 240cm2, chiều rộng là 8cm. Chu vi hình chữ nhật đó là:
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Chiều dài hình chữ nhật là: 240 : 8 = 30cm
Chu vi hình chữ nhật là: 2.(30 + 8) = 76(cm)
Câu 9:
23/07/2024Một tam giác có độ dài ba cạnh là 12cm, 5cm, 13cm. Diện tích tam giác đó là
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
Ta có: 52 + 122 = 169; 132 = 169
=> 52 + 122 = 132
Do đó đây tam giác đã cho là tam giác vuông có hai cạnh góc vuông là 5cm và 12cm.
Diện tích của nó là: (cm2)
Câu 10:
18/07/2024Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Chọn câu đúng.
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
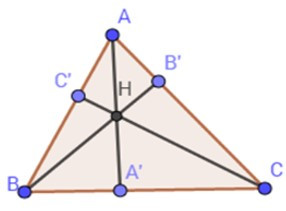
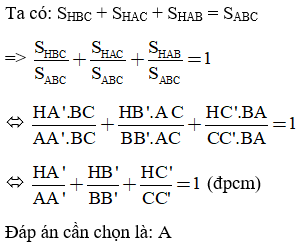
Câu 11:
22/07/2024Cho tam giác ABC trung tuyến AM, chiều cao AH. Chọn câu đúng
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
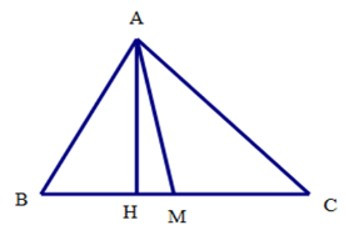
Câu 12:
22/07/2024Cho hình chữ nhật ABCD có AD = 8cm, AB = 9cm.
Các điểm M, N trên đường chéo BD sao cho BM = MN = ND. Tính diện tích tam giác CMN.
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
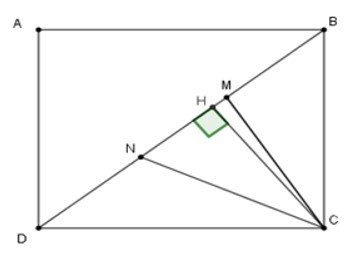
Câu 13:
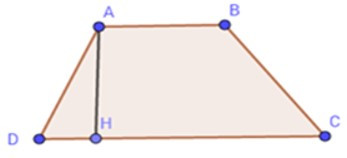
23/07/2024Cho hình thang ABCD, AB song song với CD, đường cao AH.
Biết AB = 7cm; CD = 10cm, diện tích của ABCD là 25,5cm2 thì độ dài AH là:
Xem đáp án
Đáp án: B
Giải thích:
Lời giải
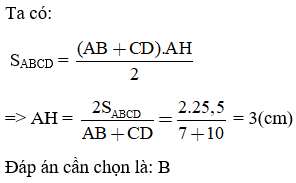
Câu 14:
16/07/2024Cho hình chữ nhật ABCD. Trên cạnh AB lấy M. Tìm vị trí của M để
SMBC = SABCD.
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
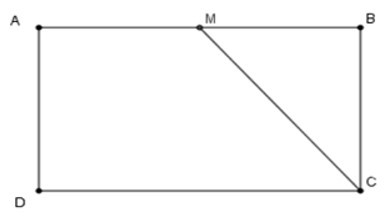
Ta có SABCD = AB.BC;
SMBC = MB.BC
Để SMBC = SABCD
MB.BC = AB.BC
MB = AB
Mà M Є AB nên M là trung điểm đoạn AB.
Câu 15:
17/07/2024Cho tam giác ABC, = 900, AB = 6cm, AC = 8cm.
Hạ AH ⊥ BC, qua H kẻ HE ⊥ AB, HF ⊥ AC với E ЄAB; F Є AC.
1. Tính BC, EF.
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
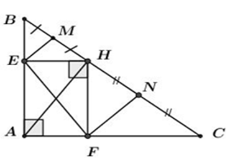
Áp dụng định lý Pitago trong tam giác ABC vuông tại A ta có:
Áp dụng định lý Pitago trong tam giác ABH vuông tại A ta có:
AH2 = AB2 – BH2 = 36 – BH2.
Áp dụng định lý Pitago trong tam giác ACH vuông tại A ta có:
AH2 = AC2 – HC2 = 64 – HC2
=> 36 – BH2 = 64 – HC2
36 – BH2 = 64 – (10 – BH)2 (do HC + BH = BC = 10)
28 – 100 +20BH – BH2 + BH2 = 0
20BH = 72
BH = 3,6
Xét tứ giác AEHF có: = 900 (gt)
=> AEHF là hình chữ nhật (dhnb)
=> AH = EF (hai đường chéo hình chữ nhật bằng nhau)
=> EF = AH = 4,8 cm
Câu 16:
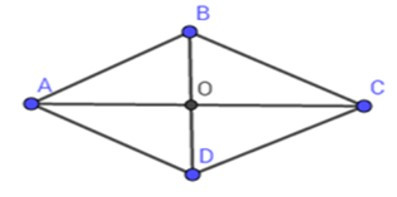
23/07/2024Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O.
Biết OA = 12cm, diện tích hình thoi ABCD là 168cm2. Cạnh của hình thoi là:
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
Câu 17:
21/07/2024Cho hình thang ABCD, đường cao ứng với cạnh DC là AH = 6cm; cạnh DC = 12cm. Diện tích của hình bình hành ABCD là:
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
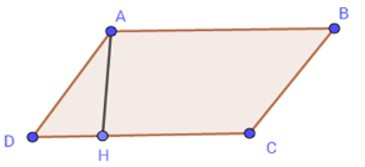
Ta có: SABCD = AH.CD
= 6.12 = 72(cm2)
Câu 18:
21/07/2024Tính diện tích của tam giác đều ABC biết chu vi tam giác ABC bằng 18cm.
Xem đáp án
Đáp án: C
Giải thích:
Lời giải
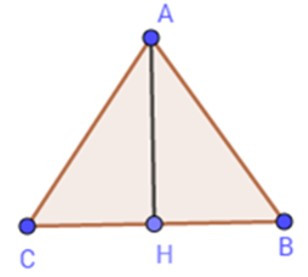
Cạnh của tam giác đều là: AB = BC = CA = 18 : 3 = 6(cm)
Gọi AH là đường cao kẻ từ đỉnh A của tam giác ABC
Khi đó AH vừa là đường cao vừa là đường trung tuyến của tam giác đều ABC.
Suy ra BH = HC = BC = .6 = 3(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AHB ta có:
Câu 19:
16/07/2024Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng
3cm. Gọi M là trung điểm của AB. DM cắt AC tại N.
1. Tính diện tích hình bình hành ABCD, diện tích tam giác ADM.
Xem đáp án
Đáp án: A
Giải thích:
Lời giải
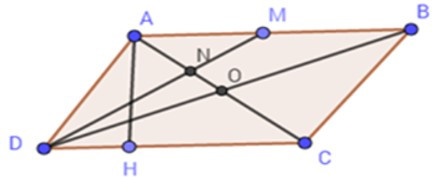
+) SABCD = AH.CD = 4.3 = 12(cm2)
+) Vì M là trung điểm của AB
nên AM = AB = .4 = 2(cm)
Ta có chiều cao từ đỉnh D đến cạnh AM của tam giác ADM bằng chiều cao AH của hình bình hành.
=> SADM = AH.AM
= .3.2 = 3(cm2)
Câu 20:
18/07/2024Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng
3cm. Gọi M là trung điểm của AB. DM cắt AC tại N.
Tính diện tích tam giác AMN.
Xem đáp án
Đáp án: D
Giải thích:
Lời giải
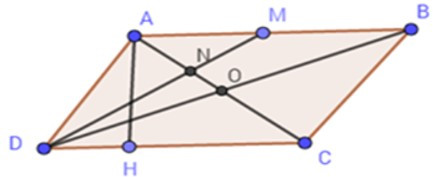
Tứ giác ABCD là hình bình hành nên AC và BD cắt nhau tại trung điểm O của mỗi đường.
Xét tam giác ABD ta có: AO và DM là hai đường trung tuyến của tam giác.
Mà AO DM = {N} => N là trọng tâm tam giác ADB.
=> AN = DM (tính chất đường trung tuyến của tam giác)
Suy ra NM =
+) Hai tam giác AMN và ADM có cùng đường cao hạ từ A nên
Mà theo câu trước SADM = 3 cm2
=> SAMN = SADM = .3 = 1(cm2)