Câu hỏi:
16/07/2024 231Cho hình chữ nhật ABCD. Trên cạnh AB lấy M. Tìm vị trí của M để
SMBC =14 SABCD.
A. M là điểm thuộc đoạn AB sao cho AM = 12 MB
B. M là điểm thuộc đoạn AB sao cho AM = 34 AB
C. M là trung điểm đoạn AB
D. M là điểm thuộc đoạn AB sao cho AM = 12 AB
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án: C
Giải thích:
Lời giải
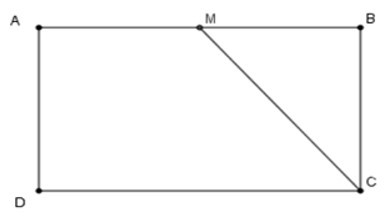
Ta có SABCD = AB.BC;
SMBC = 12MB.BC
Để SMBC = 14SABCD
⇔ 12MB.BC = 14AB.BC
⇔ MB = 14AB
Mà M Є AB nên M là trung điểm đoạn AB.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tính diện tích của tam giác đều ABC biết chu vi tam giác ABC bằng 18cm.
Câu 2:
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O.
Biết OA = 12cm, diện tích hình thoi ABCD là 168cm2. Cạnh của hình thoi là:
Câu 4:
Cho hình thang ABCD, đường cao ứng với cạnh DC là AH = 6cm; cạnh DC = 12cm. Diện tích của hình bình hành ABCD là:
Câu 6:
Một tam giác có độ dài ba cạnh là 12cm, 5cm, 13cm. Diện tích tam giác đó là
Câu 7:
Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng
3cm. Gọi M là trung điểm của AB. DM cắt AC tại N.
1. Tính diện tích hình bình hành ABCD, diện tích tam giác ADM.
Câu 8:
Cho hình bình hành ABCD có CD = 4cm, đường cao vẽ từ A đến cạnh CD bằng
3cm. Gọi M là trung điểm của AB. DM cắt AC tại N.
Tính diện tích tam giác AMN.
Câu 9:
Cho hình thang ABCD, AB song song với CD, đường cao AH.
Biết AB = 7cm; CD = 10cm, diện tích của ABCD là 25,5cm2 thì độ dài AH là:
Câu 11:
Cho hình chữ nhật ABCD có AD = 8cm, AB = 9cm.
Các điểm M, N trên đường chéo BD sao cho BM = MN = ND. Tính diện tích tam giác CMN.
Câu 12:
Hình chữ nhật có diện tích là 240cm2, chiều rộng là 8cm. Chu vi hình chữ nhật đó là:
Câu 14:
Hình chữ nhật có diện tích là 240cm2, chiều rộng là 8cm. Chu vi hình chữ nhật đó là:
Câu 15:
Cho tam giác ABC với ba đường cao AA’, BB’, CC’. Gọi H là trực tâm của tam giác đó. Chọn câu đúng.











