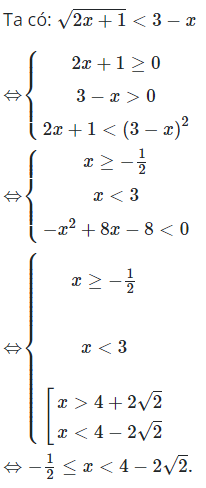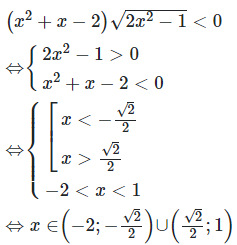Trắc nghiệm Dấu của tam thức bậc hai (có đáp án)
Trắc nghiệm Toán 10 Bài 5: Dấu của tam thức bậc hai
-
545 lượt thi
-
27 câu hỏi
-
45 phút
Danh sách câu hỏi
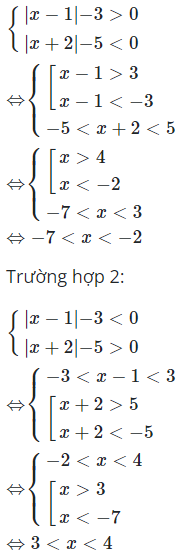
Câu 1:
12/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Lập bảng phá dấu giá trị tuyệt đối giải BPT trong từng khoảng ta được nghiệm là A.
Cách khác:
Trường hợp 1:
Câu 2:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Ta có
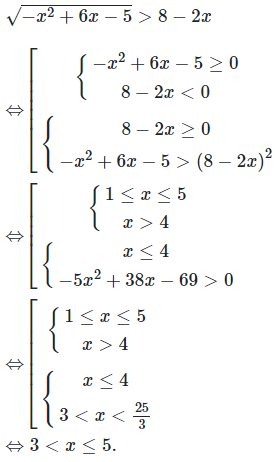
Câu 4:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải
Ta có
Từ (I) và (II) suy ra nghiệm của hệ là .
Câu 5:
11/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Đặt
Ta có
Nếu
thì ta có :
loại
Nếu
thì ta có
loại.
Câu 6:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải
Trường hợp 1: . Khi đó bất phương trình đã cho trở thành , , dấu "=" xảy ra khi .
Trường hợp 2: Khi đó bất phương trình đã cho trở thành .
Giải (1) ta được a >3 (theo bất đẳng thức cauchy).
Giải (2):
Vậy giá trị dương nhỏ nhất của a gần với số 2,6.
Câu 7:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải
Điều kiện
Đặt , điều kiện .
Ta có
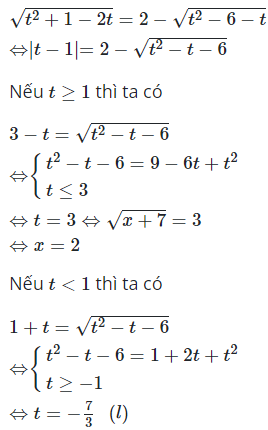
Câu 9:
11/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải
Ta có
Câu 10:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải
Ta có
Hệ số
Áp dụng định lý về dấu của tam thức bậc hai ta có đáp án C là đáp án cần tìm.
Câu 11:
12/12/2024 Xem đáp án
Xem đáp án
Đáp án đúng là : C
Lời giải
Tam thức có 1 nghiệm x=3 và hệ số
*Phương pháp giải:
Đạo hàm tìm nghiệm
Xác định dấu của hệ số a
*Lý thuyết:
1. Dấu của tam thức bậc hai
Tam thức bậc hai (đối với x) là biểu thức có dạng ax2 + bx + c, trong đó a, b, c là những số thực cho trước (với a ≠ 0), được gọi là các hệ số của tam thức bậc hai.
Chú ý : Nghiệm của phương trình bậc hai ax2 + bx + c = 0 cũng là nghiệm của tam thức bậc hai ax2 + bx + c.
Định lí về dấu của tam thức bậc hai
Cho tam thức bậc hai f(x) = ax2 + bx + c (a ≠ 0).
+ Nếu ∆ < 0 thì f(x) cùng dấu với hệ số a với mọi x ∈ℝ.
+ Nếu ∆ = 0 thì f(x) cùng dấu với hệ số a với mọi và
+ Nếu ∆ > 0 thì tam thức f(x) có hai nghiệm phân biệt x1 và x2 (x1 < x2). Khi đó, f(x) cùng dấu với hệ số a với mọi x ∈ (–∞; x1) ∪ (x2; +∞); f(x) trái dấu với hệ số a với mọi x ∈ (x1; x2).
Tức là, khi ∆ > 0, dấu của f(x) và a là: “Trong trái, ngoài cùng”
Chú ý: Trong định lí về dấu của tam thức bậc hai có thể thay ∆ bởi ∆’.
Xem thêm
Lý thuyết Dấu của tam thức bậc hai - Toán 10 Kết nối tri thứcCâu 12:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải
Nếu thì
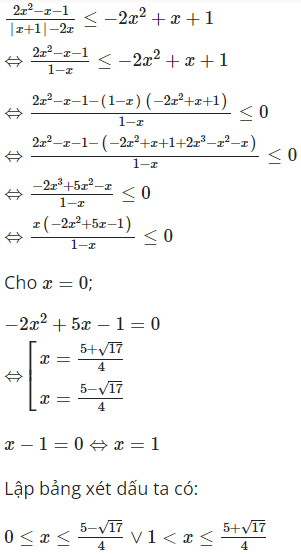
Vì là nghiệm nguyên nên có nghiệm là 0;2.
Nếu thì
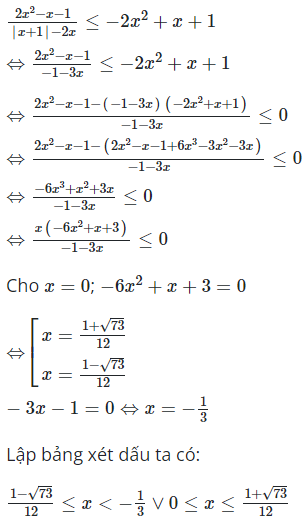
Vì là nghiệm nguyên nên có nghiệm là 0 (loại)
Vậy bất phương trình đã cho có 2 nghiệm nguyên.
Câu 13:
19/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Ta có (1) có hai nghiệm phân biệt khi
Câu 14:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải
Điều kiện
Vậy tập xác định của hàm số là
Câu 15:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải
Để tam thức đổi dấu 2 lần khi và chỉ khi
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải
Điều kiện
Vậy tập xác định của hàm số là
Câu 17:
23/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải
Ta có bảng xét dấu
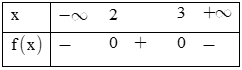
Vậy với và với x <2 hoặc x >3.
Câu 18:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: B
Giải thích:
Hướng dẫn giải
Ta có:
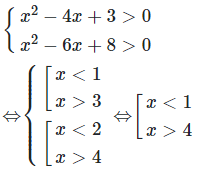
Câu 19:
18/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Ta có:
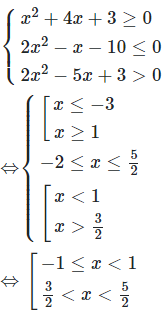
Câu 20:
13/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Ta có:
có tập nghiệm là R khi hệ sau có tập nghiệm là R
(do )
có tập nghiệm là R
Ta có (1) có tập nghiệm là R khi :
(3)
(2) có tập nghiệm là R khi
(4)
Từ (2) và (4), ta có
Câu 21:
21/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải
Xét
Với , ta có:
Với , ta có:
Đặt
Bảng biến thiên:
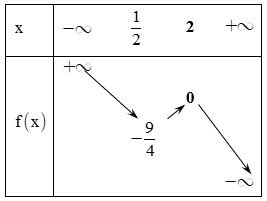
Dựa vào bảng biến thiên ta có .
Câu 22:
20/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải
Xét phương trình:
(1)
Xét
Bảng biến thiên:
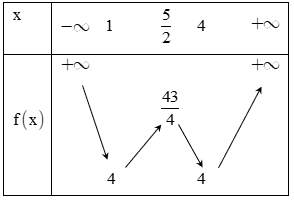
Câu 23:
22/07/2024Để phương trình sau có nghiệm duy nhất: , Giá trị của tham số a là:
 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Xét phương trình:

Câu 24:
14/07/2024 Xem đáp án
Xem đáp án
Đáp án: C
Giải thích:
Hướng dẫn giải
Ta thấy để :
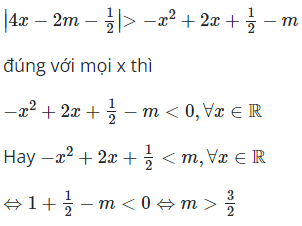
Câu 25:
15/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải
Ta có
Do vế trái luôn lớn hơn hoặc bằng 0 nên để BPT có nghiệm thì nên B đúng.
Với BPT vô nghiệm hay BPT có nghiệm khi nên A đúng.
Khi ta có
có 4 nghiệm xếp thứ tự
Với hoặc ta có BPT:
Có nghiệm và
Nên tồn tại nghiệm lớn hơn 1 vậy C đúng
Câu 26:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: D
Giải thích:
Hướng dẫn giải
Ta có:
có nghiệm khi và chỉ khi
Câu 27:
22/07/2024 Xem đáp án
Xem đáp án
Đáp án: A
Giải thích:
Hướng dẫn giải
Ta có:
Bất phương trình đã cho có nghiệm khi
luôn đúng với .
Có thể bạn quan tâm
- Trắc nghiệm Dấu của tam thức bậc hai (có đáp án) (544 lượt thi)
- Trắc nghiệm Dấu của tam thức bậc hai có đáp án (314 lượt thi)
- Trắc nghiệm Dấu của tam thức bậc hai có đáp án (Nhận biết) (386 lượt thi)
- Trắc nghiệm Dấu của tam thức bậc hai có đáp án (Thông hiểu) (411 lượt thi)
- Trắc nghiệm Dấu của tam thức bậc hai có đáp án (Vận dụng) (248 lượt thi)
- Trắc nghiệm Dấu của tam thức bậc hai có đáp án (Tổng hợp) (339 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn (có đáp án) (2156 lượt thi)
- 75 câu trắc nghiệm Bất đẳng thức - Bất phương trình nâng cao (1180 lượt thi)
- Trắc nghiệm Dấu của nhị thức bậc nhất (có đáp án) (557 lượt thi)
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn có đáp án (Vận dụng) (490 lượt thi)
- Trắc nghiệm Bất đẳng thức có đáp án (Nhận biết) (467 lượt thi)
- Trắc nghiệm Bất đẳng thức (có đáp án) (462 lượt thi)
- Trắc nghiệm Bất đẳng thức có đáp án (450 lượt thi)
- Trắc nghiệm Bất phương trình và hệ bất phương trình một ẩn có đáp án (Tổng hợp) (443 lượt thi)
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn có đáp án (Thông hiểu) (423 lượt thi)
- Trắc nghiệm Bất phương trình bậc nhất hai ẩn có đáp án (416 lượt thi)