50 câu hỏi trắc nghiệm thuộc Đề thi thử môn Toán THPT Quốc gia có lời giải (Đề 29)

Cho số phức z = -i(3i+4). Tìm phần thực và phần ảo của số phức z.

A. Phần thực 3 và phần ảo 4i.

B. Phần thực 3 và phần ảo 4.

C. Phần thực 3 và phần ảo -4.

D. Phần thực 3 và phần ảo -4i.

Xem đáp án

Đáp án C

Ta có: $z = - i (3 i + 4) = 3 - 4 i$ nên phần thực 3 và phần ảo -4.

Câu 3:

Cho hàm số y = f(x) có đồ thị (C) như hình vẽ. Tọa độ điểm cực tiểu của (C) là

A. (0;-2)

B. (0;-4)

C. (1;0)

D. (-2;0)

Xem đáp án

Đáp án B

Câu 4:

Gọi l, h, R lần lượt là độ dài đường sinh, chiều cao và bán kính đáy của một hình nón (N). Diện tích toàn phần của hình nón (N) là

A. $S_{T P} = π R l + π R^{2}$

B. $S_{T P} = 2 π R l + 2 π R^{2}$

C. $S_{T P} = π R l + 2 π R^{2}$

D. $S_{T P} = π R h + π R^{2}$

Xem đáp án

Đáp án A

Câu 5:

Trong không gian Oxyz, cho hai véc tơ $\vec{a} = (- 4; 5; - 3)$ và $\vec{b} = (2; - 2; 3)$ . Véc tơ $\vec{x} = \vec{a} + 2 \vec{b}$ có tọa độ là

A. $(- 2; 3; 0)$

B. $(0; 1; - 1)$

C. $(0; 1; 3)$

D. $(- 6; 8; - 3)$

Xem đáp án

Câu 6:

Trong không gian Oxyz, cho mặt phẳng $(P) : x - 3 z + 2 = 0$ . Một vectơ pháp tuyến của mặt phẳng (P) là

A. $\vec{n} = (1; - 3; 0)$

B. $\vec{n} = (1; - 3; - 1)$

C. $\vec{n} = (1; - 3; 1)$

D. $\vec{n} = (1; 0; - 3)$

Xem đáp án

Câu 7:

Cho hàm số bậc hai y = f(x) = x⁴-5x²+4 có đồ thị như hình vẽ bên. Gọi S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x) và trục hoành (miền phẳng được tô đậm trên hình vẽ). Mệnh đề nào sau đây sai?

A. $S = \int_{- 2}^{2} |f (x)| d x$

B. $S = 2 \int_{0}^{2} |f (x)| d x$

C. $S = 2 |\int_{0}^{1} f (x) d x| + 2 |\int_{1}^{2} f (x) d x|$

D. $S = 2 |\int_{0}^{2} f (x) d x|$

Xem đáp án

Câu 8:

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ bên

Hàm số y = f(x) đồng biến trên khoảng nào dưới đây

A. $(- 1; 3)$

B. $(0; + \infty)$

C. $(- 2; 0)$

D. $(- \infty; - 2)$

Xem đáp án

Đáp án C

Từ bảng biến thiên hàm số ta có hàm đồng biến trên khoảng (-2;0).

Câu 9:

Tập xác định của hàm số y = (x²-4x+3)^π là

A. $ℝ \ \{1; 3\}$

B. $(- \infty; 1] \cup [3; + \infty)$

C. $(1; 3)$

D. $(- \infty; 1) \cup (3; + \infty)$

Xem đáp án

Câu 10:

19/07/2024

Hàm số f(x) = 2^3x-1 có đạo hàm

A. $f^{'} (x) = {3.2}^{3 x - 1}$

B. $f^{'} (x) = {3.2}^{3 x - 1} . \ln 2$

C. $f^{'} (x) = (3 x - 1) {.2}^{3 x - 1}$

D. $f^{'} (x) = (3 x - 1) {.2}^{3 x - 1} . \ln 2$

Xem đáp án

Câu 11:

14/07/2024

Số cách sắp xếp 5 học sinh thành một hàng dọc là

A. 1

B. $ℝ$

C. 5

D. 5!

Xem đáp án

Đáp án D

Mỗi cách sắp xếp 5 học sinh là một hoán vị của 5 phần tử. Số các hoán vị là: 5!.

Câu 12:

Cho f(x), g(x) là các hàm số có đạo hàm liên tục trên R, số $k \in ℝ$ và C là một hằng số tùy ý. Xét 4 mệnh đề sau

(I): ${(\int f (x) d x)}^{'} = f (x)$

(II): $\int k f (x) d x = k \int f (x) d x$

(III): $\int [f (x) + g (x)] d x = \int f (x) d x + \int g (x) d x$

(IV): $\int x^{2} d x = \frac{x^{3}}{3} + C$

Số mệnh đề đúng là

A. 1

B. 2

C. 4

D. 3

Xem đáp án

Đáp án D

(II): $\int k f (x) d x = k \int f (x) d x$ sai khi k = 0.

Câu 13:

Đồ thị hàm số $y = \frac{x + 3}{x^{2} - 4}$ có bao nhiêu tiệm cận?

A. 2

B. 1

C. 3

D. 4

Xem đáp án

Đáp án C

Do bậc của tử lớn hơn của mẫu nên đồ thị hàm số có một tiệm cận ngang y=0.

Mà với x=±2 thì x+3≠0 nên đồ thị hàm số có hai tiệm cận đứng.

Câu 14:

Cho khối tứ diện ABCD. Gọi M, N lần lượt là trung điểm của AB và CD (tham khảo hình vẽ bên). Đặt V là thể tích của khối tứ diện ABCD, V₁ là thể tích của khối tứ diện MNBC. Khẳng định nào sau đây đúng?

A. $\frac{V_{1}}{V} = \frac{1}{4}$

B. $\frac{V_{1}}{V} = \frac{1}{2}$

C. $\frac{V_{1}}{V} = \frac{1}{3}$

D. $\frac{V_{1}}{V} = \frac{2}{3}$

Xem đáp án

Câu 15:

Cho biết $\int_{1}^{5} \frac{3 d x}{x^{2} + 3 x} = a \ln 5 + b \ln 2 (a, b \in ℤ)$ . Mệnh đề nào sau đây đúng

A. 2a-b=0

B. a-b=0

C. a+2b=0

D. a+b=0

Xem đáp án

Câu 16:

Cho hàm số $y = \frac{1}{3} x^{3} + 2 x^{2} + (m + 2) x - m$ . Tìm tập hợp S tất cả các giá trị thực của tham số m để hàm số đồng biến trên R.

A. $S = (- \infty; 2]$

B. $S = (- \infty; 2)$

C. $S = [2; + \infty)$

D. $S = (2; + \infty)$

Xem đáp án

Câu 17:

19/07/2024

Cho a = log3, b = ln3. Mệnh đề nào sau đây đúng

A. $\frac{a}{b} = \frac{e}{10}$

B. $10^{a} = e^{b}$

C. $\frac{1}{a} + \frac{1}{b} = \frac{1}{10}$

D. $10^{b} = e^{a}$

Xem đáp án

Câu 18:

Trong không gian Oxyz, cho điểm A(1;-3;2). Gọi M, N, P lần lượt là hình chiếu vuông góc của A lên trục Ox, Oy, Oz. Phương trình mặt phẳng (MNP) là

A. $x - \frac{y}{3} + \frac{z}{2} = 1$

B. $x + \frac{y}{3} + \frac{z}{2} = 1$

C. $x - \frac{y}{3} + \frac{z}{2} = 0$

D. $6 x - 2 y + 3 z + 6 = 0$

Xem đáp án

Câu 19:

Cho hàm số y = f(x) có đạo hàm trên R và $f^{'} (x) > 0, \forall x \in ℝ$ , biết f(3)=1. Chọn mệnh đề đúng

A. $f (4) = 0$

B. $f (2019) > f (2020)$

C. $f (1) = 3$

D. $f (5) + 1 > f (1) + f (2)$

Xem đáp án

Câu 20:

15/07/2024

Với C là một hằng số tùy ý, họ nguyên hàm của hàm số f(x)=2cosx-x là

A. $2 \sin x - \frac{x^{2}}{2} + C$

B. $- 2 \sin x - x^{2} + C$

C. $2 \sin x - 1 + C$

D. $- 2 \sin x - \frac{x^{2}}{2} + C$

Xem đáp án

Câu 21:

Cho khối lăng trụ ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AB=a, BC=2a, A’B vuông góc với mặt phẳng (ABC) và góc giữa A’C và mặt phẳng (ABC) bằng 30° (tham khảo hình vẽ bên). Tính thể tích khối lăng trụ ABC.A’B’C’.

A. $\frac{a^{3}}{3}$

B. $3 a^{3}$

C. $a^{3}$

D. $\frac{a^{3}}{6}$

Xem đáp án

Câu 22:

Cho hàm số y = ax⁴+bx²+c (a≠0) có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng

A. $a > 0, b > 0, c < 0$

B. $a < 0, b > 0, c < 0$

C. $a > 0, b < 0, c < 0$

D. $a > 0, b > 0, c > 0$

Xem đáp án

Câu 23:

Cho hàm số $y = \frac{2 x - 1}{x + 1}$ . Trong các mệnh đề sau, mệnh đề nào sai?

A. Đồ thị hàm số cắt trục hoành tại điểm có hoành độ $x = \frac{1}{2}$

B. Đồ thị hàm số có tiệm cận ngang là: y = 2

C. Hàm số gián đoạn tại x = -1

D. Hàm số đồng biến trên tập xác định của nó

Xem đáp án

Câu 24:

Các bài toán thực tế hình không gian (có đáp án)

Trong không gian Oxzyz, cho hai điểm A(2;-1;4), B(3;2;-1) và mặt phẳng $(P) : x + y + 2 z - 4 = 0$ . Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phương trình là

A. $11 x - 7 y - 2 z + 21 = 0$

B. $11 x + 7 y - 2 z - 7 = 0$

C. $11 x - 7 y - 2 z - 21 = 0$

D. $11 x + 7 y - 2 z + 7 = 0$

Xem đáp án

Câu 25:

09/10/2024

Tính thể tích khối cầu ngoại tiếp hình lập phương có cạnh bằng a

A. $V = \frac{π a^{3} \sqrt{3}}{2}$

B. $V = 4 π a^{3} \sqrt{3}$

C. $V = \frac{π a^{3} \sqrt{3}}{8}$

D. $V = \frac{4 π a^{3} \sqrt{3}}{3}$

Xem đáp án

Đáp án đúng: A

*Phương pháp giải:

- Tính bán kính khối cầu

- Áp dụng công thức tính thể tích khối cầu để tính=

*Lời giải:

*Một số dạng bài và lý thuyết thêm về khối cầu:

Diện tích mặt cầu và thể tích khối cầu

Cho mặt cầu S(I; R).

Diện tích mặt cầu: $S = 4 π R^{2}$

Thể tích khối cầu: $V = \frac{4}{3} π R^{3}$

Dạng 1: Mặt cầu ngoại tiếp hình chóp

* Phương pháp giải:

- Xác định trục d của đường tròn ngoại tiếp đa giác đáy (d là đường thẳng vuông góc với đáy tại tâm đường tròn ngoại tiếp đa giác đáy).

- Xác định mặt phẳng trung trực (P) của một cạnh bên (hoặc trục ∆ của đường tròn ngoại tiếp một đa giác của mặt bên).

- Giao điểm I của (P) và d (hoặc của ∆ và d) là tâm mặt cầu ngoại tiếp.

- Kết luận: I là tâm mặt cầu ngoại tiếp chóp.

Dạng 1.1: Hình chóp có các điểm cùng nhìn một cạnh của hình chóp dưới một góc vuông.

+) Hình chóp tam giác:

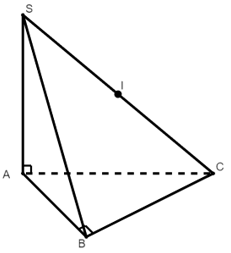
A, B cùng nhìn SC dưới một góc vuông

Tâm mặt cầu ngoại tiếp hình chóp S.ABC là trung điểm I của SC

Bán kính là: $R = \frac{S C}{2}$

+) Hình chóp tứ giác

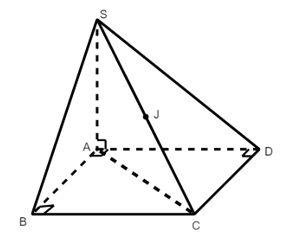
A, B, D cùng nhìn SC dưới một góc vuông

Tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm J của SC

Bán kính mặt cầu là: $R = \frac{S C}{2}$

Dạng 1.2: Hình chóp có mặt bên vuông góc với mặt phẳng đáy

* Phương pháp giải: Gọi h là chiều cao hình chóp và $R_{b}, R_{d}$ là bán kính của đường tròn ngoại tiếp mặt bên, mặt đáy và $\partial$ là độ dài cạnh chung của mặt bên vuông góc với đáy thì bán kính mặt cầu là:

$R = \sqrt{{R_{b}}^{2} + {R_{d}}^{2} - {(\frac{\partial}{2})}^{2}}$

Dạng 1.3: Mặt cầu nội tiếp khối đa diện

* Phương pháp giải: Nếu đặt V là thể tích khối chóp và $S_{t p}$ là tổng diện tích mặt đáy và các mặt bên của chóp thì bán kính r của mặt cầu nội tiếp khối chóp: $r = \frac{3 V}{S_{t p}}$

Xem thêm các bài viết liên quan hay, chi tiết

Bài tập Mặt cầu Toán 12

Phương trình mặt cầu (lý thuyết và cách giải các dạng bài tập)

Câu 26:

Hàm số nào sau đây có bảng biến thiên như hình vẽ bên?

A. $y = \frac{x + 3}{x - 2}$

B. $y = \frac{2 x - 1}{x - 2}$

C. $y = \frac{2 x - 3}{x + 2}$

D. $y = \frac{2 x - 5}{x - 2}$

Xem đáp án

Câu 27:

Gọi A, B lần lượt 2 điểm biểu diễn số phức z₁, z₂ trong mặt phẳng phức ở hình vẽ bên. Tính |z₁-z₂|.

A. $\frac{\sqrt{17}}{2}$

B. $\sqrt{5}$

C. $\sqrt{17}$

D. $\sqrt{29}$

Xem đáp án

Câu 28:

Cho hàm số f(x) = ln(x²-4x+8). Số nghiệm nguyên dương của bất phương trình $f^{'} (x) \leq 0$ là số nào sau đây.

A. 4

B. 2

C. 1

D. 3

Xem đáp án

Câu 29:

Hàm số nào sau đây đồng biến trên tập xác định của nó?

A. $y = {(\frac{3}{π})}^{x}$

B. $y = {(\frac{\sqrt{2} + \sqrt{3}}{e})}^{x}$

C. $y = {(\sqrt{2020} - \sqrt{2019})}^{x}$

D. $y = \log_{\frac{1}{2}} (x + 4)$

Xem đáp án

Câu 30:

Cho cấp số nhân (u_n) có u₁=3, công bội q=-2, biết u_n=192. Tìm n?

A. n=7

B. n=5

C. n=6

D. n=8

Xem đáp án

Câu 31:

Trong không gian Oxyz, tìm phương trình mặt cầu (S) có tâm I(1;-4;2) và diện tích 64π

A. ${(x - 1)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 4$

B. ${(x + 1)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 16$

C. ${(x - 1)}^{2} + {(y - 4)}^{2} + {(z + 2)}^{2} = 4$

D. ${(x - 1)}^{2} + {(y + 4)}^{2} + {(z - 2)}^{2} = 16$

Xem đáp án

Câu 32:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 1}{2} = \frac{y}{- 1} = \frac{z - 2}{1}$ và mặt phẳng $(P) : x + y + 2 z - 1 = 0$ . Góc giữa đường thẳng d và mặt phẳng (P) bằng

A. 60°

B. 30°

C. 45°

D. 90°

Xem đáp án

Câu 33:

Cho hàm số f(x) = 3^x-3^-x, với m₁, m₂ là các giá trị thực của tham số m sao cho $f (3 \log_{2} m) + f (\log_{2}^{2} m + 2) = 0$ . Tính T=m₁m₂.

A. $T = \frac{1}{8}$

B. $T = \frac{1}{4}$

C. $T = \frac{1}{2}$

D. $T = 2$

Xem đáp án

Câu 34:

Cho hàm số f(x) có đạo hàm liên tục trên đoạn [2;3] và $\int_{2}^{3} (x - 2) f^{'} (x) d x = a$ , $f (3) = b$ . Tìm tích phân $\int_{2}^{3} f (x) d x$ theo a và b.

A. -a-b

B. b-a

C. a-b

D. a+b

Xem đáp án

Câu 35:

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B; AB=BC=1, AD=2. Các mặt chéo (SAC) và (SBD) cùng vuông góc với mặt đáy (ABCD). Biết góc giữa hai mặt phẳng (SAB) và (ABCD) bằng 60° (tham khảo hình vẽ bên). Khoảng cách từ điểm D đến mặt phẳng (SAB) là

A. $\frac{2 \sqrt{3}}{3}$

B. $\sqrt{3}$

C. $2 \sqrt{3}$

D. $\frac{\sqrt{3}}{3}$

Xem đáp án

Câu 36:

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ

Phương trình $|f (1 - 2 x) + 2| = 5$ có tất cả bao nhiêu nghiệm thực phân biệt

A. 5

B. 4

C. 3

D. 6

Xem đáp án

Câu 37:

14/07/2024

Cho hàm số y = f(x). Hàm số y = f’(x) là hàm số bậc ba có đồ thị như hình vẽ bên.

Hàm số $y = f (3 - e^{x})$ đồng biến trên khoảng nào dưới đây?

A. $(2; + \infty)$

B. $(- \infty; 1)$

C. $(\ln 2; \ln 4)$

D. $(\ln 2; 4)$

Xem đáp án

Câu 38:

Cho số phức $z = a + b i (a, b \in ℝ)$ thỏa mãn $z - (2 + 3 i) \bar{z} = 1 - 9 i$ . Tính T=ab+1

A. T=-2

B. T=0

C. T=1

D. T=-1

Xem đáp án

Câu 39:

Một hộp chứa 5 bi trắng, 6 bi đỏ và 7 bi xanh, tất cả các bi có kích thước và khối lượng như nhau. Chọn ngẫu nhiên 6 bi từ hộp đó. Tính xác suất để 6 bi lấy được có đủ ba màu đồng thời hiệu của số bi đỏ và trắng, hiệu của số bi xanh và đỏ, hiệu của số bi trắng và xanh theo thứ tự lập thành cấp số cộng

A. $\frac{5}{442}$

B. $\frac{75}{442}$

C. $\frac{40}{221}$

D. $\frac{35}{221}$

Xem đáp án

Câu 40:

Cho hình lục giác đều ABCDEF có cạnh bằng 2 (tham khảo hình vẽ). Quay lục giác xung quanh đường chéo AD ta được một khối tròn xoay. Thể tích khối tròn xoay đó là

A. $V = 8 π$

B. $V = 7 π$

C. $V = \frac{8 π \sqrt{3}}{3}$

D. $V = \frac{7 π \sqrt{3}}{3}$

Xem đáp án

Câu 41:

Cho hàm số $f (x) = x^{3} - x^{2} + x - m - 2$ (m là tham số thực). Gọi S là tập hợp tất cả các giá trị của m sao cho $\max_{[0; 3]} |f (x)| + \min_{[0; 3]} |f (x)| = 16$ . Tổng các phần tử của S là

A. 3

B. 17

C. 34

D. 31

Xem đáp án

Câu 42:

Trong không gian Oxyz, cho đường thẳng $d : \frac{x - 2}{1} = \frac{y - 4}{2} = \frac{z - 5}{2}$ và mặt phẳng $(P) : 2 x + z - 5 = 0$ . Đường thẳng nằm trong mặt phẳng (P), cắt và vuông góc với đường thẳng $d$ có phương trình là

A. $\frac{x - 1}{2} = \frac{y - 2}{- 3} = \frac{z - 3}{- 4}$

B. $\frac{x - 1}{2} = \frac{y - 2}{5} = \frac{z - 3}{- 4}$

C. $\frac{x - 1}{2} = \frac{y - 2}{3} = \frac{z - 3}{- 4}$

D. $\frac{x - 1}{2} = \frac{y - 2}{- 5} = \frac{z - 3}{- 4}$

Xem đáp án

Câu 43:

Dân số hiện nay của tỉnh là 1,8 triệu người. Biết rằng trong 10 năm tiếp theo, tỷ lệ tăng dân số bình quân hàng năm của tỉnh X luôn giữ mức 1,4%. Dân số của tỉnh X sau 5 năm (tính từ hiện nay) gần nhất với số liệu nào sau đây?

A. 1,9 triệu người.

B. 2,2 triệu người.

C. 2,1 triệu người.

D. 2,4 triệu người.

Xem đáp án

Câu 44:

Cho hàm số y = f(x) có đạo hàm cấp hai liên tục trên R. Biết $f^{'} (- 2) = - 8, f^{'} (1) = 4$ và đồ thị hàm số f”(x) như hình vẽ dưới đây. Hàm số $y = 2 f (x - 3) + 16 x + 1$ đạt giá trị lớn nhất tại x₀ thuộc khoảng nào sau đây?

A. $(0; 4)$

B. $(4; + \infty)$

C. $(- \infty; 1)$

D. $(- 2; 1)$

Xem đáp án

Câu 45:

16/07/2024

Cho hàm số f(x) thỏa mãn f(-2) = -2; f(2) = 2 và có bảng biến thiên như sau

Có bao nhiêu số tự nhiên m để bất phương trình $f (- f (x)) \geq m$ có nghiệm trên [-1;1].

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Câu 46:

Cho 3 số phức z, z₁, z₂ thỏa mãn $|z - 1 + 2 i| = |z + 3 - 4 i|$ , $|z_{1} + 5 - 2 i| = 2$ , $|z_{2} - 1 - 6 i| = 2$ . Tính giá trị nhỏ nhất của biểu thức $T = |z - z_{1}| + |z - z_{2}| + 4$ .

A. $\frac{2 \sqrt{3770}}{13}$

B. $\frac{\sqrt{10361}}{13}$

C. $\frac{\sqrt{3770}}{13}$

D. $\frac{\sqrt{10361}}{26}$

Xem đáp án

Câu 47:

19/07/2024

Trong không gian Oxyz, cho hai điểm A(1;1;3), B(5;2;-1) và hai điểm M, N thay đổi trên mặt phẳng (Oxy) sao cho điểm I(1;2;0) luôn là trung điểm của MN. Khi biểu thức $P = M A^{2} + 2 N B^{2} + \bar{M A} . \bar{N B}$ đạt giá trị nhỏ nhất. Tính $T = 2 x_{M} - 4 x_{N} + 7 y_{M} - y_{N}$ .

A. T=-10

B. T=-12

C. T=-11

D. T=-9

Xem đáp án

Câu 48:

Cho hình lập phương ABCD.A₁B₁C₁D₁ có cạnh bằng 1. Hai điểm M, N lần lượt thay đổi trên các đoạn AB₁ và BC₁ sao cho MN luôn tạo với mặt phẳng (ABCD) một góc 60° (tham khảo hình vẽ). Giá trị bé nhất của đoạn MN là

A. $\frac{\sqrt{3}}{3}$

B. $2 (\sqrt{2} - 1)$

C. $2 (\sqrt{3} - \sqrt{2})$

D. $\sqrt{3} - 1$

Xem đáp án

Câu 49:

Tính T = a-3b biết hàm số y=f(x) liên tục và có đạo hàm trên R thỏa mãn $3 f^{2} (x) . f^{'} (x) - 4 x e^{- f^{3} (x) + 2 x^{2} + x + 1} = 1 = f (0)$ . Biết rằng $I = \int_{0}^{\frac{- 1 + \sqrt{4089}}{4}} (4 x + 1) f (x) d x = \frac{a}{b}$ là phân số tối giản.

A. T=6123

B. T=12279

C. T=6125

D. T=12273

Xem đáp án

Câu 50: