70 câu trắc nghiệm Khối đa diện cơ bản (P1)
70 câu trắc nghiệm Khối đa diện cơ bản (P1)
-
580 lượt thi
-
30 câu hỏi
-
25 phút
Danh sách câu hỏi
Câu 1:
23/07/2024Mỗi hình sau gồm một số hữu hạn đa giác, tìm hình không phải là hình đa diện.
 Xem đáp án
Xem đáp án
Đáp án D
Hình sau không là hình đa diện vì có một cạnh là cạnh của nhiều hơn 2 mặt
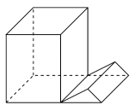
Câu 2:
16/10/2024Hình nào dưới đây không phải là hình đa diện?
 Xem đáp án
Xem đáp án
Đáp án đúng: C
*Phương pháp giải:
- Nắm kỹ về khái niệm, tính chất của hình đa diện: Nhận diện được hình, số đỉnh, số cạnh, số mặt,...của hình đa diện
*Lời giải:
Hình đa diện là hình được tạo bởi một số hữu hạn các đa giác thỏa mãn hai tính chất:
a. Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
b. Mỗi cạnh của đa giác là cạnh chung của đúng hai đa giác.
Mỗi đa giác như trên được gọi là một mặt của hình đa diện
Hình sau không phải là hình đa diện vì có một cạnh là cạnh chung của ba mặt.
*Lý thuyết nắm thêm về hình đa diện và khối đa diện
+) Hai đa diện bằng nhau: hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
+) Khối đa diện đều:
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
+) Thể tích khối đa diện:
- Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.
+) Thể tích khối lăng trụ:
- Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h
+) Thể tích khối chóp:
- Thể tích khối chóp có diện tích đáy B và chiều cao h là: V =
Xem thêm các bài viết liên quan hay, chi tiết:
Câu 3:
19/07/2024Hình nào không phải là hình đa diện đều trong các hình dưới đây?
 Xem đáp án
Xem đáp án
Đáp án D
Hình chóp tam giác đều chỉ biết mặt đáy là tam giác đều nhưng các mặt bên chưa chắc là tam giác đều.
Câu 4:
20/07/2024Trong các mệnh đề sau, hãy chọn mệnh đề đúng. Trong một khối đa diện thì:
 Xem đáp án
Xem đáp án
Đáp án D
Trong khối đa diện thì mỗi đỉnh là đỉnh chung của ít nhất ba cạnh nên nó là đỉnh chung của ít nhất ba mặt
Câu 5:
22/07/2024Tổng độ dài l của tất cả các cạnh của một hình lập phương cạnh a.
 Xem đáp án
Xem đáp án
Đáp án B
Hình lập phương có tất cả 12 cạnh nên l = 12a.
Câu 6:
22/07/2024Cho các hình vẽ sau:
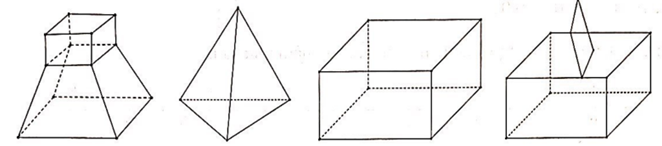
Số các hình đa diện trong các hình trên là:
 Xem đáp án
Xem đáp án
Đáp án A
Dựa vào tính chất hình đa diện thì chỉ có hình thứ 4 ( từ bên trái sang ) không là hình đa diện. Do đó có 3 hình là hình đa diện
Câu 7:
23/07/2024Mỗi đỉnh của một đa diện là đỉnh chung của ít nhất bao nhiêu mặt?
 Xem đáp án
Xem đáp án
Đáp án A
Theo định nghĩa của đa diện, mỗi đỉnh của đa diện là đỉnh chung của ít nhất 3 mặt.
Câu 8:
28/11/2024Cho một hình đa diện. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng: D
*Lời giải
Hình đa diện có tính chất: Mỗi cạnh là cạnh chung của đúng hai mặt.
*Phương pháp giải
Một khối đa diện lồi được gọi là khối đa diện đều loại {p,q}
- Mỗi mặt của nó là một đa giác đều p cạnh
- Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
*Lý thuyến cần nắm và dạng toán về khối đa diện:
- Khối đa diện là phần không gian được giới hạn bởi một hình đa diện, kể cả hình đa diện đó.
- Những điểm không thuộc khối đa diện được gọi là điểm ngoài của khối đa diện. Những điểm thuộc khối đa diện nhưng không thuộc hình đa diện giới hạn khối đa diện ấy được gọi là điểm trong của khối đa diện.
Tập hợp các điểm trong được gọi là miền trong, tập hợp các điểm ngoài được gọi là miền ngoài của khối đa diện.
- Mỗi hình đa diện chia các điểm còn lại của không gian thành hai miền không giao nhau là miền trong và miền ngoài của hình đa diện, trong đó chỉ có miền ngoài là chứa hoàn toàn một đường thẳng nào đấy.
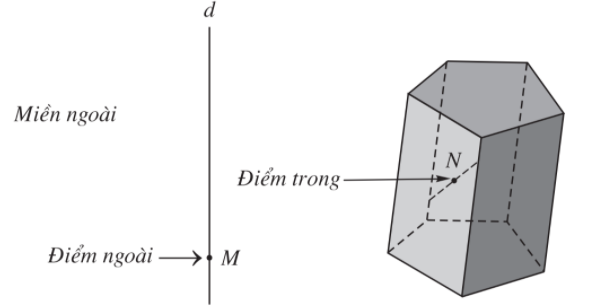
Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
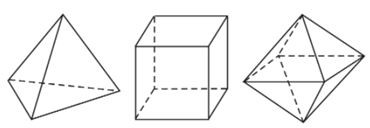
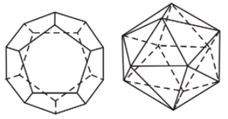
Bảng tóm tắt của năm loại khối đa diện đều.

Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Khối đa diện lồi và khối đa diện đều
50 Bài tập Khái niệm về khối đa diện
50 bài toán về thể tích khối đa diện (có đáp án 2024) – Toán 12
Câu 9:
22/07/2024Chọn khẳng định sai. Trong một khối đa diện
 Xem đáp án
Xem đáp án
Đáp án B
Trong hình hộp chữ nhật, 2 mặt đối diện không có điểm chung. Cho nên, 2 mặt bất kỳ trong khối đa diện chưa chắc đã có điểm chung
Câu 10:
13/07/2024Số đỉnh của hình hai mươi mặt đều là:
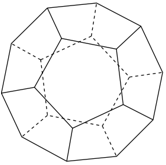
 Xem đáp án
Xem đáp án
Đáp án B
Số đỉnh của hình mười hai mặt đều là 20 đỉnh
Câu 11:
20/07/2024Hình đa diện trong hình vẽ dưới có bao nhiêu mặt:
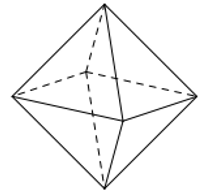
 Xem đáp án
Xem đáp án
Đáp án C
Hình đa diện đã cho có tất cả 8 mặt.
Câu 12:
22/07/2024Trong không gian chỉ có 5 loại khối đa diện đều.
Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án A
Quan sát hình minh họa các khối đa diện đều ta thấy khối lập phương và khối bát diện đều cùng có 12 cạnh.
Câu 14:
13/07/2024Trong các mệnh đề sau, mệnh đề nào sai?
 Xem đáp án
Xem đáp án
Đáp án B
Lắp ghép 2 khối hộp chưa chắc được 1 khối đa diện lồi
Câu 15:
17/07/2024Mặt phẳng nào sau đây chia khối hộp ABCD.A'B'C'D' thành hai khối lăng trụ?
 Xem đáp án
Xem đáp án
Đáp án B
Mặt phẳng (ABC') chia khối hộp ABCD.A'B'C'D' thành 2 khối lăng trụ BB'C'.AA'D' và BCC'.ADD'
Câu 16:
01/12/2024Trong các khối đa diện đều sau, khối đa diện đều nào là khối đa diện đều loại {4;3}?
 Xem đáp án
Xem đáp án
Đáp án đúng là A
Lời giải
Khối đa diện đều loại {p,q} là khối đa diện mà
“Mỗi mặt của đa diện có p cạnh” và “Mỗi đỉnh của đa diện là đỉnh chung của q mặt”
Vậy khối đa diện đều loại {4,3} là khối có mặt là tứ giác và mỗi đỉnh là đỉnh chung của ba mặt, nên là khối lập phương.
*Phương pháp giải:
- Nắm lại kiến thức về khối đa diện đều: định nghĩa, định lý( xác định số mặt, số đỉnh và loại đa diện đều), công thức tính diện tích và thể tích các khối đa diện đều
* Lý thuyết
a). Tứ diện : đều cạnh
Ta có và
Do đó

b) Hình lập phương cạnh Khối lập phương có thể tích .
c) Khối bát diện đều cạnh , ta có
và
Do đó

Xem thêm
Bài tập Khái niệm về khối đa diện Toán 12
Bài tập Khối đa diện lồi và khối đa diện đều Toán 12
Câu 17:
21/07/2024Khối đa diện đều nào thuộc loại {5; 3}?
 Xem đáp án
Xem đáp án
Đáp án C
Khối 12 mặt đều có mỗi mặt là ngũ giác đều và mỗi đỉnh là đỉnh chung của đúng ba mặt, nên thuộc loại {5; 3}.
Câu 18:
22/07/2024Khối mười hai mặt đều là khối đa diện loại nào?
 Xem đáp án
Xem đáp án
Đáp án D
Khối mười hai mặt đều mỗi mặt có 5 cạnh và mỗi đỉnh là chung của 3 mặt nên là loại {5;3}.
Câu 19:
20/07/2024Khối bát diện đều thuộc loại:
 Xem đáp án
Xem đáp án
Đáp án D
Khối bát diện đều thuộc loại {3;4}.
Câu 20:
20/07/2024Một hình chóp ngũ giác đều có bao nhiêu mặt và bao nhiêu cạnh?
 Xem đáp án
Xem đáp án
Đáp án D
Một hình chóp ngũ giác đều có 6 mặt và 10 cạnh.
Câu 21:
21/07/2024Có bao nhiêu loại khối đa diện đều?
 Xem đáp án
Xem đáp án
Đáp án A
Có năm khối đa diện đều: Tứ diện đều, hình lập phương, bát diện đều, thập nhị diện đều, nhị thập diện đều.
Câu 22:
20/07/2024Hình đa diện đều nào dưới đây có tất cả các mặt không phải là tam giác đều?
 Xem đáp án
Xem đáp án
Đáp án C
Hình 12 mặt đều có 12 mặt là các ngũ giác đều.
Câu 23:
21/07/2024Giá trị |p-q| của khối đa diện lồi đều loại {p;q} không thể bằng:
 Xem đáp án
Xem đáp án
Đáp án D
Có 5 loại khối đa diện lồi, đều là {3;3}, {3;4}, {4;3}, {3;5}, {5;3} nên giá trị |p-q| chỉ có thể là 0, 1, 2.
Câu 24:
21/07/2024Trong tất cả các loại hình đa diện đều sau đây, hình nào có số mặt nhiều nhất?
 Xem đáp án
Xem đáp án
Đáp án D
Hình đa diện đều loại {3;5} có 20 mặt, là hình đa diện đều có số mặt nhiều nhất.
Câu 25:
18/07/2024Thể tích V của khối lăng trụ có chiều cao bằng h và diện tích đáy bằng B là:
 Xem đáp án
Xem đáp án
Đáp án A
Thể tích khối lăng trụ: V = Bh.
Câu 26:
23/07/2024Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác cân tại A, và . Tính theo a thể tích V của khối lăng trụ ABC.A'B'C'
 Xem đáp án
Xem đáp án
Đáp án D
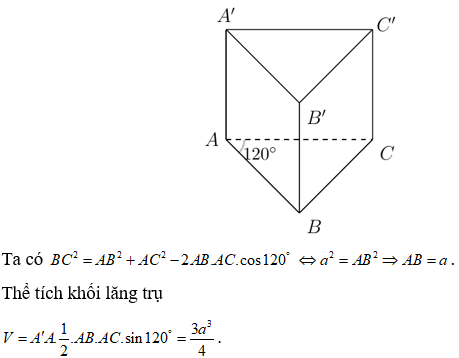
Câu 27:
22/07/2024Cho khối lăng trụ tam giác đứng ABC.A'B'C' có đáy là tam giác vuông tại A, AC = AB = 2a, góc giữa AC' và mặt phẳng (ABC) bằng 300. Tính thể tích của khối lăng trụ ABC.A'B'C'
 Xem đáp án
Xem đáp án
Đáp án D

Câu 28:
13/07/2024Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
 Xem đáp án
Xem đáp án
Đáp án C
Gọi H là trung điểm của AC
Theo đầu bài suy ra
Xét vuông cân tại B, ta có:
Ta có BH là hình chiếu của SB xuống mặt phẳng (ABC) nên
Thể tích của hình chóp SABC là:
Câu 29:
22/07/2024Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh . Cạnh bên SA vuông góc với mặt phẳng (ABCD) và SC=4a. Tìm thể tích khối chóp S.ABCD
 Xem đáp án
Xem đáp án
Đáp án D
Xét vuông tại B, ta có:
Diện tích đáy ABCD là:
Xét vuông tại A, ta có:
Thể tích hình chóp SABCD là:
Câu 30:
13/07/2024Cho khối chóp S.ABCD có đáy là hình chữ nhật cạnh AB=3a, BC=a. Cạnh bên SA vuông góc với đáy; SC tạo với mặt phẳng (ABCD) một góc 600. Tính thể tích V của khối chóp đã cho
 Xem đáp án
Xem đáp án
Đáp án C
Xét vuông tại B, ta có:
Ta có , do đó AC là hình chiếu của SC xuống mặt phẳng (ABCD)
Xét vuông tại A, ta có:
Thể tích hình chóp SABCD là:
Có thể bạn quan tâm
- Trắc nghiệm Ôn tập Chương 1 - Khối đa diện (có đáp án) (520 lượt thi)
- 70 câu trắc nghiệm Khối đa diện cơ bản (P1) (579 lượt thi)
- 80 câu trắc nghiệm Khối đa diện nâng cao (P1) (373 lượt thi)
- 20 câu trắc nghiệm: Ôn tập chương 1 Hình học 12 có đáp án (343 lượt thi)
- Trắc nghiệm Ôn tập chương có đáp án (Nhận biết) (331 lượt thi)
- Trắc nghiệm Ôn tập chương có đáp án (Thông hiểu) (380 lượt thi)
- Trắc nghiệm Ôn tập chương có đáp án (Vận dụng) (360 lượt thi)
- Trắc nghiệm Ôn tập chương có đáp án (Vận dụng) (319 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Khái niệm về khối đa diện (có đáp án) (808 lượt thi)
- 19 câu trắc nghiệm: Khái niệm về khối đa diện có đáp án (554 lượt thi)
- Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án (Nhận biết) (504 lượt thi)
- Trắc nghiệm Khối đa diện lồi và khối đa diện đều (có đáp án) (474 lượt thi)
- Trắc nghiệm Khái niệm về khối đa diện có đáp án (Vận dụng) (468 lượt thi)
- Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng) (461 lượt thi)
- Trắc nghiệm Khái niệm về khối đa diện có đáp án (Thông hiểu) (433 lượt thi)
- Trắc nghiệm Khái niệm về thể tích của khối đa diện (có đáp án) (422 lượt thi)
- Trắc nghiệm Khái niệm về khối đa diện (nhận biết) (405 lượt thi)
- Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án (Vận dụng) (392 lượt thi)
