Trắc nghiệm Khái niệm về thể tích của khối đa diện (có đáp án)
Trắc nghiệm Toán 12 Bài 3: Khái niệm về thể tích của khối đa diện
-
448 lượt thi
-
25 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
23/07/2024 Xem đáp án
Xem đáp án
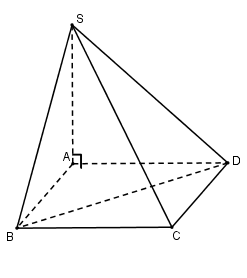
Ta có:
SΔBCD=12SABCD=12a2
VS.BCD=13SA.SBCD
=13a.12a2=a36
Đáp án cần chọn là: A
Câu 2:
20/07/2024 Xem đáp án
Xem đáp án
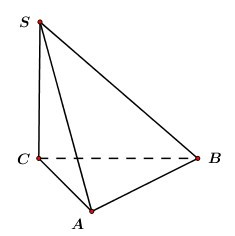
Ta có:
SABC=12AB2=12a2
⇒VS.ABC=13SC.SABC
=13.3a.12a2=12a3
Đáp án cần chọn là: C
Câu 3:
13/07/2024 Xem đáp án
Xem đáp án
Công thức tính thể tích khối chóp V=13Sh
Đáp án cần chọn là: C
Câu 4:
21/07/2024 Xem đáp án
Xem đáp án
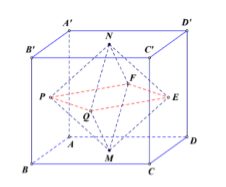
Đặc biệt hóa, coi ABCD.A’B’C’D’ là khối lập phương cạnh bằng 1
⇒VABCD.A'B'C'D'=1=V
Dễ thấy PQEFNM là khối bát diện đều cạnh
QE=12BD=√22
Vậy
VPQEFNM=(√22)3√23=16=V6
Đáp án cần chọn là: C
Câu 5:
21/07/2024 Xem đáp án
Xem đáp án
Nếu A’, B’, C’ là ba điểm lần lượt nằm trên các cạnh SA, SB, SC của hình chóp tam giác S.ABC thì:
VS.A'B'C'VS.ABC=SA'SA.SB'SB.SC'SC
Câu 6:
23/07/2024 Xem đáp án
Xem đáp án
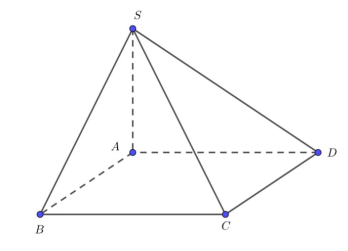
Thể tích khối chóp đã cho là:
VSABCD=13SA.SABCD
=13.3a.a2=a3
Đáp án cần chọn là: A
Câu 7:
17/07/2024 Xem đáp án
Xem đáp án
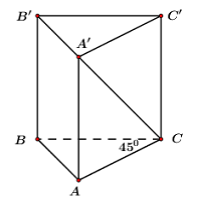
Ta có: cân tại C
Áp dụng định lí Pitago cho vuông tại A ta có:
Đáp án cần chọn là: B
Câu 8:
21/07/2024 Xem đáp án
Xem đáp án
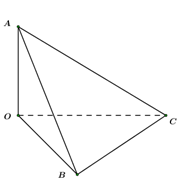
Thể tích khối đa diện OABC là:
Đáp án cần chọn là: D
Câu 9:
23/07/2024 Xem đáp án
Xem đáp án
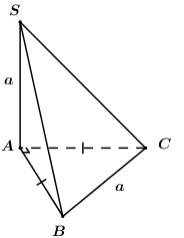
Ta có tam giác ABC vuông cân tại A và
Khi đó:
Vậy thể tích khối chóp S.ABC là:
Đáp án cần chọn là: B
Câu 10:
13/07/2024 Xem đáp án
Xem đáp án
Diện tích toàn phần của hình hộp chữ nhật:
Thể tích hình hộp chữ nhật:
V = abh
Thể tích của lăng trụ là:
Diện tích toàn phần của khối lập phương:
Thể tích của khối lập phương:
Thể tích khối chóp là:
Do đó các đáp án B, C, D đúng, chỉ có A sai.
Đáp án cần chọn là: A
Câu 11:
15/07/2024 Xem đáp án
Xem đáp án
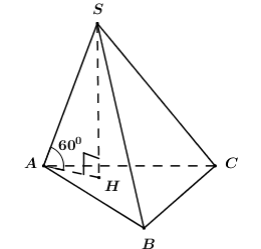
Xét tam giác ABC, giả sử
ta có:
nên tam giác ABC vuông tại B (định lí Pitago)
Gọi H là hình chiếu vuông góc của S lên (ABC) và giả sử SA hợp với đáy góc
HA là hình chiếu của SA lên (ABC)
Vậy
Đáp án cần chọn là: D
Câu 12:
17/07/2024 Xem đáp án
Xem đáp án
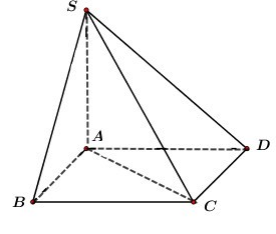
Ta có:
là hình chiếu của SB trên (ABCD)
vuông cân tại A
Đáp án cần chọn là: C
Câu 13:
21/07/2024 Xem đáp án
Xem đáp án
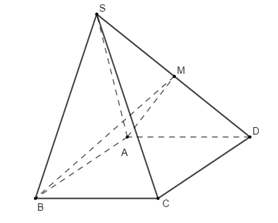
Vì M là trung điểm của SD nên
Mà
Đáp án cần chọn là: C
Câu 14:
23/07/2024 Xem đáp án
Xem đáp án
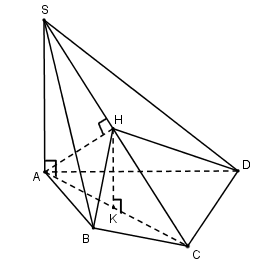
Ta có:
AC là hình chiếu của SC trên (ABCD)
vuông tại A và
Xét tam giác vuông SAC có:
;
Áp dụng hệ thức lượng trong tam giác vuông SAC có:
Trong (SAC) kẻ
Ta có:
Vậy
Đáp án cần chọn là: C
Câu 15:
12/10/2024Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = 2a,
AC = 3a, AD = 4a. Thể tích của khối tứ diện đó là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
* Phương pháp giải:
- Thể tích của một khối tứ diện bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối tứ diện tương ứng
* Lời giải:
Thể tích khối tứ diện ABCD đã cho là:
* Một số lý thuyết liên quan:
Thể tích một số khối chóp đặc biệt
a. Khối tứ diện đều: Là khối chóp có tất cả các cạnh bằng nhau
Tất cả các mặt đều là các tam giác đều. Chân đường cao là trọng tâm của đáy
b. Khối chóp tam giác đều
- Là hình chóp có tất cả các cạnh bên bằng nhau, đáy là tam giác. Chân đường cao là trọng tâm của tam giác đáy.
c. Khối chóp tứ giác đều
- Là hình chóp có tất cả các cạnh bên bằng nhau. Đáy là hình vuông, chân đường cao là tâm của hình vuông.
d. Chóp tam giác có 3 cạnh bên đôi một vuông góc.
- Giả sử 3 cạnh bên có độ dài lần lượt là a, b và c. Khi đó thể tích khối chóp này là:
e. Khối tứ diện gần đều
- Là tứ diện có các cặp cạnh đối bằng nhau.
Xem thêm các bài viết liên quan hay, chi tiết:
50 bài toán về thể tích khối chóp (có đáp án 2024) – Toán 12
TOP 40 câu Trắc nghiệm Khái niệm về khối đa diện (có đáp án 2024) – Toán 12
Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án (Thông hiểu)
Câu 16:
23/07/2024 Xem đáp án
Xem đáp án
Thể tích khối chóp đã cho là:
Đáp án cần chọn là: D
Câu 17:
22/07/2024 Xem đáp án
Xem đáp án
Công thức tính thể tích lăng trụ có diện tích đáy S và chiều cao h là: V = Sh.
Đáp án cần chọn là: D
Câu 18:
22/07/2024 Xem đáp án
Xem đáp án
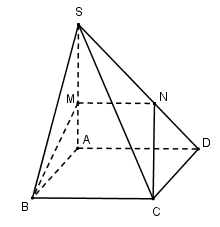
Vì BC // AD nên mặt phẳng (BMC) cắt (SAD) theo đoạn thẳng
Vì
Để mặt phẳng (BMNC) chia hình chóp thành 2 phần có thể tích bằng nhau thì:
do k > 0
Đáp án cần chọn là: B
Câu 19:
23/07/2024Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông
cân tại B, biết . Thể tích khối chóp S.ABC là:
 Xem đáp án
Xem đáp án
Do vuông cân tại B có
Đáp án cần chọn là: A
Câu 20:
23/07/2024 Xem đáp án
Xem đáp án
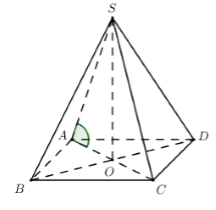
Gọi ta có
Đáp án cần chọn là: B
Câu 21:
13/07/2024 Xem đáp án
Xem đáp án
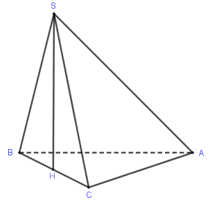
Trong mp (SBC) kẻ
, H là trung điểm BC.
Xét tam giác vuông ABC có
đều cạnh 2a
Đáp án cần chọn là: A
Câu 22:
23/07/2024 Xem đáp án
Xem đáp án
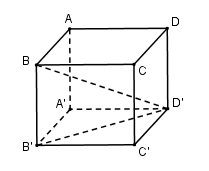
Vì A’B’C’D’ là hình vuông cạnh a nên
vuông tại B'
Vậy
Đáp án cần chọn là: D
Câu 23:
13/07/2024 Xem đáp án
Xem đáp án
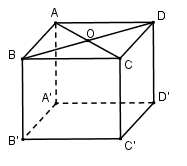
Gọi ta có: OA = 3cm; OB = 4cm.
Xét tam giác vuông OAB có:
Khi đó chu vi đáy bằng
Vậy
Đáp án cần chọn là: C
Câu 24:
22/07/2024Cho đa diện ABCDEF có AD, BE, CF đôi một song song. , diện tích ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:
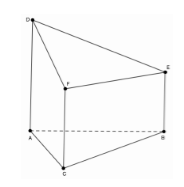
 Xem đáp án
Xem đáp án
Chọn thì đa diện hình lăng trụ đứng ABC.DEF có diện tích đáy , chiều cao
Thể tích
Đáp án cần chọn là: C
Câu 25:
23/07/2024 Xem đáp án
Xem đáp án
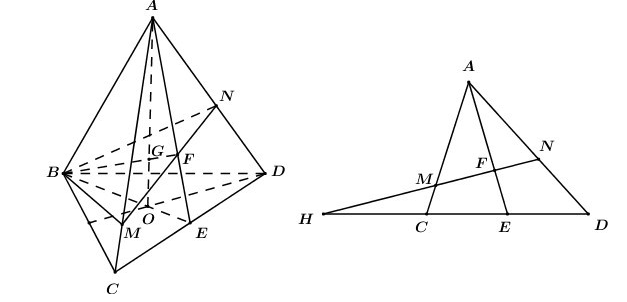
Gọi O là trọng tâm tam giác BCD
Trong (ABC) gọi
Lấy ,
trong (ACD) gọi ,
khi đó ta có mặt phẳng chứ BG cắt AC, AD lần lượt tại M, N chính là (BMN).
Áp dụng định lí Menelaus trong tam giác AOE, cát tuyến BGF:
là trọng tâm tam giác ACD
Trong (ACD) kéo dài MN cắt CD tại H.
Đặt
Áp dụng định lí Menelaus trong tam giác ACE, cát tuyến MHF:
Ta có:
Áp dụng định lí Menelaus trong tam giác AED, cát tuyến MFN:
Khi đó ta có:
Xét hàm số
ta có:
BBT:
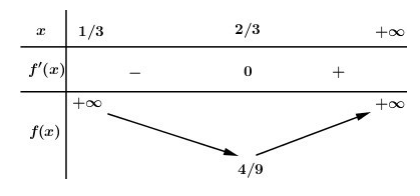
Dựa vào BBT ta thấy
Vậy giá trị nhỏ nhất của tỉ số
Đáp án cần chọn là: B
Có thể bạn quan tâm
- Trắc nghiệm Khái niệm về thể tích của khối đa diện (có đáp án) (447 lượt thi)
- Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng) (493 lượt thi)
- 80 câu trắc nghiệm: Thể tích khối đa diện có đáp án (P1) (389 lượt thi)
- Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án (Nhận biết) (531 lượt thi)
- Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án (Thông hiểu) (408 lượt thi)
- Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án (Vận dụng) (421 lượt thi)
- Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án (Phần 1) (413 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Khái niệm về khối đa diện (có đáp án) (837 lượt thi)
- 70 câu trắc nghiệm Khối đa diện cơ bản (P1) (609 lượt thi)
- 19 câu trắc nghiệm: Khái niệm về khối đa diện có đáp án (581 lượt thi)
- Trắc nghiệm Ôn tập Chương 1 - Khối đa diện (có đáp án) (547 lượt thi)
- Trắc nghiệm Khái niệm về khối đa diện có đáp án (Vận dụng) (508 lượt thi)
- Trắc nghiệm Khối đa diện lồi và khối đa diện đều (có đáp án) (507 lượt thi)
- Trắc nghiệm Khái niệm về khối đa diện có đáp án (Thông hiểu) (456 lượt thi)
- Trắc nghiệm Khái niệm về khối đa diện (nhận biết) (438 lượt thi)
- Trắc nghiệm Ôn tập chương có đáp án (Thông hiểu) (401 lượt thi)
- 80 câu trắc nghiệm Khối đa diện nâng cao (P1) (398 lượt thi)
