Câu hỏi:
12/10/2024 4,153
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = 2a,
AC = 3a, AD = 4a. Thể tích của khối tứ diện đó là:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = 2a,
AC = 3a, AD = 4a. Thể tích của khối tứ diện đó là:
A. 12a3
B. 6a3
C. 8a3
D. 4a3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là: D
* Phương pháp giải:
- Thể tích của một khối tứ diện bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối tứ diện tương ứng
* Lời giải:
Thể tích khối tứ diện ABCD đã cho là:
V=16AB.AC.AD=16.2a.3a.4a=4a3
* Một số lý thuyết liên quan:
Thể tích một số khối chóp đặc biệt
a. Khối tứ diện đều: Là khối chóp có tất cả các cạnh bằng nhau
Tất cả các mặt đều là các tam giác đều. Chân đường cao là trọng tâm của đáy
b. Khối chóp tam giác đều
- Là hình chóp có tất cả các cạnh bên bằng nhau, đáy là tam giác. Chân đường cao là trọng tâm của tam giác đáy.
c. Khối chóp tứ giác đều
- Là hình chóp có tất cả các cạnh bên bằng nhau. Đáy là hình vuông, chân đường cao là tâm của hình vuông.
d. Chóp tam giác có 3 cạnh bên đôi một vuông góc.
- Giả sử 3 cạnh bên có độ dài lần lượt là a, b và c. Khi đó thể tích khối chóp này là: V=16abc
e. Khối tứ diện gần đều
- Là tứ diện có các cặp cạnh đối bằng nhau.
Xem thêm các bài viết liên quan hay, chi tiết:
50 bài toán về thể tích khối chóp (có đáp án 2024) – Toán 12
TOP 40 câu Trắc nghiệm Khái niệm về khối đa diện (có đáp án 2024) – Toán 12
Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án (Thông hiểu)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Nếu khối chóp OABC thỏa mãn OA=a,OB=b,OC=c và OA⊥OB,OB⊥OC,OC⊥OA thì có thể tích là:
Câu 2:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và SA = a. Điểm M thuộc cạnh SA sao cho SMSA=k. Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
Câu 3:
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là tứ giác đều cạnh a, biết rằng BD'. Thể tích của khối lăng trụ?
Câu 4:
Cho khối chóp tam giác S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’. Khi đó:
Câu 5:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên và SA vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng:
Câu 6:
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy một góc . Thể tích của khối chóp đó là:
Câu 7:
Cho đa diện ABCDEF có AD, BE, CF đôi một song song. , diện tích ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:
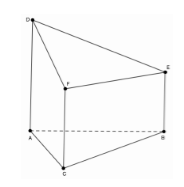
Cho đa diện ABCDEF có AD, BE, CF đôi một song song. , diện tích ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:

Câu 8:
Cho hình chóp đều S.ABCD có cạnh AB = a, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng . Thể tích khối chóp S.ABCD là:
Câu 9:
Cho hình chóp S.ABCD đáy là hình chữ nhật, SA vuông góc với đáy, . Góc giữa SB và đáy bằng . Thể tích khối chóp S.ABC bằng:
Câu 10:
Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là 6cm và 8cm, biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
Câu 11:
Công thức tính thể tích lăng trụ có diện tích đáy S và chiều cao h là:
Câu 12:
Cho hình hộp ABCD.A’B’C’D’ có thể tích bằng V. Gọi M, N, P, Q, E, F lần lượt là tâm các hình bình hành ABCD, A’B’C’D’, ABB’A’, BCC’B’, CDD’C’, DAA’D’. Thể tích khối đa diện có các đỉnh M, P, Q, E, F, N bằng:
Câu 13:
Cho tứ diện ABCD có G là điểm thỏa mãn . Mặt phẳng thay đổi chứ BG và cắt AC, AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số là:
Câu 14:
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại A, SA vuông góc với đáy. Biết , thể tích khối chóp S.ABC bằng:
Câu 15:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông
cân tại B, biết . Thể tích khối chóp S.ABC là:
Cho hình chóp S.ABC có SA vuông góc với đáy. Tam giác ABC vuông
cân tại B, biết . Thể tích khối chóp S.ABC là:


