Câu hỏi:
23/07/2024 295
Cho tứ diện ABCD có G là điểm thỏa mãn . Mặt phẳng thay đổi chứ BG và cắt AC, AD lần lượt tại M và N. Giá trị nhỏ nhất của tỉ số là:
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
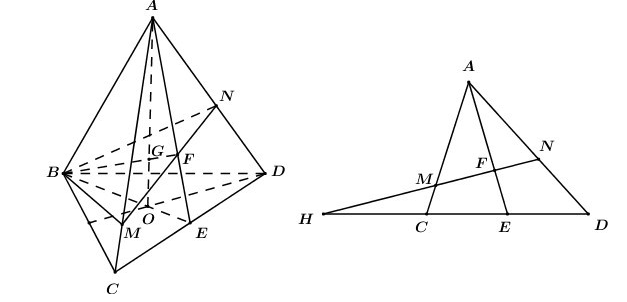
Gọi O là trọng tâm tam giác BCD
Trong (ABC) gọi
Lấy ,
trong (ACD) gọi ,
khi đó ta có mặt phẳng chứ BG cắt AC, AD lần lượt tại M, N chính là (BMN).
Áp dụng định lí Menelaus trong tam giác AOE, cát tuyến BGF:
là trọng tâm tam giác ACD
Trong (ACD) kéo dài MN cắt CD tại H.
Đặt
Áp dụng định lí Menelaus trong tam giác ACE, cát tuyến MHF:
Ta có:
Áp dụng định lí Menelaus trong tam giác AED, cát tuyến MFN:
Khi đó ta có:
Xét hàm số
ta có:
BBT:
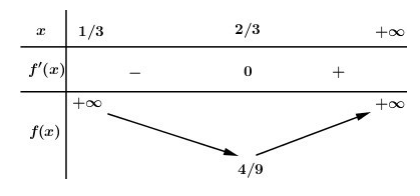
Dựa vào BBT ta thấy
Vậy giá trị nhỏ nhất của tỉ số
Đáp án cần chọn là: B

Gọi O là trọng tâm tam giác BCD
Trong (ABC) gọi
Lấy ,
trong (ACD) gọi ,
khi đó ta có mặt phẳng chứ BG cắt AC, AD lần lượt tại M, N chính là (BMN).
Áp dụng định lí Menelaus trong tam giác AOE, cát tuyến BGF:
là trọng tâm tam giác ACD
Trong (ACD) kéo dài MN cắt CD tại H.
Đặt
Áp dụng định lí Menelaus trong tam giác ACE, cát tuyến MHF:
Ta có:
Áp dụng định lí Menelaus trong tam giác AED, cát tuyến MFN:
Khi đó ta có:
Xét hàm số
ta có:
BBT:

Dựa vào BBT ta thấy
Vậy giá trị nhỏ nhất của tỉ số
Đáp án cần chọn là: B
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = 2a,
AC = 3a, AD = 4a. Thể tích của khối tứ diện đó là:
Cho tứ diện ABCD có AB, AC, AD đôi một vuông góc và AB = 2a,
AC = 3a, AD = 4a. Thể tích của khối tứ diện đó là:
Câu 3:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với mặt phẳng đáy (ABCD) và SA = a. Điểm M thuộc cạnh SA sao cho . Xác định k sao cho mặt phẳng (BMC) chia khối chóp S.ABCD thành hai phần có thể tích bằng nhau.
Câu 4:
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy là tứ giác đều cạnh a, biết rằng . Thể tích của khối lăng trụ?
Câu 5:
Cho khối chóp tam giác S.ABC, trên các cạnh SA, SB, SC lần lượt lấy các điểm A’, B’, C’. Khi đó:
Câu 6:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên và SA vuông góc với mặt phẳng đáy. Thể tích khối chóp S.ABCD bằng:
Câu 7:
Một khối chóp tam giác có cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy một góc . Thể tích của khối chóp đó là:
Câu 8:
Cho hình chóp đều S.ABCD có cạnh AB = a, góc giữa đường thẳng SA và mặt phẳng (ABC) bằng . Thể tích khối chóp S.ABCD là:
Câu 9:
Cho đa diện ABCDEF có AD, BE, CF đôi một song song. , diện tích ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:
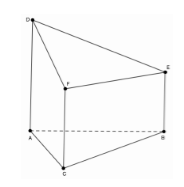
Cho đa diện ABCDEF có AD, BE, CF đôi một song song. , diện tích ta giác ABC bằng 10. Thể tích đa diện ABCDEF bằng:



