100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1)
100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1) (Đề số 4)
-
1390 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
22/07/2024Với giả thiết: tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA, AC và BD. Hãy cho biết trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án D
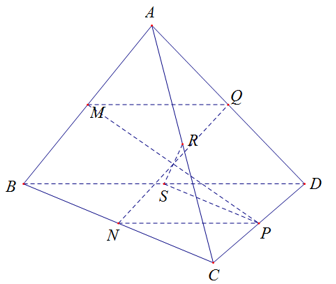
Các phương án đã cho đều sai: Cần sửa thành:
A. MQ, BD, NP đôi một song song
B. Ba đường thẳng MP; NQ; RS đồng quy
C. NQ; SP; RS không đồng phẳng.
Câu 2:
16/07/2024Cho 2 mặt phẳng (P) và (Q) cắt nhau theo giao tuyến . Hai đường thẳng p và q lần lượt nằm trong (P) và (Q). Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Đáp án D
2 đường thẳng p và q có thể song song, chéo nhau, hoặc cắt nhau
Câu 3:
18/07/2024Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
 Xem đáp án
Xem đáp án
Đáp án D
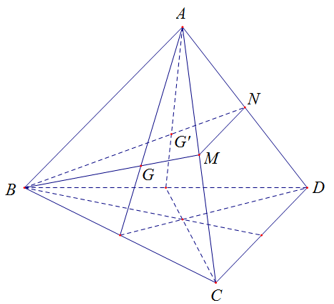
Trong(ABC), ta có: BG cắt AC tại M
Trong (ABD), ta có: BG’ cắt AD tại N
(BGG’)(ACD) = MN
Thiết diện cần tìm là (BMN)
Xét tam giác BMN có:
MN = CD = ( MN là đường trung bình của tam giác ACD)
BM = BN = (BM, BN lần lượt là đường trung tuyến - đường cao của tam giác đều ABC, ABD có độ dài cạnh bằng a)
Áp dụng công thức hê- rông :
Trong đó: là nửa chu vi của tam giác
Câu 4:
18/07/2024Cho hai hình bình hành ABCD và ABEF nằm trong 2 mặt phẳng phân biệt. Kết quả nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án D
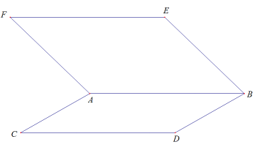
Câu 5:
16/07/2024Cho hình chóp S.ABCD. Gọi A’, B’, C’, D’ lần lượt là trung điểm của các cạnh SA, SB, SC, SD. Một mặt phẳng (P) thay đổi qua A’ và song song với AC luôn đi qua một đường thẳng cố định là:
 Xem đáp án
Xem đáp án
Đáp án C
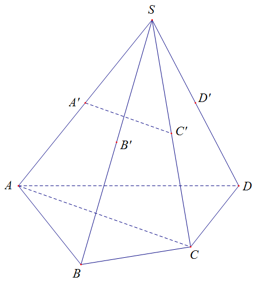
Mặt phẳng (P) đi qua A’ và song song AC
Trong mặt phẳng (SAC), ta có A’C’//AC (A’C’ là đường trung bình tam giác SAC)
(P) đi qua A’C’ cố định
Câu 6:
19/07/2024Với giả thiết: hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Ta có:
 Xem đáp án
Xem đáp án
Đáp án D

Gọi M là điểm bất kì trên cạnh SA
Trong (SAB), kẻ Mx // SB, Mx cắt AB tại N
Trong (ABCD), kẻ Ny // AC, Ny cắt BC tại E
Ny cắt BD tại J
Trong (SBC), kẻ Ez // SB, Ez cắt SC tại F
Trong (SBD), kẻ Jt // SB, Jt cắt SD tại I
+ Theo cách dựng ta có: IJ // SB
Mà nên IJ // (SAB)
Câu 7:
26/10/2024Cho hai mặt phẳng (P) và (Q) song song với nhau. Mệnh đề nào sau đây sai:
 Xem đáp án
Xem đáp án
Đáp án đúng: C
* Lời giải:
2 đường thẳng có thể chéo nhau
* Phương pháp giải:
- nắm lại lý thuyết và tính chất về 2 mặt phẳng song song với nhau
* Lý thuyết cần nắm thêm về đường thẳng và mặt phẳng trong không gian:
Mặt phẳng
- Biểu diễn một mặt phẳng: Người ta thường biểu diễn mặt phẳng bằng một hình bình hành.
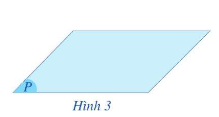
- Để kí hiệu mặt phẳng ta dùng chữ cái in hoa đặt trong dấu ngoặc ( ).
Điểm thuộc mặt phẳng
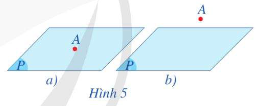
- Điểm A thuộc mặt phẳng (P), ta kí hiệu
- Điểm A không thuộc mặt phẳng (P) ta kí hiệu .
Hình biểu diễn của một hình trong không gian
a, Khái niệm: Hình được vẽ trong mặt phẳng để giúp ta hình dung được về một hình trong không gian gọi là hình biểu diễn của hình không gian đó.
b, Quy tắc vẽ hình biểu diễn của một hình trong không gian
- Đường thẳng được biểu diễn bởi đường thẳng, đoạn thẳng được biểu diễn bởi đoạn thẳng.
- Hai đường thẳng song song (hoặc cắt nhau) được biểu diễn bởi 2 đường thẳng song song (hoặc cắt nhau).
- Hình biểu diễn giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.
- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn để biểu diễn cho đường bị che khuất
Các tính chất thừa nhận của hình học không gian
- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
- Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.
- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu hoặc .
- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu .
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.
Hai mặt phẳng song song
- Hai mặt phẳng (α) và (β) được gọi là song song với nhau nếu chúng không có điểm chung, kí hiệu (α) // (β) hay (β) // (α).
Nhận xét: Nếu hai mặt phẳng (α) và (β) song song với nhau và đường thẳng d nằm trong (α) thì d và (β) không có điểm chung, tức là d song song với (β). Như vậy, nếu một đường thẳng nằm trong một trong hai mặt phẳng song song thì đường thẳng đó song song với mặt phẳng còn lại.
Điều kiện và tính chất của hai mặt phẳng song song
• Điều kiện để hai mặt phẳng song song: Nếu mặt phẳng (α) chứa hai đường thẳng cắt nhau và hai đường thẳng này song song với mặt phẳng (β) thì (α) và (β) song song với nhau.
• Tính chất của hai mặt phẳng song song:
-Qua một điểm nằm ngoài một mặt phẳng cho trước có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.
- Cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song với nhau.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Đường thẳng và mặt phẳng trong không gian – Toán 11 Kết nối tri thức
Toán 11 Bài 10 SGK (Kết nối tri thức): Đường thẳng và mặt phẳng trong không gian
Trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án 2023) – Toán 11
Câu 8:
16/07/2024Chọn câu trả lời đúng:Nếu ba đường thẳng không cùng nằm trong một mặt phẳng và đôi một cắt nhau thì ba đường thẳng đó?
 Xem đáp án
Xem đáp án
Đáp án A
Câu 11:
20/07/2024Cho mặt phẳng (P) và đường thẳng d(P). Mệnh đề nào sau đây đúng:
 Xem đáp án
Xem đáp án
Đáp án C
Câu 12:
16/07/2024Cho 4 điểm không đồng phẳng A, B, C, D.Gọi M là trung điểm AD. Khẳng định nào sao đây là đúng:
 Xem đáp án
Xem đáp án
Đáp án D
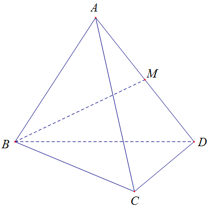
Câu 13:
16/07/2024Cho 4 điểm không đồng phẳng A, B, C, D. Khi đó giao tuyến của mp (ABC) và mp (BCD) là:
 Xem đáp án
Xem đáp án
Đáp án B
Xét hai mp( ABC) và (BCD) có:
B chung
C chung
Do đó, giao tuyến của 2 mp trên là đường thẳng BC.
Câu 14:
22/09/2024Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (MBC) và mp (NDA) là:
 Xem đáp án
Xem đáp án
Đáp án D
*Lời giải

MADM(NDA)
NBC nên N( MBC)
Xét (NDA) và (MBC) có
M là điểm chung
N là điểm chung
Giao tuyến của 2 mặt phẳng là MN
*Lý thuyết liên quan
- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
- Nếu có một đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.
- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu hoặc .
- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu .
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.
Xem thêm các bài toán hay, chi tiết khác
Lý thuyết Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian - Kết nối tri thức
Giải Toán 11 Bài 10: Đường thẳng và mặt phẳng trong không gian
Câu 15:
16/07/2024Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (AMN) và mp (BCD) là:
 Xem đáp án
Xem đáp án
Đáp án A
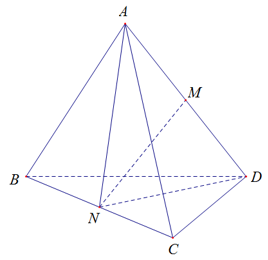
DAMD(AMN)
NBCN(BCD)
Xét (AMN) và (BCD) có:
D là điểm chung
N là điểm chung
Giao tuyến của 2 mặt phẳng là ND
Câu 16:
15/11/2024Trong các điều kiện sau, điều kiện nào kết luận đường thẳng a song song với mp (P)
 Xem đáp án
Xem đáp án
Đáp án đúng là : D
- Điều kiện a⊂Q và (Q) // (P),kết luận đường thẳng a song song với mp (P).
- Các trường hợp A, B, C đều có khả năng a nằm trên mặt phẳng (P).
→ D đúng.A,B,C sai.
* Vị trí tương đối của đường thẳng và mặt phẳng.
Cho đường thẳng d và mặt phẳng (α). Tùy theo số điểm chung của d và (α), ta có ba trường hợp sau:
- d và (α) không có điểm chung. Khi đó ta nói d song song với (α) hay (α) song song với d và kí hiệu là d // (α) hay (α) // d.
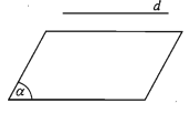
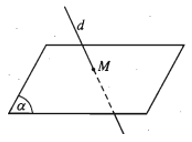
- d và (α) chỉ có một điểm chung duy nhất M. Khi đó ta nói d và (α) cắt nhau tại điểm M và kí hiệu .
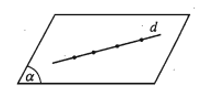
- d và (α) có từ hai điểm chung trở lên. Khi đó, d nằm trong (α) hay (α) chứa d và kí hiệu .
II. Tính chất
- Định lí. Nếu đường thẳng d không nằm trong mặt phẳng (α) và d song song với đường thẳng d’ nằm trong (α) thì d song song với (α).
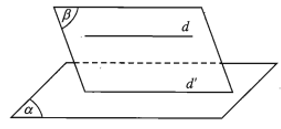
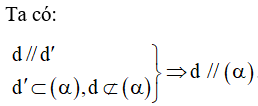
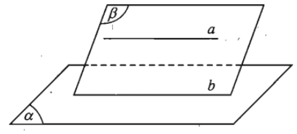
- Định lí. Cho đường thẳng a song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa a và cắt (α) theo giao tuyến b thì b song song với a.
- Hệ quả. Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
- Định lí. Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia.
Xem thêm các bài viết liên quan,chi tiết khác:
Lý thuyết Toán 11 Bài 3: Đường thẳng và mặt phẳng song song
Mục lục Giải Toán 11 Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song
Câu 17:
23/07/2024Cho hai đường thẳng phân biệt a và b cùng song song với mp (P). Có bao nhiêu vị trí tương đối của a và b?
 Xem đáp án
Xem đáp án
Đáp án C
Có 3 vị trí: song song, chéo nhau, cắt nhau. ( chú ý 2 đường thẳng a và b là 2 đường thẳng phân biệt nên không thể trùng nhau)
Câu 18:
29/10/2024Cho hai đường thẳng chéo nhau a, b. Chọn khẳng định sai?
 Xem đáp án
Xem đáp án
Đáp án đúng: A
*Lời giải
Có vô số mặt phẳng song song với a và b
*Phương pháp giải
- nắm kỹ kiến thức về đường thẳng và mặt phẳng trong không gian để chọn đáp án cho đúng
*Lý thuyết cần nắm và dạng bài toán về đường thẳng và mặt phẳng trong không gian:
- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
- Nếu có một đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.
- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu d⊂(P) hoặc .
- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu .
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hìnd=(P)∩(Q)h học phẳng đều đúng.
Cách xác định mặt phẳng
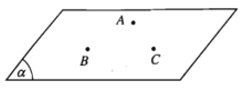
1) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.
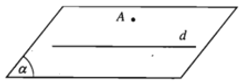
2) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.
Cho đường thẳng d và điểm A không thuộc d. Khi đó điểm A và đường thẳng d xác định một mặt phẳng, kí hiệu là mp(A, d) hay (A, d) hoặc mp(d, A) hay (d, A).
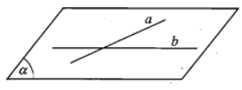
3) Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
Cho hai đường thẳng cắt nhau a và b. Khi đó hai đường thẳng a và b xác định một mặt phẳng và kí hiệu là mp(a, b) hay (a, b) hoặc mp(b, a) hay (b, a).
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Đường thẳng và mặt phẳng trong không gian – Toán 11 Kết nối tri thức
Toán 11 Bài 10 SGK (Kết nối tri thức): Đường thẳng và mặt phẳng trong không gian
TOP 40 câu Trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án) – Toán 11
Câu 19:
16/07/2024Cho hai đường thẳng phân biệt a, b. Trong các điều kiện sau, điều kiện nào đủ để kết luận được hai đường thẳng a và b song song với nhau
 Xem đáp án
Xem đáp án
Đáp án B
Câu 20:
16/07/2024Cho hình tứ diện ABCD và các điểm M, N, M’, N’ như hình vẽ ( M khác M’, N khác N’). Hai đường thẳng MN và M’N’
 Xem đáp án
Xem đáp án
Đáp án A
Câu 23:
21/07/2024Xét các mệnh đề:
(I) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua ba điểm.
(II) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua một điểm và chứa 1 đường thẳng.
(III) Mặt phẳng hoàn toàn được xác định khi biết nó chứa hai đường thẳng cắt nhau.
Số khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án B
Mệnh đề sai:
+ Mệnh đề (I) sai vì nếu 3 điểm đó có 2 điểm trùng nhau thì ta vẫn chưa thể xác định được mặt phẳng .
+ (II) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua một điểm và chứa 1 đường thẳng không đi qua điểm đó.
Câu 24:
23/07/2024Cho hai đường thẳng cắt nhau Ox, Oy và 2 điểm A, B không nằm trong mặt phẳng (Ox, Oy). Biết rằng đường thẳng AB và mặt phẳng (Ox, Oy) có điểm chung I. Một mặt phẳng thay đổi luôn chứa AB và cắt Ox tại M, cắt Oy tại N. Ta chứng minh được rằng đường thẳng MN luôn đi qua một điểm cố định khi thay đổi. Điểm đó là
 Xem đáp án
Xem đáp án
Đáp án D

AB và mặt phẳng (Ox, Oy) luôn có điểm chung I
chứa AB
I luôn nằm trên giao tuyến của và (Ox, Oy) (1)
Ta lại có: thay đổi cắt Ox tại M, Oy tại N
Xét và (Ox, Oy) có M và N là điểm chung
MN là giao tuyến của 2 mặt phẳng (2)
(1);(2): M, N, I thẳng hàng
MN luôn đi qua I cố định
Câu 25:
16/07/2024Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi M, N lần lượt là trung điểm của SA, SB. Gọi P là giao điểm của SC và (AND). AN cắt DP tại I. SABI là hình gì?
 Xem đáp án
Xem đáp án
Đáp án A
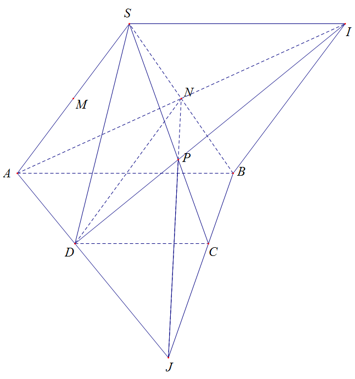
Xét (ABCD) có:
JBCJ(SBC)
Xét (SBC), Kẻ JN cắt SC tại P
Xét (SAB) và (SCD) có :
S là điểm chung
AB // CD
Giao tuyến của 2 mp này là đường thẳng d qua S song song với AB (1)
Lại có: I là giao điểm của 2 đường thẳng AN và DP nên I cũng thuộc giao tuyến của 2 mp ( SAB) và ( SCD) (2) '
Từ (1) và (2) suy ra: điểm I thuộc đường thẳng d hay đường thẳng d chính là đường thẳng SI
Suy ra: SI // AB
ASIB là hình thang có: SN = NB ( N là trung điểm SB)
Áp dụng định lí Ta let vào tam giác ANB có AB// SI có:
nên AN = NI hay N là trung điểm của AI
ASIB là hình bình hành (hình thang có 2 đường chéo cắt nhau tại trung điểm mỗi đường).
Bài thi liên quan
-
100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1) (Đề số 1)
-
25 câu hỏi
-
50 phút
-
-
100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1) (Đề số 2)
-
25 câu hỏi
-
50 phút
-
-
100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1) (Đề số 3)
-
25 câu hỏi
-
50 phút
-
Có thể bạn quan tâm
- Trắc nghiệm Ôn chương 2 - hình học (có đáp án) (533 lượt thi)
- 100 câu trắc nghiệm Đường thẳng - Mặt phẳng trong không gian (P1) (1389 lượt thi)
- 100 câu trắc nghiệm Đường thẳng, Mặt phẳng trong không gian nâng cao (phần 1) (1223 lượt thi)
- Trắc nghiệm Ôn tập Toán 11 Chương 2 Hình học có đáp án (310 lượt thi)
Các bài thi hot trong chương
- Trắc nghiệm Đường thẳng và mặt phẳng song song (có đáp án) (1144 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song (có đáp án) (992 lượt thi)
- Trắc nghiệm Hai mặt phẳng song song (có đáp án) (748 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án) (562 lượt thi)
- Trắc nghiệm Phép chiếu song song. Hình biểu diễn của một hình không gian (có đáp án) (545 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (516 lượt thi)
- Trắc nghiệm Hai đường thẳng chéo nhau và hai đường thẳng song song có đáp án (Vận dụng) (415 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (408 lượt thi)
- Trắc nghiệm Đường thẳng và mặt phẳng song song có đáp án (Nhận biết) (407 lượt thi)
- Trắc nghiệm Đại cương về đường thẳng và mặt phẳng có đáp án (Vận dụng) (407 lượt thi)



