Trắc nghiệm Ôn tập Toán 11 Chương 2 Hình học có đáp án
-
282 lượt thi
-
24 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
18/07/2024Cho hai đường thẳng a và b chéo nhau. Có bao nhiêu mặt phẳng chứa a và song song với b?
Xem đáp án
Cho hai đường thẳng chéo nhau, có duy nhất một mặt phẳng qua đường thẳng này và song song với đường thẳng kia.
Đáp án cần chọn là: D
Câu 2:
14/11/2024Các yếu tố nào sau đây xác định một mặt phẳng duy nhất?
Xem đáp án
Đáp án đúng là : C
Lời giải
- Các yếu tố ,xác định một mặt phẳng duy nhất là hai đường thẳng cắt nhau.
- A sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì sẽ có vô số mặt phẳng chứa 3 điểm thẳng hàng đã cho.
- B sai. Trong trường hợp điểm thuộc đường thẳng đã cho, khi đó ra chỉ có 1 đường thẳng, có vô số mặt phẳng đi qua đường thẳng đó.
- D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm đó hoặc trong trường hợp 4 điểm không đồng phẳng thì sẽ không tạo được mặt phẳng nào đi qua cả 4 điểm.
→ C đúng.A,B,D sai.
*Phương pháp giải:
* Mặt phẳng
Hình ảnh mặt phẳng trong thực tiễn
- Biểu diễn một mặt phẳng: Người ta thường biểu diễn mặt phẳng bằng một hình bình hành.
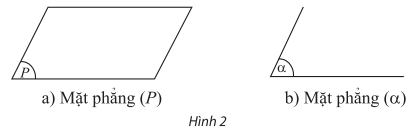
- Để kí hiệu mặt phẳng ta dùng chữ cái in hoa đặt trong dấu ngoặc ( ). Mặt phẳng (P) còn được viết là mp(P) hay (P).
* Điểm thuộc mặt phẳng
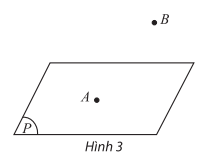
- Điểm A thuộc mặt phẳng (P) thì ta nói A nằm trên (P) hay (P) chứa A, ta kí hiệu
- Điểm B không thuộc mặt phẳng (P) thì ta nói B nằm ngoài (P) hay (P) không chứa B, ta kí hiệu .
* Biểu diễn các hình lên một mặt phẳng
- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.
- Hình biểu diễn của hai đường thẳng song song là 2 đường thẳng song song, của 2 đường thẳng cắt nhau là 2 đường thẳng cắt nhau.
- Hình biểu diễn giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.
- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn để biểu diễn cho đường bị che khuất.
*Lý thuyết:
Các tính chất thừa nhận của hình học không gian
- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.
- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
- Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.
- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu hoặc .
- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu .
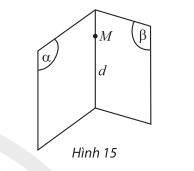
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.
3. Cách xác định mặt phẳng
- Một mặt phẳng hoàn toàn được xác định khi biết nó chứa 3 điểm không thẳng hàng.
- Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua một đường thẳng và một điểm không thuộc đường thẳng đó.
- Một mặt phẳng được hoàn toàn xác định nếu biết nó chứa hai đường thẳng cắt nhau.
Xem thêm các bài viết liên quan,chi tiết khác:
Lý thuyết Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian - Chân trời sáng tạo
Giải SBT Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian
Câu 3:
20/07/2024Tìm khẳng định đúng trong các khẳng định sau.
Xem đáp án
A. Đúng.
B. Sai vì hai mặt phẳng có thể trùng nhau.
C. Sai vì ba giao tuyến có thể song song hoặc trùng nhau.
D. Sai hai đường thẳng đó có thể trùng nhau hoặc chéo nhau hoặc cắt nhau.
Đáp án cần chọn là: A
Câu 4:
23/07/2024Trong các mệnh đề sau, mệnh đề nào sai?
Xem đáp án
Mệnh đề “Hai đường thẳng không có điểm chung thì song song với nhau” chỉ đúng trong mặt phẳng, còn trong không gian thì hai đường thẳng không có điểm chung thì hoặc song song với nhau hoặc chéo nhau.
Đáp án cần chọn là: A
Câu 5:
23/07/2024Hình chóp lục giác có bao nhiêu mặt bên?
Xem đáp án
Quan sát hình vẽ ta thấy hình chóp lục giác đều có 6 mặt bên.
Đáp án cần chọn là: B
Câu 6:
18/07/2024Trong không gian cho bốn điểm không đồng phẳng. Có thể xác định được bao nhiêu mặt phẳng phân biệt từ các điểm đã cho?
Xem đáp án
Số mặt phẳng tạo thành là số cách chọn 3 trong 4 điểm đã cho.
Vậy có 4 mặt phẳng.
Đáp án cần chọn là: B
Câu 7:
18/07/2024Tìm khẳng định sai trong các khẳng định sau đây?
Xem đáp án
Nếu mặt phẳng (P) có chứa hai đường thẳng phân biệt và hai đường thẳng đó cùng song song với mặt phẳng (Q) thì mặt phẳng (P) song song với mặt phẳng (Q) là mệnh đề sai khi hai đường thẳng đó song song với nhau (hai đường thẳng đó phải cắt nhau mới đúng).
Đáp án cần chọn là: D
Câu 8:
19/07/2024Lăng trụ tam giác có bao nhiêu mặt?
Xem đáp án
Lăng trụ tam giác có 5 mặt gồm 3 mặt bên và 2 mặt đáy.
Đáp án cần chọn là: D
Câu 11:
20/07/2024Cho bốn mệnh đề sau:
(I) Nếu hai mặt phẳng (α) và (β) song song với nhau thì mọi đường thẳng nằm trong mặt phẳng (α) đều song song với (β).
(II) Hai đường thẳng nằm trên hai mặt phẳng song song thì song song với nhau.
(III) Trong không gian hai đường thẳng không có điểm chung thì chéo nhau.
(IV) Có thể tìm được hai đường thẳng song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước.
Trong các mệnh đề trên có bao nhiêu mệnh đề sai?
Xem đáp án
Có 3 mệnh đề sai là (II), (III), (IV).
(II) sai vì hai đường thẳng nằm trên hai mặt phẳng song song thì có thể song song hoặc chéo nhau.
(III) sai vì hai đường thẳng không có điểm chung thì có thể chéo nhau hoặc song song với nhau.
(IV) sai vì nếu tồn tại hai đường song song mà mỗi đường thẳng cắt đồng thời hai đường thẳng chéo nhau cho trước thì cả bốn đường đó sẽ đồng phẳng (mâu thuẫn với dữ kiện hai đường thẳng ban đầu chéo nhau).
Đáp án cần chọn là: D
Câu 17:
23/07/2024Hai mặt phẳng song song có bao nhiêu mặt phẳng đối xứng?
Xem đáp án
Do mặt phẳng không có bề dày và không có giới hạn nên hai mặt phẳng song song có một mặt phẳng đối xứng là mặt phẳng nằm cách đều hai mặt phẳng song song đó và có vô số mặt phẳng đối xứng khác là các mặt phẳng vuông góc với hai mặt phẳng đã cho.
Đáp án cần chọn là: D
