Các yếu tố nào sau đây xác định một mặt phẳng duy nhất? 

Đáp án đúng là : C

Lời giải

- Các yếu tố ,xác định một mặt phẳng duy nhất là hai đường thẳng cắt nhau. 

- A sai. Trong trường hợp 3 điểm phân biệt thẳng hàng thì sẽ có vô số mặt phẳng chứa 3 điểm thẳng hàng đã cho.

- B sai. Trong trường hợp điểm thuộc đường thẳng đã cho, khi đó ra chỉ có 1 đường thẳng, có vô số mặt phẳng đi qua đường thẳng đó.

- D sai. Trong trường hợp 4 điểm phân biệt thẳng hàng thì có vô số mặt phẳng đi qua 4 điểm đó hoặc trong trường hợp 4 điểm không đồng phẳng thì sẽ không tạo được mặt phẳng nào đi qua cả 4 điểm.

→ C đúng.A,B,D sai.

*Phương pháp giải:

* Mặt phẳng

Hình ảnh mặt phẳng trong thực tiễn

- Biểu diễn một mặt phẳng: Người ta thường biểu diễn mặt phẳng bằng một hình bình hành.

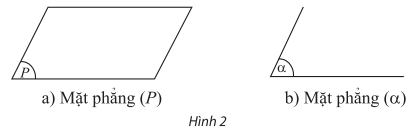
- Để kí hiệu mặt phẳng ta dùng chữ cái in hoa đặt trong dấu ngoặc ( ). Mặt phẳng (P) còn được viết là mp(P) hay (P).

* Điểm thuộc mặt phẳng

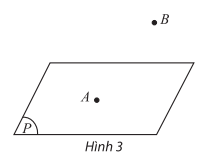
- Điểm A thuộc mặt phẳng (P) thì ta nói A nằm trên (P) hay (P) chứa A, ta kí hiệu $A\in (P)$

- Điểm B không thuộc mặt phẳng (P) thì ta nói B nằm ngoài (P) hay (P) không chứa B, ta kí hiệu $B\notin (P)$.

* Biểu diễn các hình lên một mặt phẳng

- Hình biểu diễn của đường thẳng là đường thẳng, của đoạn thẳng là đoạn thẳng.

- Hình biểu diễn của hai đường thẳng song song là 2 đường thẳng song song, của 2 đường thẳng cắt nhau là 2 đường thẳng cắt nhau.

- Hình biểu diễn giữ nguyên quan hệ liên thuộc giữa điểm và đường thẳng.

- Dùng nét liền để biểu diễn cho đường nhìn thấy và nét đứt đoạn để biểu diễn cho đường bị che khuất.

*Lý thuyết:

Các tính chất thừa nhận của hình học không gian

- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.

- Nếu một đường thẳng đi qua hai điểm phân biệt của một mặt phẳng thì mọi điểm của đường thẳng đều nằm trong mặt phẳng đó.

- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.

- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu $d\subset (P)$ hoặc $(P)\supset d$.

- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu $d=(\alpha )\cap (\beta )$.

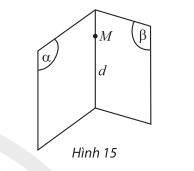
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.

3. Cách xác định mặt phẳng

- Một mặt phẳng hoàn toàn được xác định khi biết nó chứa 3 điểm không thẳng hàng.

- Một mặt phẳng được hoàn toàn xác định khi biết nó đi qua một đường thẳng và một điểm không thuộc đường thẳng đó.

- Một mặt phẳng được hoàn toàn xác định nếu biết nó chứa hai đường thẳng cắt nhau.

Xem thêm các bài viết liên quan,chi tiết khác:

Lý thuyết Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian - Chân trời sáng tạo

Giải SBT Toán 11 Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian