Câu hỏi:
29/10/2024 2,366Cho hai đường thẳng chéo nhau a, b. Chọn khẳng định sai?
A. Có duy nhất một mặt phẳng song song với a và b
B. Có duy nhất một mặt phẳng chứa a và song song với b
C. Có vô số đường thẳng song song với a và cắt b
D. Có duy nhất một mặt phẳng chứa b và song song với a
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: A
*Lời giải
Có vô số mặt phẳng song song với a và b
*Phương pháp giải
- nắm kỹ kiến thức về đường thẳng và mặt phẳng trong không gian để chọn đáp án cho đúng
*Lý thuyết cần nắm và dạng bài toán về đường thẳng và mặt phẳng trong không gian:
- Có một và chỉ một đường thẳng đi qua hai điểm phân biệt.
- Có một và chỉ một mặt phẳng đi qua 3 điểm không thẳng hàng.
- Tồn tại 4 điểm không cùng thuộc một mặt phẳng.
- Nếu có một đường thẳng có 2 điểm phân biệt thuộc một mặt phẳng thì tất cả các điểm của đường thẳng đều thuộc mặt phẳng đó.
- Nếu mọi điểm của đường thẳng d đều thuộc mặt phẳng (P) thì ta nói d nằm trong (P) hoặc (P) chứa d. Kí hiệu hoặc .
- Nếu hai mặt phẳng phân biệt có điểm chung thì các điểm chung của hai mặt phẳng là một đường thẳng đi qua điểm chung đó. Đường thẳng đó được gọi là giao tuyến, kí hiệu .
- Trên mỗi mặt phẳng, tất cả các kết quả đã biết trong hình học phẳng đều đúng.
Cách xác định mặt phẳng
1) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.
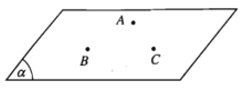
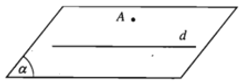
2) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.
Cho đường thẳng d và điểm A không thuộc d. Khi đó điểm A và đường thẳng d xác định một mặt phẳng, kí hiệu là mp(A, d) hay (A, d) hoặc mp(d, A) hay (d, A).
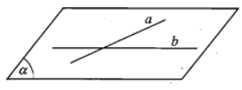
3) Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.
Cho hai đường thẳng cắt nhau a và b. Khi đó hai đường thẳng a và b xác định một mặt phẳng và kí hiệu là mp(a, b) hay (a, b) hoặc mp(b, a) hay (b, a).
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Đường thẳng và mặt phẳng trong không gian – Toán 11 Kết nối tri thức
Toán 11 Bài 10 SGK (Kết nối tri thức): Đường thẳng và mặt phẳng trong không gian
TOP 40 câu Trắc nghiệm Đại cương về đường thẳng và mặt phẳng (có đáp án) – Toán 11
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho 4 điểm không đồng phẳng A, B, C, D. Gọi M, N lần lượt là trung điểm của AD và BC. Khi đó giao tuyến của mp (MBC) và mp (NDA) là:
Câu 2:
Xét các mệnh đề:
(I) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua ba điểm.
(II) Mặt phẳng hoàn toàn được xác định khi biết nó đi qua một điểm và chứa 1 đường thẳng.
(III) Mặt phẳng hoàn toàn được xác định khi biết nó chứa hai đường thẳng cắt nhau.
Số khẳng định đúng là
Câu 3:
Cho hai mặt phẳng (P) và (Q) song song với nhau. Mệnh đề nào sau đây sai:
Câu 4:
Trong các điều kiện sau, điều kiện nào kết luận đường thẳng a song song với mp (P)
Câu 5:
Cho hai đường thẳng phân biệt a và b cùng song song với mp (P). Có bao nhiêu vị trí tương đối của a và b?
Câu 6:
Cho 4 điểm không đồng phẳng A, B, C, D. Khi đó giao tuyến của mp (ABC) và mp (BCD) là:
Câu 9:
Cho hai hình bình hành ABCD và ABEF nằm trong 2 mặt phẳng phân biệt. Kết quả nào sau đây là đúng?
Câu 10:
Cho hai đường thẳng cắt nhau Ox, Oy và 2 điểm A, B không nằm trong mặt phẳng (Ox, Oy). Biết rằng đường thẳng AB và mặt phẳng (Ox, Oy) có điểm chung I. Một mặt phẳng thay đổi luôn chứa AB và cắt Ox tại M, cắt Oy tại N. Ta chứng minh được rằng đường thẳng MN luôn đi qua một điểm cố định khi thay đổi. Điểm đó là
Câu 12:
Cho tứ diện đều ABCD có cạnh a. Gọi G, G’ lần lượt là trọng tâm của tam giác ABC và ABD. Diện tích của thiết diện của hình tứ diện khi cắt bởi mặt phẳng (BGG’) là:
Câu 13:
Cho 2 mặt phẳng (P) và (Q) cắt nhau theo giao tuyến . Hai đường thẳng p và q lần lượt nằm trong (P) và (Q). Trong các mệnh đề sau, mệnh đề nào đúng?
Câu 14:
Với giả thiết: tứ diện ABCD. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DA, AC và BD. Hãy cho biết trong các mệnh đề sau, mệnh đề nào đúng?
Câu 15:
Với giả thiết: hình chóp S.ABCD có đáy là một hình bình hành. Một mặt phẳng (P) đồng thời song song với AC và SB lần lượt cắt các đoạn thẳng SA, AB, BC, SC, SD và BD tại M, N, E, F, I, J. Ta có:


