Tính góc C của tam giác ABC biết a ≠ b và a(a² – c²) = b(b² – c²).

Đáp án đúng: B

*Phương pháp giải:

- Biến đổi a(a² – c²) = b(b² – c²): 

+ chuyển về để vế bên phải là số 0. khai triển ra và triệt tiêu dần để thu gọn lại. 

+ Áp dụng định lý cosin trong tam giác để tìm ra số đo góc C

*Lời giải:

Ta có: a(a² – c²) = b(b² – c²)

⇔ a³ – b³ – c²(a – b) = 0

⇔ (a – b)(a² + ab + b²) – c²(a – b) = 0

⇔ (a – b)(a² + ab + b² – c²) = 0

⇔ a² + ab + b² – c² = 0 (Vì a ≠ b nên a – b ≠ 0)

⇔ a² + b² – c² = – ab

Ta có $\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{{ - ab}}{{2ab}}$$= - \frac{1}{2}$.

Do đó: $\widehat C$ = 120°.

* Lý thuyết và các dạng bài toán về hệ thức lượng trong tam giác:

 Định lí Côsin 

Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

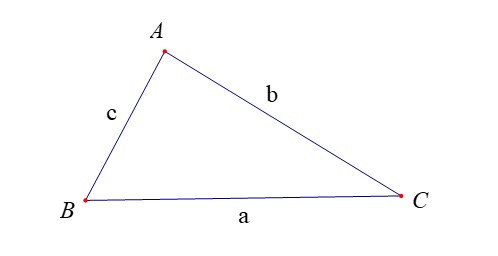
Trong tam giác ABC:

a2 = b2 + c2 – 2bc.cosA.

b2 = c2 + a2 – 2ca.cosB.

c2 = a2 + b2 – 2ab.cosC.

Định lí sin

Trong tam giác ABC: $\frac{\mathrm{a}}{\mathrm{sinA}}=\frac{\mathrm{b}}{\mathrm{sinB}}=\frac{\mathrm{c}}{\mathrm{sinC}}=2\mathrm{R}$.

Công thức tính diện tích tam giác

Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

Ta có các công thức tính diện tích tam giác ABC sau:

+) S = pr =$\frac{\sqrt{3}}{2}$ $\frac{(a+b+c)r}{2}$

+) S = $\frac{1}{2}$bc sin A = $\frac{1}{2}$ca sin B = $\frac{1}{2}$ab sin C.

+) S = $\frac{abc}{4R}$

 

+) Công thức Heron: S = $\sqrt{p(p-a)(p-b)(p-c)}$.

Xem thêm các bài viết liên quan hay, chi tiết:

Lý thuyết Hệ thức lượng trong tam giác – Toán 10 Kết nối tri thức 

Sách bài tập Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác 

Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án