Câu hỏi:
15/11/2024 15,789
Tìm tọa độ tâm đường tròn đi qua 3 điểm .
A. .
B. .
C. .
D. .
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Lời giải
Gọi I(a,b)
Do I là tâm đường tròn đi qua ba điểm nên
Vậy tâm I(0;0).
*Phương pháp giải:
- Gọi phương trình đường tròn là .
- Thay tọa độ các điểm vào phương trình tìm và suy ra tọa độ tâm.
*Lý thuyết:
Trong mặt phẳng Oxy, cho đường tròn (C) tâm I(a; b), bán kính R.
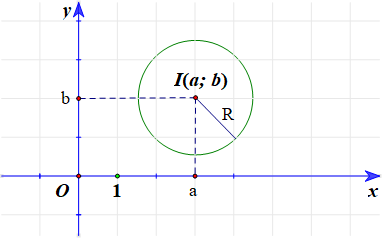Phương trình (x – a)2 + (y – b)2 = R2 được gọi là phương trình đường tròn tâm I(a; b), bán kính R.
Nhận xét: Ta có (x – a)2 + (y – b)2 = R2
⇔ x2 + y2 – 2ax – 2by + (a2 + b2 – R2) = 0.
Vậy phương trình đường tròn (x – a)2 + (y – b)2 = R2 có thể được viết dưới dạng x2 + y2 – 2ax – 2by + c = 0, trong đó c = a2 + b2 – R2.
Ngược lại, phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình của đường tròn (C) khi và chỉ khi a2 + b2 – c > 0. Khi đó đường tròn (C) có tâm I(a; b) và bán kính .
Xem thêm
Lý thuyết Đường tròn trong mặt phẳng tọa độ – Toán 10 Chân trời sáng tạoCÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Phương trình nào sau đây không phải là phương trình đường tròn ?
Câu 3:
Đường tròn tiếp xúc đường thẳng nào trong các đường thẳng dưới đây?
Câu 6:
Một đường tròn có tâm I(1;3) tiếp xúc với đường thẳng . Hỏi bán kính đường tròn bằng bao nhiêu ?
