Câu hỏi:
19/10/2024 1,399
Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Độ dài cạnh BC là khoảng:
Tam giác ABC có góc A nhọn, AB = 5, AC = 8, diện tích bằng 12. Độ dài cạnh BC là khoảng:
A.
B.
C. 4
D. 5
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
*Phương pháp giải:
- Tính góc A dựa vào công thức tính diện tích tam giác
- Tính BC theo định lý cosin
*Lời giải:
Diện tích tam giác ABC là:
(vì góc A là góc nhọn)
Xét tam giác ABC có AB = 5, AC = 8 và , áp dụng định lí côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
BC2 ≈ 52 + 82 – 2.5.8.cos36°52' ≈ 25
Þ BC ≈ 5.
Vậy BC ≈ 5.
* Các dạng bài tập và lý thuyết thêm giá trị lượng giác
Dạng 1: Tính toán các tỉ số lượng giác, độ dài các cạnh trong tam giác
* Phương pháp giải: Sử dụng các tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán các yếu tố cần thiết.
Dạng 2: So sánh các tỉ số lượng gác, các góc
* Phương pháp giải : Đưa các tỉ số lượng giác về cùng loại, áp dụng tính chất nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtan góc kia và so sánh dựa trên các tính chất:
Nếu hai góc nhọn , có hoặc thì .
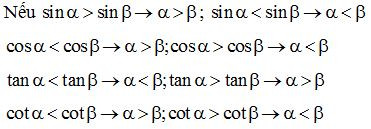
Dạng 3: Rút gọn, tính toán các biểu thức lượng giác
* Phương pháp giải: Áp dụng các tính chất: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtan góc kia. Nếu là một góc nhọn bất kì thì:
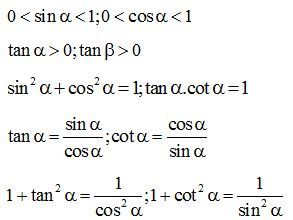
Dạng 4: Chứng minh biểu thức, đẳng thức liên quan đến tỉ số lượng giác
* Phương pháp giải: Áp dụng các tính chất: Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tan góc này bằng côtan góc kia. Nếu là một góc nhọn bất kì thì:
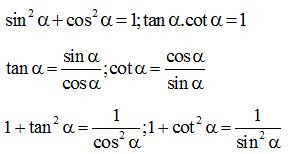
Đối với bài chứng minh biểu thức không phụ thuộc vào giá trị của góc thì cần phải biến đổi sao cho không còn tồn tại các góc trong biểu thức.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giải tam giác. Tính diện tích tam giác – Toán 10 Cánh diều
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.
Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là:
Để đo chiều cao từ mặt đất đến đỉnh cột cờ của một kỳ đài trước Ngọ Môn (Đại Nội – Huế), người ta cắm hai cọc AM và BN cao 1,5 mét so với mặt đất. Hai cọc này song song và cách nhau 10 mét và thẳng hàng so với tim cột cờ (Hình vẽ minh họa). Đặt giác kế tại đỉnh A và B để nhắm đến đỉnh cột cờ, người ta được các góc lần lượt là 51°40' và 45°39' so với đường song song mặt đất.

Chiều cao của cột cờ (làm tròn kết quả đến chữ số thập phân thứ hai) là:
Câu 2:
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Cho hai điểm A, B trên mặt đất sao cho ba điểm A, B và C thẳng hàng. Ta đo được AB = 24 m,
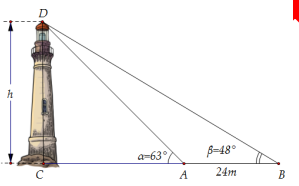
Chiều cao h của tháp gần với giá trị nào sau đây?
Giả sử CD = h là chiều cao của tháp trong đó C là chân tháp. Cho hai điểm A, B trên mặt đất sao cho ba điểm A, B và C thẳng hàng. Ta đo được AB = 24 m,

Chiều cao h của tháp gần với giá trị nào sau đây?
Câu 3:
Vào lúc 9 giờ sáng, hai vận động viên A và B xuất phát từ cùng một vị trí O. Vận động viên A chạy với vận tốc 13 km/h theo một góc so với hướng Bắc là 15°, vận động viên B chạy với vận tốc 12 km/h theo một góc so với hướng Bắc là 135° (hình vẽ).
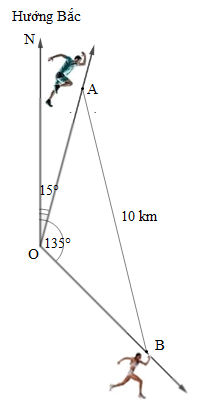
Tại thời điểm nào thì vận động viên A cách vận động viên B một khoảng 10 km (làm tròn kết quả đến phút)?
Câu 4:
Trong sơ đồ, chùm sáng S hướng vào gương màu xanh, phản xạ vào gương màu đỏ và sau đó phản xạ vào gương màu xanh như hình vẽ. Biết OP = 2 m, m.
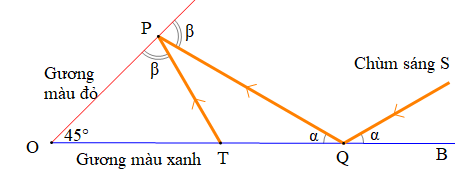
Khi đó đoạn PT bằng:
Câu 6:
Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:
Cho tam giác ABC, biết BC = 24, AC = 13, AB = 15. Số đo góc A là:
Câu 8:
Cho tam giác ABC. Biết AB = 2, BC = 3 và . Chu vi và diện tích tam giác ABC lần lượt là:
Cho tam giác ABC. Biết AB = 2, BC = 3 và . Chu vi và diện tích tam giác ABC lần lượt là:
Câu 9:
Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (AB = 4,3 cm; BC = 3,7 cm; CA = 7,5 cm).
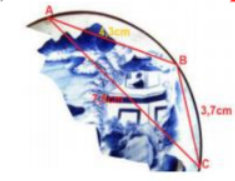
Bán kính của chiếc đĩa này bằng (kết quả làm tròn đến chữ số thập phân thứ hai):
Câu 10:
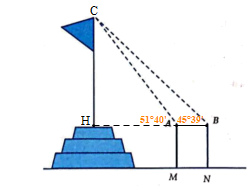
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30' (hình vẽ).
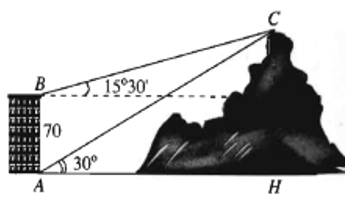
Ngọn núi đó có độ cao CH so với mặt đất gần nhất với giá trị nào sau đây?
Từ hai vị trí A và B của một tòa nhà, người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70 m, phương nhìn AC tạo với phương nằm ngang góc 30°, phương nhìn BC tạo với phương nằm ngang góc 15°30' (hình vẽ).

Ngọn núi đó có độ cao CH so với mặt đất gần nhất với giá trị nào sau đây?
Câu 13:
Tam giác ABC vuông tại B. Trên cạnh AC lấy hai điểm M, N sao cho các góc bằng nhau. Đặt AB = q, BC = m, BM = x, BN = y. Trong các hệ thức sau, hệ thức nào đúng?


