Câu hỏi:
22/10/2024 1,580
Một chiếc đu quay có bán kính 75m, tâm của vòng quay ở độ cao 90m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào Cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay người đó ở độ cao bao nhiêu mét?

Một chiếc đu quay có bán kính 75m, tâm của vòng quay ở độ cao 90m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào Cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay người đó ở độ cao bao nhiêu mét?

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
*Phương pháp giải:
-Từ M kẻ MH Ox, MK Oy
- tìm hoành độ của điểm M ( vị trí sau 20p quay )
- sau 20p quay, độ cao sẽ tính bằng cách cộng thêm với 90
*Lời giải:
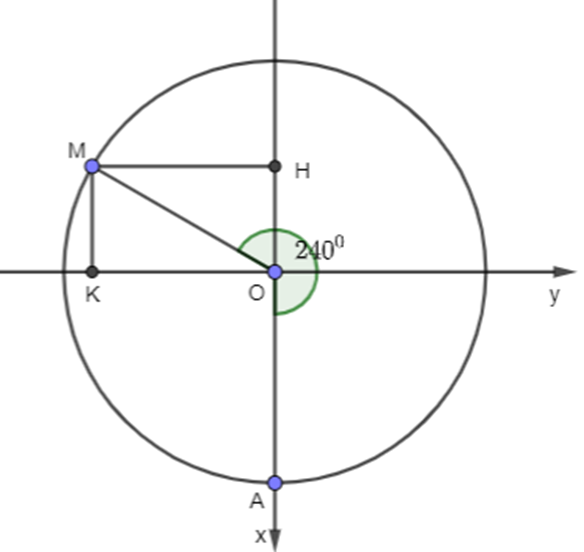
Ta quy hệ trục tọa độ như hình vẽ trên.
A là vị trí cabin thấp nhất. M là vị trí cabin sau 20 phút quay.
Ta có một vòng quay là một vòng tròn nên người đó đi được một vòng nghĩa là quay được một cung tròn lượng giác có số đo 3600.
Vì thời gian thực hiện mỗi vòng quay của đu quay là 30 phút nên mỗi phút người đó quay được một góc lượng giác là: 360:30 = 120.
Sau 20 phút người đó quay được cung lượng giác với điểm đầu là điểm A và điểm cuối là điểm M có số đo 20.12 = 2400.
Từ M kẻ MH Ox, MK Oy
Ta có hoành độ điểm M là: cos2400.OM = cos(1800 – (-600)).75 = - cos(-600).75 = -37,5
Sau 20 phút, người đó ở độ cao: 37,5 + 90 = 127,5 m.
Vậy sau 20 phút cabin của người đó ở độ cao 127,5m.
* Lý thuyết cần nắm và các công thức về giá trị lượng giác của góc:
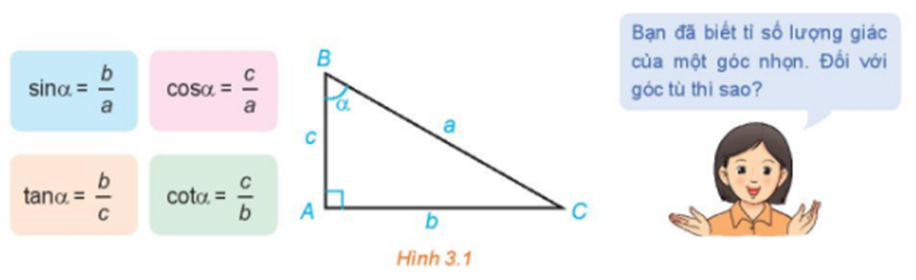
Giá trị lượng giác của một góc
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.
Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x0; y0) trên nửa đường tròn đơn vị để .
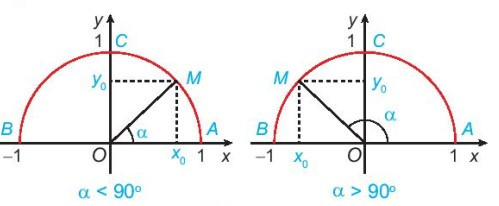
- Định nghĩa tỉ số lượng giác của một góc từ 0o đến 180o
Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho . Khi đó:
+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;
+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;
+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là , được kí hiệu là tan α;
+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là , được kí hiệu là cot α.
- Từ định nghĩa trên ta có:
Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° ‒ α) = sinα;
cos(180° ‒ α) = ‒cosα;
tan(180° ‒ α) = ‒tanα (α ≠ 90°);
cot(180° ‒ α) = ‒cotα (0° < α < 180°).
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giá trị lượng giác của một góc từ 0 độ đến 180 độ – Toán 10 Kết nối tri thức
Giải Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án – Toán lớp 10

Ta quy hệ trục tọa độ như hình vẽ trên.
A là vị trí cabin thấp nhất. M là vị trí cabin sau 20 phút quay.
Ta có một vòng quay là một vòng tròn nên người đó đi được một vòng nghĩa là quay được một cung tròn lượng giác có số đo 3600.
Vì thời gian thực hiện mỗi vòng quay của đu quay là 30 phút nên mỗi phút người đó quay được một góc lượng giác là: 360:30 = 120.
Sau 20 phút người đó quay được cung lượng giác với điểm đầu là điểm A và điểm cuối là điểm M có số đo 20.12 = 2400.
Từ M kẻ MH Ox, MK Oy
Ta có hoành độ điểm M là: cos2400.OM = cos(1800 – (-600)).75 = - cos(-600).75 = -37,5
Sau 20 phút, người đó ở độ cao: 37,5 + 90 = 127,5 m.
Vậy sau 20 phút cabin của người đó ở độ cao 127,5m.
* Lý thuyết cần nắm và các công thức về giá trị lượng giác của góc:
Giá trị lượng giác của một góc
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.
Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x0; y0) trên nửa đường tròn đơn vị để .

- Định nghĩa tỉ số lượng giác của một góc từ 0o đến 180o
Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho . Khi đó:
+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;
+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;
+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là , được kí hiệu là tan α;
+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là , được kí hiệu là cot α.
- Từ định nghĩa trên ta có:
Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° ‒ α) = sinα;
cos(180° ‒ α) = ‒cosα;
tan(180° ‒ α) = ‒tanα (α ≠ 90°);
cot(180° ‒ α) = ‒cotα (0° < α < 180°).
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giá trị lượng giác của một góc từ 0 độ đến 180 độ – Toán 10 Kết nối tri thức
Giải Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án – Toán lớp 10
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2:
Không dùng bảng số hay máy tính cầm tay, tính giá trị các biểu thức sau:
a) (2sin300 + cos1350 – 3tan1500).(cos1800 – cot600);
b) sin2900 + cos21200 + cos200 – tan2600 + cot21350;
c) cos600.sin300 + cos2300.
Chú ý:
Không dùng bảng số hay máy tính cầm tay, tính giá trị các biểu thức sau:
a) (2sin300 + cos1350 – 3tan1500).(cos1800 – cot600);
b) sin2900 + cos21200 + cos200 – tan2600 + cot21350;
c) cos600.sin300 + cos2300.
Chú ý:
Câu 4:
Đơn giản các biểu thức sau:
a) sin1000 + sin800 + cos160 + cos 1640;
b) với .
Đơn giản các biểu thức sau:
a) sin1000 + sin800 + cos160 + cos 1640;
b) với .
Câu 5:
a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
b) Khi , nêu mối quan hệ giữa với hoành độ và tung độ của điểm M.
a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
b) Khi , nêu mối quan hệ giữa với hoành độ và tung độ của điểm M.
Câu 6:
Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau và . Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa và
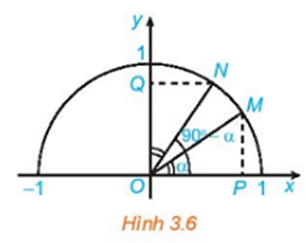
Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau và . Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa và

Câu 7:
Nêu nhận xét về vị trí của hai điểm M và M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa và , giữa và .
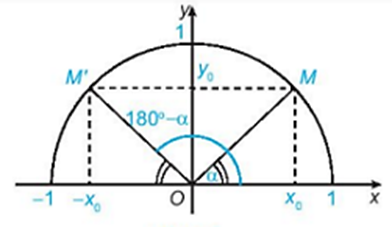
Nêu nhận xét về vị trí của hai điểm M và M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa và , giữa và .