Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ có đáp án
Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ có đáp án
-
359 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
17/07/2024Mở đầu trang 33 SGK Toán 10 tập 1:
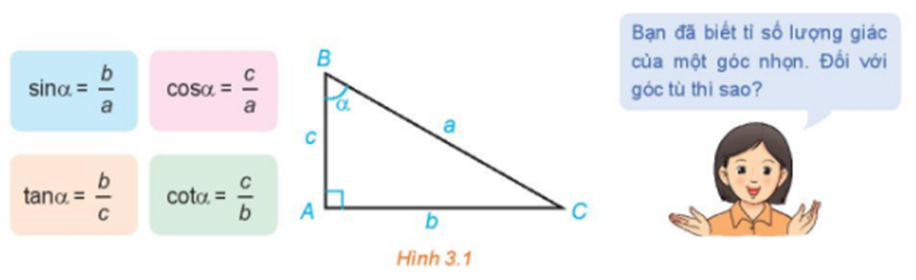
 Xem đáp án
Xem đáp án
Sau bài học này ta sẽ trả lời được:
Để tính tỉ số lượng giác của một góc tù ta sẽ sử dụng công thức lượng giác để chuyển tỉ số lượng giác của góc tù về tỉ số lượng giác của góc nhọn tương ứng.
Câu 2:
23/07/2024a) Nêu nhận xét về vị trí của điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
b) Khi , nêu mối quan hệ giữa với hoành độ và tung độ của điểm M.
 Xem đáp án
Xem đáp án
a)
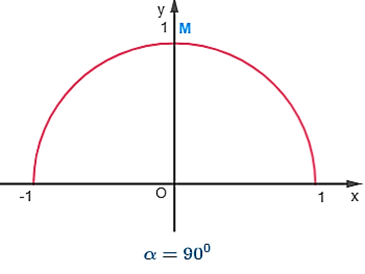
Nếu thì điểm M có tọa độ M(0;1).
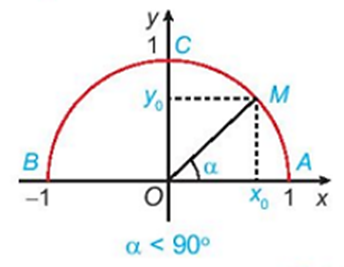
Nếu thì điểm M(x0;y0) nằm trên cung tròn thỏa mãn 0 ≤ x0 ≤ 1, 0 ≤ y0 ≤ 1.
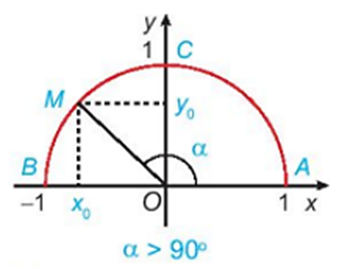
Nếu thì điểm M(x0;y0) nằm trên cung tròn thỏa mãn -1 ≤ x0 ≤ 0, 0 ≤ y0 ≤ 1.
b)
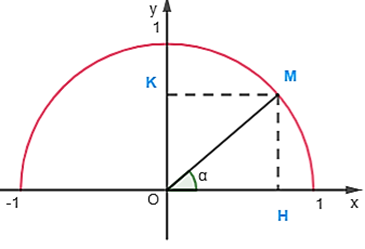
Khi điểm M nằm ở vị trí như hình vẽ.
Kẻ
Xét tam giác vuông MHO, có:
mà OM = 1 nên
Mà MH = |y0| = y0
Ta lại có: mà OM = 1 nên
Mà OH = |x0| = x0
Vậy hoành độ của điểm M bằng giá trị và tung độ của điểm M bằng giá trị .
Câu 3:
23/07/2024Tìm các giá trị lượng giác của góc 1200 (H.3.4).
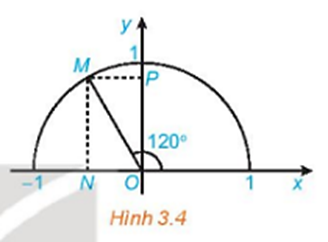
 Xem đáp án
Xem đáp án
Gọi M là điểm trên nửa đường tròn đơn vị sao cho . Gọi H, K tương ứng là hình chiếu vuông của M lên các trục Ox, Oy.
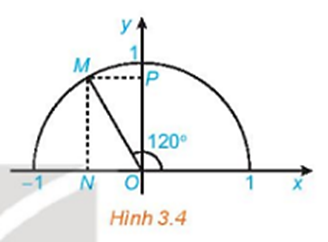
Vì nên
Xét tam giác vuông MON, có:
, .
Mặt khác điểm M nằm bên trái trục tung nên có tọa độ là .
Theo định nghĩa, ta có:
Câu 4:
12/07/2024Nêu nhận xét về vị trí của hai điểm M và M’ đối với trục Oy. Từ đó nêu các mối quan hệ giữa và , giữa và .
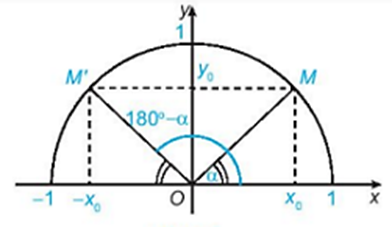
 Xem đáp án
Xem đáp án
Hai điểm M và M’ đối xứng với nhau qua trục Oy.
Ta có:
Ta lại có:
Câu 5:
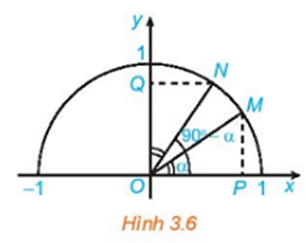
20/07/2024Trong Hình 3.6 hai điểm M, N ứng với hai góc phụ nhau và . Chứng minh rằng ΔMOP = ΔNOQ. Từ đó nêu mối quan hệ giữa và
 Xem đáp án
Xem đáp án
Ta có:
Mà
Xét và , có:
OM = ON = 1
(cmt)
(cạnh huyền – góc nhọn)
⇒ OP = OQ (hai cạnh tương ứng)
Ta có: OP = , OQ =
.
Câu 6:
22/10/2024Một chiếc đu quay có bán kính 75m, tâm của vòng quay ở độ cao 90m (H.3.7), thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào Cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay người đó ở độ cao bao nhiêu mét?

 Xem đáp án
Xem đáp án
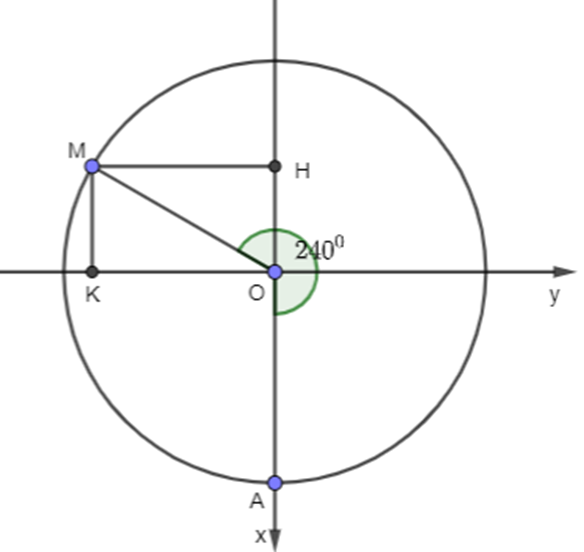
Ta quy hệ trục tọa độ như hình vẽ trên.
A là vị trí cabin thấp nhất. M là vị trí cabin sau 20 phút quay.
Ta có một vòng quay là một vòng tròn nên người đó đi được một vòng nghĩa là quay được một cung tròn lượng giác có số đo 3600.
Vì thời gian thực hiện mỗi vòng quay của đu quay là 30 phút nên mỗi phút người đó quay được một góc lượng giác là: 360:30 = 120.
Sau 20 phút người đó quay được cung lượng giác với điểm đầu là điểm A và điểm cuối là điểm M có số đo 20.12 = 2400.
Từ M kẻ MH Ox, MK Oy
Ta có hoành độ điểm M là: cos2400.OM = cos(1800 – (-600)).75 = - cos(-600).75 = -37,5
Sau 20 phút, người đó ở độ cao: 37,5 + 90 = 127,5 m.
Vậy sau 20 phút cabin của người đó ở độ cao 127,5m.
* Lý thuyết cần nắm và các công thức về giá trị lượng giác của góc:
Giá trị lượng giác của một góc
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị.
Cho trước một góc α, 0° ≤ α ≤ 180°. Khi đó, có duy nhất điểm M(x0; y0) trên nửa đường tròn đơn vị để .
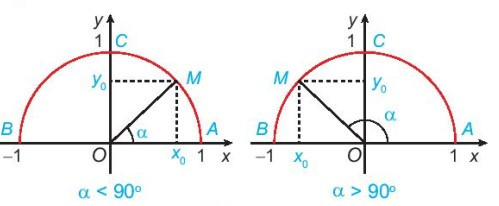
- Định nghĩa tỉ số lượng giác của một góc từ 0o đến 180o
Với mỗi góc α (0° ≤ α ≤ 180°), gọi M(x0; y0) là điểm trên nửa đường tròn đơn vị sao cho . Khi đó:
+ sin của góc α là tung độ y0 của điểm M, được kí hiệu là sin α;
+ côsin của góc α là hoành độ x0 của điểm M, được kí hiệu là cos α;
+ Khi α ≠ 90° (hay x0 ≠ 0), tang của α là , được kí hiệu là tan α;
+ Khi α ≠ 0° và α ≠ 180° (hay y0 ≠ 0), côtang của α là , được kí hiệu là cot α.
- Từ định nghĩa trên ta có:
Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:
sin(180° ‒ α) = sinα;
cos(180° ‒ α) = ‒cosα;
tan(180° ‒ α) = ‒tanα (α ≠ 90°);
cot(180° ‒ α) = ‒cotα (0° < α < 180°).
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Giá trị lượng giác của một góc từ 0 độ đến 180 độ – Toán 10 Kết nối tri thức
Giải Toán 10 Bài 5 (Kết nối tri thức): Giá trị lượng giác của một góc từ 0 độ đến 180 độ
Trắc nghiệm Giá trị lượng giác của một góc bất kì từ 0 độ đến 180 độ có đáp án – Toán lớp 10
Câu 7:
23/07/2024Không dùng bảng số hay máy tính cầm tay, tính giá trị các biểu thức sau:
a) (2sin300 + cos1350 – 3tan1500).(cos1800 – cot600);
b) sin2900 + cos21200 + cos200 – tan2600 + cot21350;
c) cos600.sin300 + cos2300.
Chú ý:
 Xem đáp án
Xem đáp án
a) (2sin300 + cos1350 – 3tan1500).(cos1800 – cot600)
= (2sin300 – cos450 + 3tan300).(-1 – tan300)
b) sin2900 + cos21200 + cos200 – tan2600 + cot21350
= sin2900 + cos2600 + cos200 – tan2600 + cot2450
c) cos600.sin300 + cos2300
Câu 8:
19/07/2024Đơn giản các biểu thức sau:
a) sin1000 + sin800 + cos160 + cos 1640;
b) với .
 Xem đáp án
Xem đáp án
a) sin1000 + sin800 + cos160 + cos 1640
= sin1000 + sin1000 + cos1640 + cos1640
= 2sin1000 + 2cos1640.
b) với .
Câu 9:
22/11/2024Chứng minh các hệ thức sau:
a)
b)
c)
 Xem đáp án
Xem đáp án
*Lời giải
a)

Lấy điểm M trên đường tròn lượng giác sao cho . Từ M kẻ MH Ox và MK Oy. Khi đó:
Xét tam giác OHK vuông tại O, ta có:
OH2 + OK2 = HK2 (Py – ta – go)
Mà HK = OM = 1
⇒ OH2 + OK2 = 1
Hay (đpcm).
b) Ta có:
c) Ta có:
*Phương pháp giải
Vẽ thêm điểm để sử dụng định lý Py-ta-go trong tam giác vuông.
*Lý thuyết cần nắm và dạng toán về công thức lượng giác:
1. Công thức cộng lượng giác
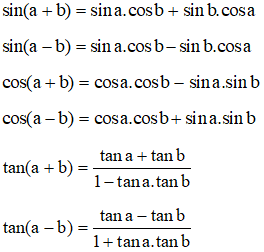
2. Công thức nhân, hạ bậc lượng giác
* Công thức nhân đôi:
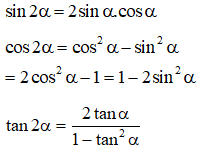
* Công thức hạ bậc:
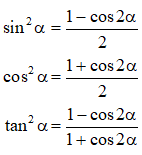
* Công thức nhân ba:
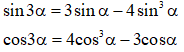
3. Công thức biến đổi tích thành tổng
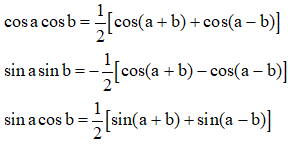
4. Công thức biển đổi tổng thành tích

5. Công thức nghiệm của phương trình lượng giác
a) Phương trình lượng giác cơ bản
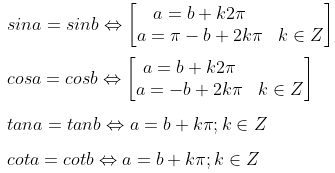
b) Phương trình lượng giác đặc biệt
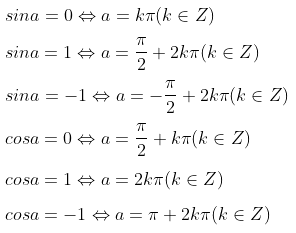
6. Bảng xét dấu của các giá trị lượng giác
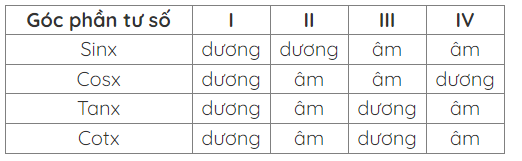
7. Bảng giá trị lương giác của các góc đặc biệt
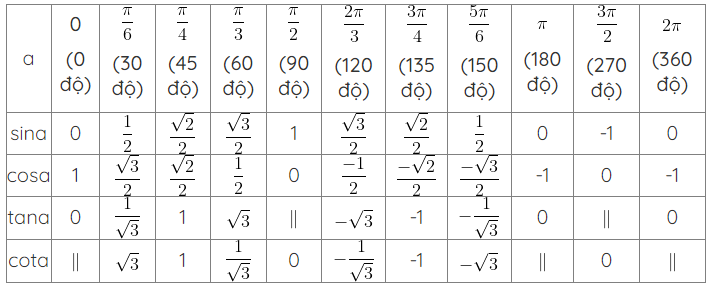
Các dạng bài tập lượng giác
Dạng 1: Tính giá trị lượng giác của góc đặc biệt
a. Phương pháp giải:
- Sử dụng định nghĩa giá trị lượng giá của một góc.
- Sử dụng tính chất và bảng giá trị lượng giác đặc biệt.
- Sử dụng các công thức lượng giác.
Dạng 2: Chứng minh đẳng thức lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để thực hiện phép biến đổi.
Ta lựa chọn một trong các cách biến đổi sau:
* Cách 1: Dùng hệ thức lượng giác biến đổi một vế thành vế còn lại (vế trái thành vế phải hoặc vế phải thành vế trái)
* Cách 2: Biến đổi đẳng thức cần chứng minh về một đẳng thức đã biết là luôn đúng.
* Cách 3: Biến đổi một đẳng thức đã biết là luôn đúng thành đẳng thức cần chứng minh.
Dạng 3: Thu gọn biểu thức lượng giác
a. Phương pháp giải:
Sử dụng công thức lượng giác (công thức cộng, công thức nhân đôi, công thức hạ bậc, công thức biến đổi tổng thành tích, công thức biến đổi tích thành tổng) và các giá trị lượng giác của các góc liên quan đặc biệt để đưa biểu thức ban đầu trở nên đơn giản, ngắn gọn hơn.
Câu 10:
22/07/2024Cho góc thỏa mãn .
Tính giá trị của biểu thức:
 Xem đáp án
Xem đáp án
Chia cả tử và mẫu của biểu thức P cho với ta được:
Vậy với thỏa mãn thì .
Có thể bạn quan tâm
- Trắc nghiệm Toán 10 Bài 5. Giá trị lượng giác của một góc 0 độ đến 180 độ có đáp án (430 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 5. Giá trị lượng giác của một góc 0 độ đến 180 độ có đáp án (271 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 5. Giá trị lượng giác của 1 góc từ 0° đến 180° (phần 2) có đáp án (552 lượt thi)
Các bài thi hot trong chương
- Thi Online Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác (phần 2) có đáp án (577 lượt thi)
- Trắc nghiệm Toán 10 Bài 6. Bài tập cuối chương 3 có đáp án (555 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài ôn tập cuối chương 3 (phần 2) có đáp án (523 lượt thi)
- Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án (502 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án (250 lượt thi)
- Thi Online Trắc nghiệm Toán 10 Bài 6. Bài tập cuối chương 3 có đáp án (239 lượt thi)
