Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án
-
448 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
14/07/2024Tính diện tích tam giác có ba cạnh lần lượt là 5; 12; 13.
Xem đáp án
Đáp án đúng là: B
Nửa chu vi của tam giác là: \(p = \frac{{5 + 12 + 13}}{2} = 15\)
Diện tích của tam giác là:
\(S = \sqrt {p\left( {p - 5} \right)\left( {p - 12} \right)\left( {p - 13} \right)} = \sqrt {15\left( {15 - 5} \right)\left( {15 - 12} \right)\left( {15 - 13} \right)} = 30\).
Câu 2:
21/07/2024Tam giác ABC có \(AC = 3\sqrt 3 \), AB = 3, BC = 6. Tính số đo góc B
Xem đáp án
Đáp án đúng là: A
Áp dụng hệ quả của định lý côsin, ta có: \[\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\]
\[ \Leftrightarrow \cos B = \frac{{B{C^2} + A{B^2} - A{C^2}}}{{2AB.BC}} = \frac{{{6^2} + {3^2} - {{\left( {3\sqrt 3 } \right)}^2}}}{{2.6.3}} = \frac{1}{2} \Rightarrow \widehat B = 60^\circ \].
Câu 3:
22/07/2024Tam giác ABC có các góc \(\widehat A = 75^\circ ,\widehat B = 45^\circ \). Tính tỉ số \(\frac{{AB}}{{AC}}\).
Xem đáp án
Đáp án đúng là: C
Ta có: \[\frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{AB}}{{AC}} = \frac{c}{b} = \frac{{\sin C}}{{\sin B}} = \frac{{\sin (180^\circ - 75^\circ - 45^\circ )}}{{\sin 45^\circ }} = \frac{{\sqrt 6 }}{2}\].
Câu 4:
22/07/2024Tam giác ABC có các góc \(\widehat B = 30^\circ ,\widehat C = 45^\circ \), AB = 3. Tính cạnh AC.
Xem đáp án
Đáp án đúng là: B
Ta có: \[\frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow AC = b = \frac{{c.\sin B}}{{\sin C}} = \frac{{AB.\sin B}}{{\sin C}} = \frac{{3.\sin {{30}^0}}}{{\sin {{45}^0}}} = \frac{{3\sqrt 2 }}{2}\].
Câu 5:
16/07/2024Tam giác ABC có tổng hai góc B và C bằng 135° và độ dài cạnh BC bằng a. Tính bán kính đường tròn ngoại tiếp tam giác.
Xem đáp án
Đáp án đúng là: A
Ta có góc A = 180° – 135° = 45°
\[\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin A}} = \frac{a}{{2\sin 45^\circ }} = \frac{{a\sqrt 2 }}{2}\].
Câu 6:
20/07/2024Tam giác ABC có A = 120° khẳng định nào sau đây đúng?
Xem đáp án
Đáp án đúng là: B
Áp dụng định lí Côsin tại đỉnh A ta có: a2 = b2 + c2 – 2bc.cosA
\[ \Rightarrow \]a2 = b2 + c2 – 2bc.cos120° = b2 + c2 + bc
Câu 7:
16/07/2024Trong tam giác ABC, hệ thức nào sau đây sai?
Xem đáp án
Đáp án đúng là: D
Theo định lí hàm số sin ta có: \[\frac{a}{{\sin A}} = \frac{b}{{{\mathop{\rm sinB}\nolimits} }} = \frac{c}{{{\mathop{\rm sinC}\nolimits} }} = 2R\]
Suy ra:
+ \[\frac{a}{{\sin A}} = \frac{b}{{{\mathop{\rm sinB}\nolimits} }} \Rightarrow a = \frac{{b.\sin A}}{{\sin B}}\]. Do đó đáp án A đúng.
+ \[\frac{a}{{\sin A}} = \frac{c}{{{\mathop{\rm sinC}\nolimits} }} \Rightarrow \sin C = \frac{{c.\sin A}}{a}\]. Do đó đáp án B đúng.
+ \[\frac{a}{{\sin A}} = 2R \Rightarrow a = 2R.\sin A\].Do đó đáp án C đúng.
+ \[\frac{b}{{{\mathop{\rm sinB}\nolimits} }} = 2R \Rightarrow \frac{b}{2} = R\sin B \Rightarrow \frac{b}{{2{\mathop{\rm cosB}\nolimits} }} = R\tan B\]. Do đó đáp án D sai.
Câu 8:
20/07/2024Tính diện tích tam giác ABC biết A = 60°; b = 10; c = 20.
Xem đáp án
Đáp án đúng là: A
Áp dụng công thức : \[S = \frac{1}{2}.bc.\sin A\]\[ = \frac{1}{2}.10.20.\sin 60^\circ \]\[ = 50\sqrt 3 \].
Câu 9:
18/07/2024Cho tam giác ABC có a = 2, \[b = \sqrt 6 \], \[c = \sqrt 3 + 1\]. Tính bán kính R của đường tròn ngoại tiếp.
Xem đáp án
Đáp án đúng là: A
Ta có : \[\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\sqrt 6 }^2} + {{(\sqrt 3 + 1)}^2} - {2^2}}}{{2.\sqrt 6 .(\sqrt 3 + 1)}}\]\[ = \frac{{\sqrt 2 }}{2}\]\[ \Rightarrow \]\(\widehat A\) = 45°.
Do đó : \[R = \frac{a}{{2\sin A}}\]\[ = \frac{2}{{2.\sin 45^\circ }}\]\[ = \sqrt 2 \].
Câu 10:
15/07/2024Tam giác ABC vuông tại A có AB = 6 cm; BC = 10 cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng
Xem đáp án
Đáp án đúng là: C
Ta có \(AC = \sqrt {B{C^2} - A{B^2}} = 8\)(cm).
Diện tích tam giác ABC là:\(S = \frac{1}{2}AB.AC = 24\left( {c{m^2}} \right)\)
Nửa chu vi \(p = \frac{{6 + 8 + 10}}{2} = 12\) (cm)
Suy ra \(r = \frac{S}{p} = \frac{{24}}{{12}} = 2\)(cm).
Câu 11:
28/10/2024Hình bình hành ABCD có AB = a; \(BC = a\sqrt 2 \) và \(\widehat {BAD} = 45^\circ \). Khi đó hình bình hành có diện tích bằng
Xem đáp án
Đáp án đúng: C
*Lời giải
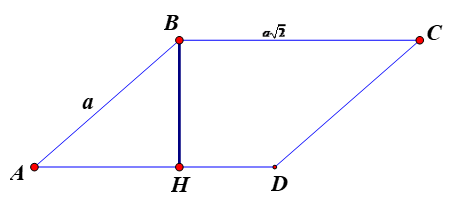
Gọi BH là đường cao của hình bình hành ABCD.
Tam giác BAH vuông tại H, góc \(\widehat {BAH} = \widehat {BAD} = 45^\circ \),
Ta có BH = AB.sin45° = \(\frac{{a\sqrt 2 }}{2}\).
Diện tích hình bình hành ABCD là: \(S = BH.AD = \frac{{a\sqrt 2 }}{2}.a\sqrt 2 = {a^2}\)(đvdt).
*Phương pháp giải
- Vẽ hình bình hành theo dữ kiện bài toán cho
- kẻ đường cao từ B xuống AD
- ta có: tam giác ABH vuông. Áp dụng hệ thức lượng trong tam giác về sin cos, tính độ dài cạnh BH
- từ đó tính ra diện tích hình bình hành = chiều cao * cạnh đáy = BH.AD
* Lý thuyết cần nắm thêm về hệ thức lượng trong tam giác:
Định lí Côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Định lí Côsin. Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
Định lí sin
Trong tam giác ABC: .
Giải tam giác và ứng dụng thực tế
- Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.
Chú ý: Áp dụng định lí côsin, sin và sử dụng máy tính cầm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:
+ Biết hai cạnh và góc xen giữa.
+ Biết ba cạnh.
+ Biết một cạnh và hai góc kề.
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hệ thức lượng trong tam giác – Toán 10 Kết nối tri thức
Sách bài tập Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác
Câu 12:
20/10/2024Tính góc C của tam giác ABC biết a ≠ b và a(a2 – c2) = b(b2 – c2).
Xem đáp án
Đáp án đúng: B
*Phương pháp giải:
- Biến đổi a(a2 – c2) = b(b2 – c2):
+ chuyển về để vế bên phải là số 0. khai triển ra và triệt tiêu dần để thu gọn lại.
+ Áp dụng định lý cosin trong tam giác để tìm ra số đo góc C
*Lời giải:
Ta có: a(a2 – c2) = b(b2 – c2)
⇔ a3 – b3 – c2(a – b) = 0
⇔ (a – b)(a2 + ab + b2) – c2(a – b) = 0
⇔ (a – b)(a2 + ab + b2 – c2) = 0
⇔ a2 + ab + b2 – c2 = 0 (Vì a ≠ b nên a – b ≠ 0)
⇔ a2 + b2 – c2 = – ab
Ta có \[\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{{ - ab}}{{2ab}}\]\[ = - \frac{1}{2}\].
Do đó: \(\widehat C\) = 120°.
* Lý thuyết và các dạng bài toán về hệ thức lượng trong tam giác:
Định lí Côsin
Đối với tam giác ABC, ta thường kí hiệu A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Trong tam giác ABC:
a2 = b2 + c2 – 2bc.cosA.
b2 = c2 + a2 – 2ca.cosB.
c2 = a2 + b2 – 2ab.cosC.
Định lí sin
Trong tam giác ABC: .
Công thức tính diện tích tam giác
Đối với tam giác ABC: A, B, C là các góc của tam giác tại đỉnh tương ứng; a, b, c tương ứng là độ dài của các cạnh đối diện với đỉnh A, B, C; p là nửa chu vi; S là diện tích; R, r tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.
Ta có các công thức tính diện tích tam giác ABC sau:
+) S = pr =
+) S = bc sin A = ca sin B = ab sin C.
+) S =
+) Công thức Heron: S = .
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hệ thức lượng trong tam giác – Toán 10 Kết nối tri thức
Sách bài tập Toán 10 Bài 6 (Kết nối tri thức): Hệ thức lượng trong tam giác
Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án
Câu 13:
20/07/2024Tam giác ABC có các cạnh a; b; c thỏa mãn điều kiện:
(a + b + c)(a + b – c) = 3ab. Khi đó số đo của góc C là.
Xem đáp án
Đáp án đúng là: D
Trong tam giác ABC ta luôn có: c2 = a2 + b2 – 2ab.cosC.
Hệ thức (a + b + c)(a + b – c) = 3ab
⇔ (a + b)2 – c2 = 3ab
⇔ c2 = a2 + b2 – ab
Suy ra: – 2.cosC = – 1 \( \Rightarrow \cos C = \frac{1}{2} \Rightarrow \widehat C = 60^\circ \).
Câu 14:
23/07/2024Tam giác ABC có AB = 7; AC = 5 và \(\cos \left( {B + C} \right) = - \frac{1}{5}\). Tính BC
Xem đáp án
Đáp án đúng là: A
Ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \Leftrightarrow \widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right)\)
\( \Rightarrow \cos \left( {B + C} \right) = \cos \left( {180^\circ - A} \right) = - cosA = - \frac{1}{5}\)
\( \Rightarrow \cos A = \frac{1}{5}\)
Áp dụng định lý côsin trong tam giác, ta có:
\(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.{\mathop{\rm cosA}\nolimits} } = \sqrt {{7^2} + {5^2} - 2.7.5.\frac{1}{5}} = 2\sqrt {15} \).
Câu 15:
14/07/2024Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.
Xem đáp án
Đáp án đúng là: A
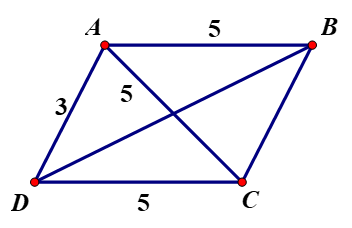
Gọi hình bình hành là ABCD, AD = 3, AB = 5
Gọi α là góc đối diện với đường chéo có độ dài 5
Ta có: \(\cos \alpha = \frac{{{3^2} + {5^2} - {5^2}}}{{2.3.5}} = \frac{3}{{10}}\)
⇒ α là góc nhọn
⇒\(\alpha = \widehat {ADC}\)
⇒ AC = 5
⇒\(B{D^2} = A{D^2} + A{B^2} - 2.AD.AB.\cos \widehat {BAD} = A{D^2} + A{B^2} + 2.AD.AB.\cos \widehat {ADC}\)
(vì \(\widehat {BAD}\) và \(\widehat {ADC}\) bù nhau\( \Rightarrow \cos \widehat {BAD} = - \cos \widehat {ADC}\))
⇒ BD2 = 32 + 52 + 2.3.5.\(\frac{3}{{10}}\) = 43
⇒ BD = \(\sqrt {43} \).