Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án
-
217 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
14/07/2024Tính diện tích tam giác có ba cạnh lần lượt là 5; 12; 13.
Xem đáp án
Đáp án đúng là: B
Nửa chu vi của tam giác là: \(p = \frac{{5 + 12 + 13}}{2} = 15\)
Diện tích của tam giác là:
\(S = \sqrt {p\left( {p - 5} \right)\left( {p - 12} \right)\left( {p - 13} \right)} = \sqrt {15\left( {15 - 5} \right)\left( {15 - 12} \right)\left( {15 - 13} \right)} = 30\).
Câu 2:
21/07/2024Tam giác ABC có \(AC = 3\sqrt 3 \), AB = 3, BC = 6. Tính số đo góc B
Xem đáp án
Đáp án đúng là: A
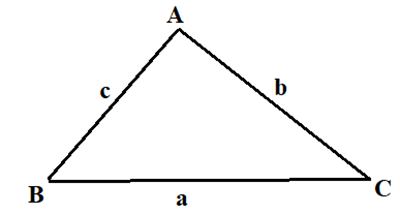
Áp dụng hệ quả của định lý côsin, ta có: \[\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\]
\[ \Leftrightarrow \cos B = \frac{{B{C^2} + A{B^2} - A{C^2}}}{{2AB.BC}} = \frac{{{6^2} + {3^2} - {{\left( {3\sqrt 3 } \right)}^2}}}{{2.6.3}} = \frac{1}{2} \Rightarrow \widehat B = 60^\circ \].
Câu 3:
18/07/2024Tam giác ABC có các góc \(\widehat A = 75^\circ ,\widehat B = 45^\circ \). Tính tỉ số \(\frac{{AB}}{{AC}}\).
Xem đáp án
Đáp án đúng là: C
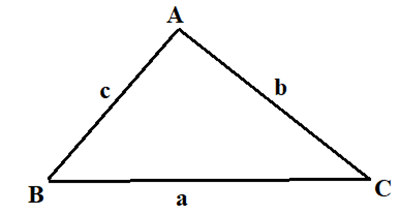
Ta có: \[\frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow \frac{{AB}}{{AC}} = \frac{c}{b} = \frac{{\sin C}}{{\sin B}} = \frac{{\sin (180^\circ - 75^\circ - 45^\circ )}}{{\sin 45^\circ }} = \frac{{\sqrt 6 }}{2}\].
Câu 4:
20/07/2024Tam giác ABC có các góc \(\widehat B = 30^\circ ,\widehat C = 45^\circ \), AB = 3. Tính cạnh AC.
Xem đáp án
Đáp án đúng là: B
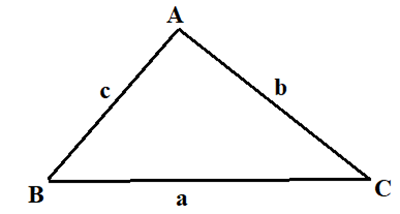
Ta có: \[\frac{b}{{\sin B}} = \frac{c}{{\sin C}} \Rightarrow AC = b = \frac{{c.\sin B}}{{\sin C}} = \frac{{AB.\sin B}}{{\sin C}} = \frac{{3.\sin {{30}^0}}}{{\sin {{45}^0}}} = \frac{{3\sqrt 2 }}{2}\].
Câu 5:
14/07/2024Tam giác ABC có tổng hai góc B và C bằng 135° và độ dài cạnh BC bằng a. Tính bán kính đường tròn ngoại tiếp tam giác.
Xem đáp án
Đáp án đúng là: A
Ta có góc A = 180° – 135° = 45°
\[\frac{{BC}}{{\sin A}} = 2R \Rightarrow R = \frac{{BC}}{{2\sin A}} = \frac{a}{{2\sin 45^\circ }} = \frac{{a\sqrt 2 }}{2}\].
Câu 6:
21/07/2024Tam giác ABC có A = 120° khẳng định nào sau đây đúng?
Xem đáp án
Đáp án đúng là: B
Áp dụng định lí Côsin tại đỉnh A ta có: a2 = b2 + c2 – 2bc.cosA
\[ \Rightarrow \]a2 = b2 + c2 – 2bc.cos120° = b2 + c2 + bc
Câu 7:
14/07/2024Trong tam giác ABC, hệ thức nào sau đây sai?
Xem đáp án
Đáp án đúng là: D
Theo định lí hàm số sin ta có: \[\frac{a}{{\sin A}} = \frac{b}{{{\mathop{\rm sinB}\nolimits} }} = \frac{c}{{{\mathop{\rm sinC}\nolimits} }} = 2R\]
Suy ra:
+ \[\frac{a}{{\sin A}} = \frac{b}{{{\mathop{\rm sinB}\nolimits} }} \Rightarrow a = \frac{{b.\sin A}}{{\sin B}}\]. Do đó đáp án A đúng.
+ \[\frac{a}{{\sin A}} = \frac{c}{{{\mathop{\rm sinC}\nolimits} }} \Rightarrow \sin C = \frac{{c.\sin A}}{a}\]. Do đó đáp án B đúng.
+ \[\frac{a}{{\sin A}} = 2R \Rightarrow a = 2R.\sin A\].Do đó đáp án C đúng.
+ \[\frac{b}{{{\mathop{\rm sinB}\nolimits} }} = 2R \Rightarrow \frac{b}{2} = R\sin B \Rightarrow \frac{b}{{2{\mathop{\rm cosB}\nolimits} }} = R\tan B\]. Do đó đáp án D sai.
Câu 8:
16/07/2024Tính diện tích tam giác ABC biết A = 60°; b = 10; c = 20.
Xem đáp án
Đáp án đúng là: A
Áp dụng công thức : \[S = \frac{1}{2}.bc.\sin A\]\[ = \frac{1}{2}.10.20.\sin 60^\circ \]\[ = 50\sqrt 3 \].
Câu 9:
14/07/2024Cho tam giác ABC có a = 2, \[b = \sqrt 6 \], \[c = \sqrt 3 + 1\]. Tính bán kính R của đường tròn ngoại tiếp.
Xem đáp án
Đáp án đúng là: A
Ta có : \[\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\sqrt 6 }^2} + {{(\sqrt 3 + 1)}^2} - {2^2}}}{{2.\sqrt 6 .(\sqrt 3 + 1)}}\]\[ = \frac{{\sqrt 2 }}{2}\]\[ \Rightarrow \]\(\widehat A\) = 45°.
Do đó : \[R = \frac{a}{{2\sin A}}\]\[ = \frac{2}{{2.\sin 45^\circ }}\]\[ = \sqrt 2 \].
Câu 10:
23/07/2024Tam giác ABC vuông tại A có AB = 6 cm; BC = 10 cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng
Xem đáp án
Đáp án đúng là: C
Ta có \(AC = \sqrt {B{C^2} - A{B^2}} = 8\)(cm).
Diện tích tam giác ABC là:\(S = \frac{1}{2}AB.AC = 24\left( {c{m^2}} \right)\)
Nửa chu vi \(p = \frac{{6 + 8 + 10}}{2} = 12\) (cm)
Suy ra \(r = \frac{S}{p} = \frac{{24}}{{12}} = 2\)(cm).
Câu 11:
11/11/2024Hình bình hành ABCD có AB = a; \(BC = a\sqrt 2 \) và \(\widehat {BAD} = 45^\circ \). Khi đó hình bình hành có diện tích bằng
Xem đáp án
Đáp án đúng là: C
Lời giải
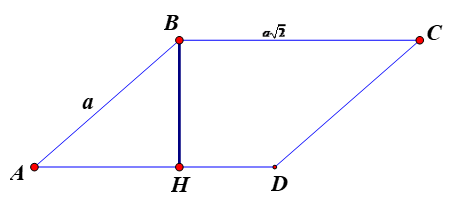
Gọi BH là đường cao của hình bình hành ABCD.
Tam giác BAH vuông tại H, góc \(\widehat {BAH} = \widehat {BAD} = 45^\circ \),
Ta có BH = AB.sin45° = \(\frac{{a\sqrt 2 }}{2}\).
Diện tích hình bình hành ABCD là: \(S = BH.AD = \frac{{a\sqrt 2 }}{2}.a\sqrt 2 = {a^2}\)(đvdt).
*Phương pháp giải:
Tính diện tích tam giác và suy ra diện tích hình bình hành.
*Lý thuyết:
Diện tích hình bình hành
• Diện tích hình bình hành bằng tích của một cạnh với chiều cao ứng với cạnh đó S=a.h.
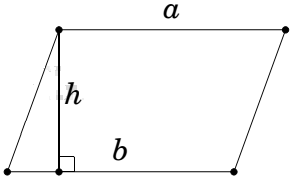
Cho tam giác có BC = a, AC = b, AB = c với:
• là độ dài đường cao lần lượt tương ứng với các cạnh BC, CA, AB
• R là bán kính đường tròn ngoại tiếp tam giác;
• r là bán kính đường tròn nội tiếp tam giác;
• là nửa chu vi tam giác;
• S là diện tích tam giác.
Khi đó ta có các công thức tính diện tích tam giác ABC như sau:
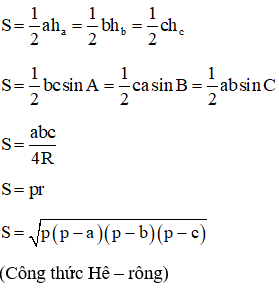
Xem thêm
Các công thức tính diện tích tam giác (2024) đầy đủ, chi tiết nhấtCâu 12:
22/07/2024Tính góc C của tam giác ABC biết a ≠ b và a(a2 – c2) = b(b2 – c2).
Xem đáp án
Đáp án đúng là: B
Ta có: a(a2 – c2) = b(b2 – c2)
⇔ a3 – b3 – c2(a – b) = 0
⇔ (a – b)(a2 + ab + b2) – c2(a – b) = 0
⇔ (a – b)(a2 + ab + b2 – c2) = 0
⇔ a2 + ab + b2 – c2 = 0 (Vì a ≠ b nên a – b ≠ 0)
⇔ a2 + b2 – c2 = – ab
Ta có \[\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}} = \frac{{ - ab}}{{2ab}}\]\[ = - \frac{1}{2}\].
Do đó: \(\widehat C\) = 120°.
Câu 13:
14/07/2024Tam giác ABC có các cạnh a; b; c thỏa mãn điều kiện:
(a + b + c)(a + b – c) = 3ab. Khi đó số đo của góc C là.
Xem đáp án
Đáp án đúng là: D
Trong tam giác ABC ta luôn có: c2 = a2 + b2 – 2ab.cosC.
Hệ thức (a + b + c)(a + b – c) = 3ab
⇔ (a + b)2 – c2 = 3ab
⇔ c2 = a2 + b2 – ab
Suy ra: – 2.cosC = – 1 \( \Rightarrow \cos C = \frac{1}{2} \Rightarrow \widehat C = 60^\circ \).
Câu 14:
21/07/2024Tam giác ABC có AB = 7; AC = 5 và \(\cos \left( {B + C} \right) = - \frac{1}{5}\). Tính BC
Xem đáp án
Đáp án đúng là: A
Ta có: \(\widehat A + \widehat B + \widehat C = 180^\circ \Leftrightarrow \widehat A = 180^\circ - \left( {\widehat B + \widehat C} \right)\)
\( \Rightarrow \cos \left( {B + C} \right) = \cos \left( {180^\circ - A} \right) = - cosA = - \frac{1}{5}\)
\( \Rightarrow \cos A = \frac{1}{5}\)
Áp dụng định lý côsin trong tam giác, ta có:
\(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.{\mathop{\rm cosA}\nolimits} } = \sqrt {{7^2} + {5^2} - 2.7.5.\frac{1}{5}} = 2\sqrt {15} \).
Câu 15:
14/07/2024Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.
Xem đáp án
Đáp án đúng là: A
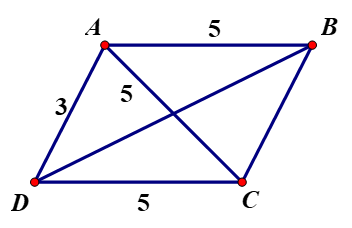
Gọi hình bình hành là ABCD, AD = 3, AB = 5
Gọi α là góc đối diện với đường chéo có độ dài 5
Ta có: \(\cos \alpha = \frac{{{3^2} + {5^2} - {5^2}}}{{2.3.5}} = \frac{3}{{10}}\)
⇒ α là góc nhọn
⇒\(\alpha = \widehat {ADC}\)
⇒ AC = 5
⇒\(B{D^2} = A{D^2} + A{B^2} - 2.AD.AB.\cos \widehat {BAD} = A{D^2} + A{B^2} + 2.AD.AB.\cos \widehat {ADC}\)
(vì \(\widehat {BAD}\) và \(\widehat {ADC}\) bù nhau\( \Rightarrow \cos \widehat {BAD} = - \cos \widehat {ADC}\))
⇒ BD2 = 32 + 52 + 2.3.5.\(\frac{3}{{10}}\) = 43
⇒ BD = \(\sqrt {43} \).