Câu hỏi:
14/07/2024 245
Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.
Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.
A. \(\sqrt {43} \);
A. \(\sqrt {43} \);
B. \(2\sqrt {13} \);
B. \(2\sqrt {13} \);
C. 8;
C. 8;
D. \(8\sqrt 3 \).
D. \(8\sqrt 3 \).
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: A
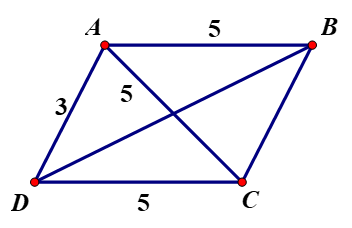
Gọi hình bình hành là ABCD, AD = 3, AB = 5
Gọi α là góc đối diện với đường chéo có độ dài 5
Ta có: \(\cos \alpha = \frac{{{3^2} + {5^2} - {5^2}}}{{2.3.5}} = \frac{3}{{10}}\)
⇒ α là góc nhọn
⇒\(\alpha = \widehat {ADC}\)
⇒ AC = 5
⇒\(B{D^2} = A{D^2} + A{B^2} - 2.AD.AB.\cos \widehat {BAD} = A{D^2} + A{B^2} + 2.AD.AB.\cos \widehat {ADC}\)
(vì \(\widehat {BAD}\) và \(\widehat {ADC}\) bù nhau\( \Rightarrow \cos \widehat {BAD} = - \cos \widehat {ADC}\))
⇒ BD2 = 32 + 52 + 2.3.5.\(\frac{3}{{10}}\) = 43
⇒ BD = \(\sqrt {43} \).
Đáp án đúng là: A
Gọi hình bình hành là ABCD, AD = 3, AB = 5
Gọi α là góc đối diện với đường chéo có độ dài 5
Ta có: \(\cos \alpha = \frac{{{3^2} + {5^2} - {5^2}}}{{2.3.5}} = \frac{3}{{10}}\)
⇒ α là góc nhọn
⇒\(\alpha = \widehat {ADC}\)
⇒ AC = 5
⇒\(B{D^2} = A{D^2} + A{B^2} - 2.AD.AB.\cos \widehat {BAD} = A{D^2} + A{B^2} + 2.AD.AB.\cos \widehat {ADC}\)
(vì \(\widehat {BAD}\) và \(\widehat {ADC}\) bù nhau\( \Rightarrow \cos \widehat {BAD} = - \cos \widehat {ADC}\))
⇒ BD2 = 32 + 52 + 2.3.5.\(\frac{3}{{10}}\) = 43
⇒ BD = \(\sqrt {43} \).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 3:
Hình bình hành ABCD có AB = a; \(BC = a\sqrt 2 \) và \(\widehat {BAD} = 45^\circ \). Khi đó hình bình hành có diện tích bằng
Hình bình hành ABCD có AB = a; \(BC = a\sqrt 2 \) và \(\widehat {BAD} = 45^\circ \). Khi đó hình bình hành có diện tích bằng
Câu 4:
Cho tam giác ABC có a = 2, \[b = \sqrt 6 \], \[c = \sqrt 3 + 1\]. Tính bán kính R của đường tròn ngoại tiếp.
Cho tam giác ABC có a = 2, \[b = \sqrt 6 \], \[c = \sqrt 3 + 1\]. Tính bán kính R của đường tròn ngoại tiếp.
Câu 5:
Tam giác ABC có các góc \(\widehat A = 75^\circ ,\widehat B = 45^\circ \). Tính tỉ số \(\frac{{AB}}{{AC}}\).
Tam giác ABC có các góc \(\widehat A = 75^\circ ,\widehat B = 45^\circ \). Tính tỉ số \(\frac{{AB}}{{AC}}\).
Câu 6:
Tam giác ABC có các cạnh a; b; c thỏa mãn điều kiện:
(a + b + c)(a + b – c) = 3ab. Khi đó số đo của góc C là.
Tam giác ABC có các cạnh a; b; c thỏa mãn điều kiện:
(a + b + c)(a + b – c) = 3ab. Khi đó số đo của góc C là.
Câu 7:
Tính góc C của tam giác ABC biết a ≠ b và a(a2 – c2) = b(b2 – c2).
Tính góc C của tam giác ABC biết a ≠ b và a(a2 – c2) = b(b2 – c2).
Câu 8:
Tam giác ABC có \(AC = 3\sqrt 3 \), AB = 3, BC = 6. Tính số đo góc B
Tam giác ABC có \(AC = 3\sqrt 3 \), AB = 3, BC = 6. Tính số đo góc B
Câu 9:
Tam giác ABC có tổng hai góc B và C bằng 135° và độ dài cạnh BC bằng a. Tính bán kính đường tròn ngoại tiếp tam giác.
Tam giác ABC có tổng hai góc B và C bằng 135° và độ dài cạnh BC bằng a. Tính bán kính đường tròn ngoại tiếp tam giác.
Câu 11:
Tam giác ABC có các góc \(\widehat B = 30^\circ ,\widehat C = 45^\circ \), AB = 3. Tính cạnh AC.
Tam giác ABC có các góc \(\widehat B = 30^\circ ,\widehat C = 45^\circ \), AB = 3. Tính cạnh AC.
Câu 12:
Tam giác ABC vuông tại A có AB = 6 cm; BC = 10 cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng
Tam giác ABC vuông tại A có AB = 6 cm; BC = 10 cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng
Câu 14:
Tam giác ABC có AB = 7; AC = 5 và \(\cos \left( {B + C} \right) = - \frac{1}{5}\). Tính BC
Tam giác ABC có AB = 7; AC = 5 và \(\cos \left( {B + C} \right) = - \frac{1}{5}\). Tính BC
