Câu hỏi:
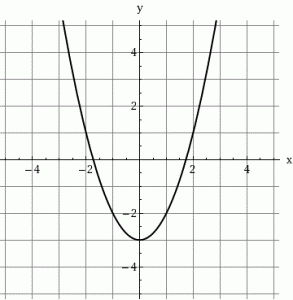
18/07/2024 157Hình vẽ sau là đồ thị của hàm số bậc hai nào ?
A. y = –x2 + 1;
B. y = x2;
C. y = –2x2;
D. y = –x2.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D.
Hàm số bậc hai có dạng y = ax2 + bx + c (a ≠ 0).
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng xuống, đỉnh I(0; 0) và cắt trục tung tại điểm (0; 0).
Do đó ta có:
a < 0
−b2a=0 ⇒ b = 0
c = 0
Dựa vào đồ thị ta còn thấy, đồ thị hàm số đi qua điểm (1; –1) do đó ta có:
Tại x = 1 thì y = a.12 + b.1 + c = –1
Hay a + b + c = –1
Mà b = 0, c = 0
⇒ a = –1 (TM)
Vậy hàm số y = ax2 + bx + c là y = –x2.
Hướng dẫn giải:
Đáp án đúng là: D.
Hàm số bậc hai có dạng y = ax2 + bx + c (a ≠ 0).
Dựa vào hình vẽ, ta thấy đồ thị hàm số y = ax2 + bx + c có bề lõm hướng xuống, đỉnh I(0; 0) và cắt trục tung tại điểm (0; 0).
Do đó ta có:
a < 0
−b2a=0 ⇒ b = 0
c = 0
Dựa vào đồ thị ta còn thấy, đồ thị hàm số đi qua điểm (1; –1) do đó ta có:
Tại x = 1 thì y = a.12 + b.1 + c = –1
Hay a + b + c = –1
Mà b = 0, c = 0
⇒ a = –1 (TM)
Vậy hàm số y = ax2 + bx + c là y = –x2.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
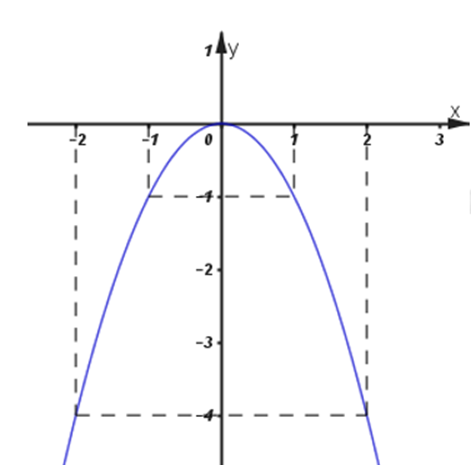
Câu 2:
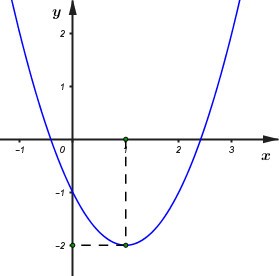
Cho hàm số y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới đây.
Công thức hàm số của đồ thị trên là:
Cho hàm số y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới đây.

Công thức hàm số của đồ thị trên là:
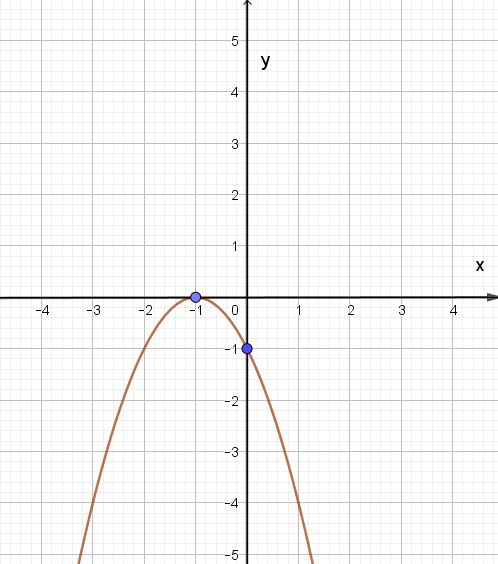
Câu 3:
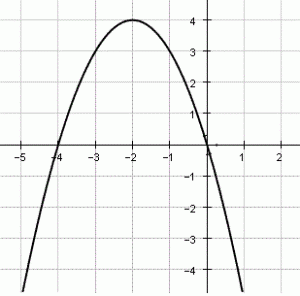
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.
Khi đó 2a + b + 2c bằng:
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.

Khi đó 2a + b + 2c bằng:
Câu 4:
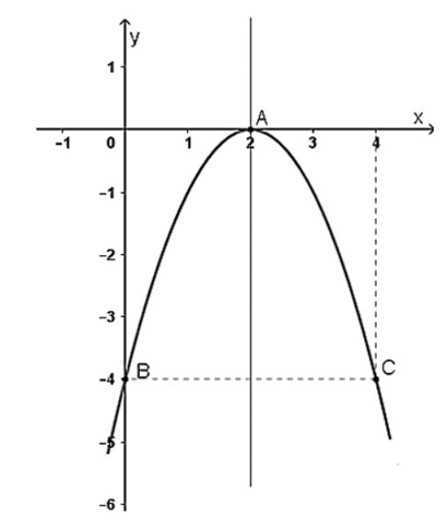
Cho hàm số y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới. Xác định hàm số đó.
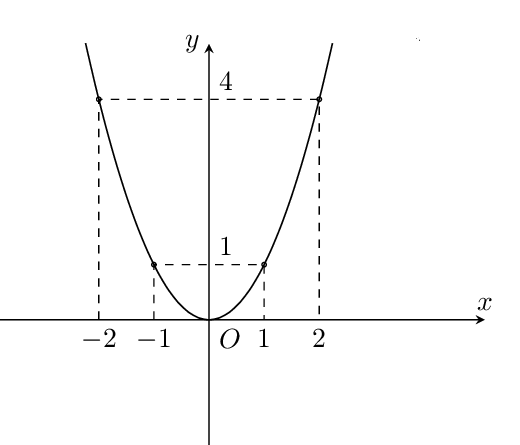
Câu 5:
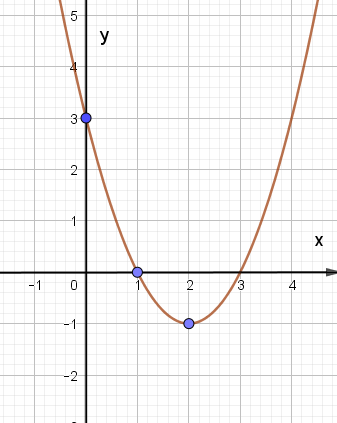
Cho đồ thị hàm số y = ax2 + bx + c (a ≠ 0) trong hình vẽ sau. Xác định hàm số đó.
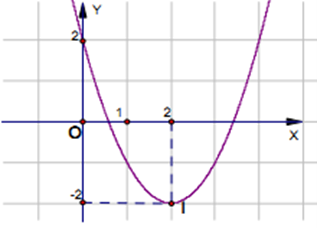
Cho đồ thị hàm số y = ax2 + bx + c (a ≠ 0) trong hình vẽ sau. Xác định hàm số đó.

Câu 6:
Cho hàm số y = ax2 + bx + c (a ≠ 0) có đồ thị là parabol trong hình dưới. Xác định hàm số đó.
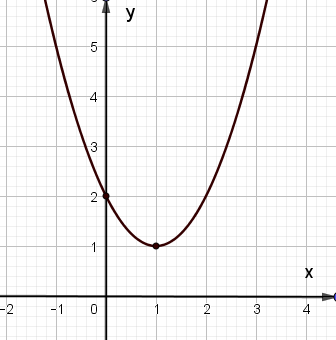

Câu 7:
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.
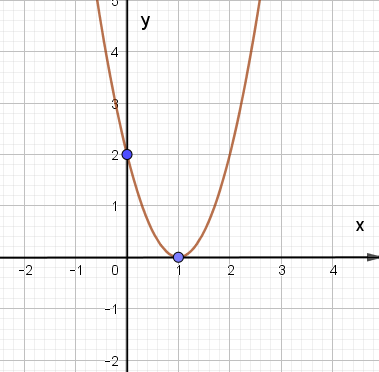
Xác định công thức của hàm số đó.
Cho hàm số bậc hai y = ax2 + bx + c (a ≠ 0) có đồ thị như hình dưới.

Xác định công thức của hàm số đó.