Hàm số nào sau đây không liên tục trên R

Đáp án đúng là: B

*Lời giải:

Dễ thấy đáp án là B

Xét  A có $x^2+1>\mathrm{1,}\forall x\in ℝ\Rightarrow TXĐ:x=2017D=ℝ$   

Xét B có  $x+2\ne 0\iff x\ne 2\Rightarrow TXĐ:D=ℝ\backslash \left\{2\right\}$

Tương tự  C;D

*Phương pháp giải:

 a) Hàm số đa thức liên tục trên toàn bộ tập số thực .

 b) Hàm số phân thức hữu tỉ và hàm số lượng giác liên tục trên từng khoảng xác định của chúng.

*Một số lý thuyết liên quan:

1. HÀM SỐ LIÊN TỤC TẠI MỘT ĐIỂM

Định nghĩa 1

Cho hàm số y = f(x) xác định trên khoảng K và x₀ ∈ K.

Hàm số y = f(x) được gọi là liên tục tại x₀ nếu $\underset{\mathrm{x}\to {\mathrm{x}}_0}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left({\mathrm{x}}_0\right).$

2. HÀM SỐ LIÊN TỤC TRÊN MỘT KHOẢNG

Định nghĩa 2

Hàm số y = f(x) được gọi là liên tục trên một khoảng nếu nó liên tục tại mọi điểm của khoảng đó.

Hàm số y = f(x) được gọi là liên tục trên đoạn [a; b] nếu nó liên tục trên khoảng (a; b) và $\underset{\mathrm{x}\to {\mathrm{a}}^{+}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{a}\right),\underset{\mathrm{x}\to {\mathrm{b}}^{-}}{\lim }\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{b}\right).$

Nhận xét: Đồ thị của hàm số liên tục trên một khoảng là một đường liền trên khoảng đó.

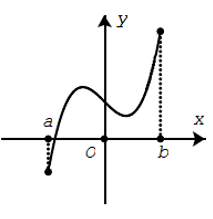
Hàm số liên tục trên khoảng (a;b)

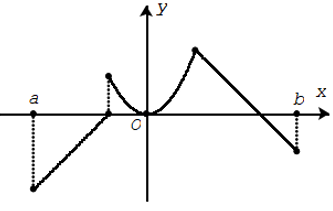
Hàm số không liên tục trên khoảng (a; b).

Định lí 2

Giả sử y = f(x) và y = g(x) là hai hàm số liên tục tại điểm x₀. Khi đó:

a) Các hàm số y = f(x) + g(x), y = f(x) – g(x) và y = f(x).g(x) liên tục tại x₀;

b) Hàm số $\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{g}\left(\mathrm{x}\right)}$ liên tục tại x₀ nếu g(x₀) ≠ 0.

Xem thêm các bài viết liên quan hay, chi tiết:

50 bài tập về Hàm số liên tục (có đáp án 2024) và cách giải 

Hàm số liên tục | Lý thuyết, công thức, các dạng bài tập và cách giải

Dùng định nghĩa, xét tính liên tục của hàm số: a) f(x) = x^3 ‒ 3x + 2 tại điểm x = ‒2