Câu hỏi:
12/10/2024 120
Hàm số nào dưới đây không có cực trị?
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: C
*Phương pháp giải: Quy tắc tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệuxi (i=1,2,3,...)là các nghiệm của nó.
Bước 3. Tính f''(x) và f''(xi ) .
Bước 4. Dựa vào dấu của f''(xi )suy ra tính chất cực trị của điểm xi.
*Lời giải:
Xét hàm số có . Do đó hàm số không có cực trị
* Một số lý thuyết liên quan:
1. Định nghĩa: Cho hàm số y = f(x)xác định và liên tục trên khoảng (a;b) (có thể a là -∞; b là +∞) và điểm x0∈(a;b).
Nếu tồn tại số h > 0 sao cho f(x)< f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x≠x_0 thì ta nói hàm số f(x) đạt cực đại tại x0.
Nếu tồn tại số h >0 sao cho f(x) >f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x ≠ x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.
2. Điều kiện đủ để hàm số có cực trị: Giả sử hàm số y=f(x) liên tục trên
K=(x0 - h;x0 + h)và có đạo hàm trên K hoặc trên K\{x0}, với h >0.
Nếu f'(x)> 0 trên khoảng (x0 - h;x0) và f'(x) <0 trên (x0;x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
Nếu f'(x) < 0 trên khoảng (x0 - h;x0) và f'(x) >0 trên (x0;x0+ h) thì x0 là một điểm cực tiểu của hàm số f(x).
Minh họa bằng bảng biến thiến
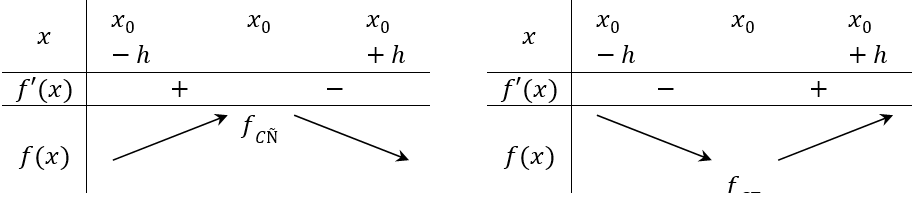
Chú ý: Nếu hàm số y=f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCÑ (fCT), còn điểm M(x0;f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
Xem thêm các bài viết liên quan hay, chi tiết:
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau: a) y = x^3 - 3x^2 + 3x - 1
Đáp án đúng là: C
*Phương pháp giải: Quy tắc tìm cực trị của hàm số
Quy tắc 1:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tínhf'(x). Tìm các điểm tại đó f'(x)bằng 0 hoặc f'(x) không xác định.
Bước 3. Lập bảng biến thiên.
Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.
Quy tắc 2:
Bước 1. Tìm tập xác định của hàm số.
Bước 2. Tính f'(x). Giải phương trình f'(x)và ký hiệuxi (i=1,2,3,...)là các nghiệm của nó.
Bước 3. Tính f''(x) và f''(xi ) .
Bước 4. Dựa vào dấu của f''(xi )suy ra tính chất cực trị của điểm xi.
*Lời giải:
Xét hàm số có . Do đó hàm số không có cực trị
* Một số lý thuyết liên quan:
1. Định nghĩa: Cho hàm số y = f(x)xác định và liên tục trên khoảng (a;b) (có thể a là -∞; b là +∞) và điểm x0∈(a;b).
Nếu tồn tại số h > 0 sao cho f(x)< f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x≠x_0 thì ta nói hàm số f(x) đạt cực đại tại x0.
Nếu tồn tại số h >0 sao cho f(x) >f(x0 ) với mọi x ∈ (x0 - h;x0 + h) và x ≠ x0 thì ta nói hàm số f(x) đạt cực tiểu tại x0.
2. Điều kiện đủ để hàm số có cực trị: Giả sử hàm số y=f(x) liên tục trên
K=(x0 - h;x0 + h)và có đạo hàm trên K hoặc trên K\{x0}, với h >0.
Nếu f'(x)> 0 trên khoảng (x0 - h;x0) và f'(x) <0 trên (x0;x0 + h) thì x0 là một điểm cực đại của hàm số f(x).
Nếu f'(x) < 0 trên khoảng (x0 - h;x0) và f'(x) >0 trên (x0;x0+ h) thì x0 là một điểm cực tiểu của hàm số f(x).
Minh họa bằng bảng biến thiến
Chú ý: Nếu hàm số y=f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, kí hiệu là fCÑ (fCT), còn điểm M(x0;f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị hàm số.
Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
Xem thêm các bài viết liên quan hay, chi tiết:
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau: a) y = x^3 - 3x^2 + 3x - 1
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho khối lăng trụ đứng ABC.A'B'C' có đáy là tam giác cân tại A và , cạnh bên AA' = a, góc giữa A'B và mặt phẳng (ABC) bằng 60o. Thể tích khối lăng trụ đã cho bằng
Câu 2:
Cho hình chóp tứ giác đều S.ABCD có góc giữa cạnh bên với đáy một góc 45o. Tính cosin của góc giữa mặt bên và đáy của hình chóp đã cho.
Cho hình chóp tứ giác đều S.ABCD có góc giữa cạnh bên với đáy một góc 45o. Tính cosin của góc giữa mặt bên và đáy của hình chóp đã cho.
Câu 3:
Cho tập M gồm các số tự nhiên có ba chữ số đôi một khác nhau lấy từ tập {0; 1; 2; 3; 4; 5}. Chọn ngẫu nhiên một số từ tập M. Tính xác xuất để số được chọn có chữ số hàng trăm nhỏ hơn chữ số hàng chục.
Câu 4:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu . Tìm tất cả các giá trị thực dương của tham số m để mặt phẳng x - 2y + 2z + m = 0 tiếp xúc với mặt cầu (S)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu . Tìm tất cả các giá trị thực dương của tham số m để mặt phẳng x - 2y + 2z + m = 0 tiếp xúc với mặt cầu (S)
Câu 7:
Cho hàm số f(x) xác định và có đạo hàm cấp hai trên thỏa mãn f(0) = 0, và . Tính f(2)
Câu 8:
Cho khối nón có đường kính đáy bằng 4a và chiều cao bằng 2a. Thể tích của khối nón đã cho bằng
Cho khối nón có đường kính đáy bằng 4a và chiều cao bằng 2a. Thể tích của khối nón đã cho bằng
Câu 9:
Hình chiếu vuông góc của điểm M(1;-2;3) lên mặt phẳng (Oyz) có toạ độ là:
Hình chiếu vuông góc của điểm M(1;-2;3) lên mặt phẳng (Oyz) có toạ độ là:
Câu 10:
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 2a và SA vuông góc với đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SBD).
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 2a và SA vuông góc với đáy. Tính theo a khoảng cách từ A đến mặt phẳng (SBD).
Câu 12:
Cho khối chóp tam giác đều S.ABC có cạnh đáy AB=2a, cạnh bên . Thể tích khối chóp đã cho bằng:
Cho khối chóp tam giác đều S.ABC có cạnh đáy AB=2a, cạnh bên . Thể tích khối chóp đã cho bằng:
Câu 13:
Biết x, y là các số thực thỏa mãn với mọi số thực a > 0. Tìm giá trị lớn nhất của biểu thức P = 3x + 4y
Câu 14:
Từ các chữ số 0, 1, 2, 3, 4, 5, 6 lập được bao nhiêu số chẵn gồm ba chữ số đôi một khác nhau?
Câu 15:
Trong không gian với hệ tọa độ Oxyz cho mặt cầu và mạt phẳng (P): x + y + 2z + 5 = 0. Lấy điểm A di động trên (S) và điểm B di động trên (S) sao cho cùng phương . Tìm giá trị lớn nhất của độ dài đoạn AB.
Trong không gian với hệ tọa độ Oxyz cho mặt cầu và mạt phẳng (P): x + y + 2z + 5 = 0. Lấy điểm A di động trên (S) và điểm B di động trên (S) sao cho cùng phương . Tìm giá trị lớn nhất của độ dài đoạn AB.



![Cho hàm số y = f(x) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của m để phương trình 2^ f(x) + 4/ f(x) + log 2 [f^2(x) - 4f(x) + 5] = m có 6 nghiệm thực phân biệt? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid5-1683269005.png)
![Cho hàm số y = f(x) có bảng biến thiên của f'(x) như sau: Có bao nhiêu giá trị nguyên của m trên đoạn [-2022;2023] để hàm số g(x) = f(x^3/9) - m(x^2 + 9)^2/18 nghịch biến trên khoảng (0;5)? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2023/05/blobid3-1683268811.png)