Số giao điểm của đồ thị hàm số $y=x^3+2x+\text{ln}x$ với đường thẳng y = x + 2 là:

Đáp án đúng: B

* Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số $y=x^3+2x+\text{ln}x$ với đường thẳng y = x + 2 là $x^3+2x+\text{ln}x=x+2$.

Điều kiện x > 0.

Khi đó phương trình trở thành $x^3+x+\text{ln}x-2=0$.

Xét hàm số $f\left(x\right)=x^3+x+\text{ln}x-2$, với x > 0.

Ta có $f^{\text{'}}\left(x\right)=3x^2+1+\frac{1}{x}>0,\forall x>0$. Do đó hàm số $f\left(x\right)=x^3+x+\text{ln}x-2$ đồng biến trên khoảng $\left(0;+\infty \right)$.

Khi đó phương trình $x^3+x+\text{ln}x-2=0$ có nhiều nhất là 1 nghiệm.

Nhận thấy x = 1 là nghiệm của phương trình.

Vậy đồ thị hàm số $y=x^3+2x+\text{ln}x$ với đường thẳng y = x + 2 có 1 giao điểm.

* Phương pháp giải:

 - để tìm được giao điểm của 2 đồ thị hàm số: ta sẽ tìm hoành độ giao điểm của 2 đồ thị hàm số

- xét hám số thu được. tính đạo hàm của hàm số và xét bảng biến thiên xem sự đồng biến/nghịch biến. từ đó suy ra nghiệm chính là số giao điểm 

* Lý thuyết cần nắm thêm về sự tương giao giữa đồ thị hàm số

Cho hàm số y = f (x) có đồ thị (C₁) và y = g (x) có đồ thị (C₂) .

Phương trình hoành độ giao điểm của (C₁) và (C₂) là f (x) = g (x).

Khi đó:

- Số giao điểm của (C₁) và (C₂) bằng với số nghiệm của phương trình (1) .

- Nghiệm x₀ của phương trình (1) chính là hoành độ x₀ của giao điểm.

- Để tính tung độ y₀ của giao điểm, ta thay hoành độ x₀ vào y = f (x).

- Điểm M (x₀ ; y₀) là giao điểm của (C₁) và (C₂).

CÁC DẠNG TOÁN HAY GẶP VÀ CÁC KỸ NĂNG CẦN THIẾT.

Dạng 1. Tìm toạ độ giao điểm của các đồ thị hàm số cho trước.

Phương pháp giải.

Cho 2 hàm số $y=f\left(x\right),y=g\left(x\right)$ có đồ thị lần lượt là (C) và (C’).

Bước 1: Lập phương trình hoành độ giao điểm của (C) và (C’): $f\left(x\right)=g\left(x\right)$

Bước 2: Giải phương trình tìm x từ đó suy ra y và toạ độ giao điểm.

Bước 3: Số nghiệm của (*) là số giao điểm của (C) và (C’). Thay trở lại $y=f\left(x\right)(y=g(x\left)\right)$, ta sẽ được toạ độ giao điểm.

Dạng 2. Tìm m để sự tương giao của các đồ thị hàm số thoả mãn điều kiện cho trước.

Phương pháp giải.

BÀI TOÁN 1: TƯƠNG GIAO CỦA ĐỒ THỊ HÀM BẬC 3.

Phương pháp 1: Bảng biến thiên (đồ thị hàm số).

+) Lập phương trình hoành độ giao điểm dạng $F\left(x,m\right)=0$ (phương trình ẩn x tham số m)

+) Cô lập m đưa phương trình về dạng $m=f\left(x\right)$

+) Lập BBT cho hàm số $y=f\left(x\right)$.

+) Dựa và giả thiết và BBT từ đó suy ra m.

* Dấu hiệu: Sử dụng phương pháp bảng biến thiên khi m độc lập với x.

Phương pháp 2: Nhẩm nghiệm – tam thức bậc 2.

+) Lập phương trình hoành độ giao điểm $F\left(x,m\right)=0$

+) Nhẩm nghiệm: (Khử tham số). Giả sử $x=x_0$ là 1 nghiệm của phương trình.

+) Phân tích:

$$\begin{gathered} F\left(x,m\right)=0\iff \left(x-x_0\right).g\left(x\right)=0 \\ \iff \left[\begin{array}{l}x=x_0\\ g\left(x\right)=0\end{array}\right. \end{gathered}$$

(là $g\left(x\right)=0$ là phương trình bậc 2 ẩn x tham số m ).

+) Dựa vào yêu cầu bài toán đi xử lý phương trình bậc 2: $g\left(x\right)=0$.

Phương pháp 3: Cực trị.

* Nhận dạng: Khi bài toán không cô lập được m và cũng không nhẩm được nghiệm.

* Quy tắc:

- Lập phương trình hoành độ giao điểm $F\left(x,m\right)=0$ (1). Xét hàm số $y=F\left(x,m\right)$.

- Để (1) có đúng 1 nghiệm thì đồ thị $y=F\left(x,m\right)$ cắt trục hoành tại đúng 1 điểm. (2TH)

+ Hoặc hàm số luôn đơn điệu trên R $\iff$ hàm số không có cực trị $\iff y\text{'}=0$ hoặc vô nghiệm hoặc có nghiệm kép $\iff {\Delta }_{y\text{'}}\le 0$

+ Hoặc hàm số có CĐ, CT và $y_{cd}.y_{ct}>0$

Mở rộng: Tìm m để đồ thị hàm bậc 3 cắt trục hoành tại 3 điểm lập thành 1 cấp số cộng.

1. Định lí Vi - ét.

*) Cho bậc 2: Cho phương trình $a{x}^2+bx+c=0$ có 2 nghiệm $x_1,x_2$ thì ta có:

$\begin{array}{l}{x}_1+x_2=-\frac{b}{a}\\ x_1{x}_2=\frac{c}{a}\end{array}$

*) Cho bậc 3: Cho phương trình $a{x}^3+b{x}^2+cx+d=0$ có 3 nghiệm $x_1,x_2,x_3$ thì ta có:

$\begin{array}{l}{x}_1+x_2+x_3=-\frac{b}{a},\\ x_1{x}_2+x_2{x}_3+x_3{x}_1=\frac{c}{a},\\ x_1{x}_2{x}_3=-\frac{d}{a}\end{array}$

2.Tính chất của cấp số cộng: Cho 3 số a,b,c theo thứ tự đó lập thành 1 cấp số cộng thì:

a + c = 2b

+) Điều kiện cần: $x_0=-\frac{b}{3a}$ là 1 nghiệm của phương trình. Từ đó thay vào phương trình để tìm m.

+) Điều kiện đủ: Thay m tìm được vào phương trình và kiểm tra

BÀI TOÁN 2: TƯƠNG GIAO CỦA HÀM SỐ PHÂN THỨC.

Phương pháp : Cho hàm số $y=\frac{ax+b}{cx+d}\left(C\right)$ và đường thẳng $d:y=px+q$. Phương trình hoành độ giao điểm của (C) và (d): $\frac{ax+b}{cx+d}=px+q\iff F\left(x,m\right)=0$ (phương trình bậc 2 ẩn x tham số m).

* Các câu hỏi thường gặp:

1. Tìm m để d cắt (C) tại 2 điểm phân biệt $\iff$(1) có 2 nghiệm phân biệt khác $-\frac{d}{c}$

2. Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh phải của (C) $\iff$ (1) có 2 nghiệm phân biệt $x_1,x_2$ và thỏa mãn $:-\frac{d}{c}<x_1^{}<x_2$.

3. Tìm m để d cắt (C) tại 2 điểm phân biệt cùng thuộc nhánh trái của (C) $\iff$(1) có 2 nghiệm phân biệt $x_1,x_2$ và thỏa mãn $x_1^{}<x_2<-\frac{d}{c}$.

4. Tìm m để d cắt (C) tại 2 điểm phân biệt thuộc 2 nhánh của (C) $\iff$ (1) có 2 nghiệm phân biệt $x_1,x_2$ và thỏa mãn $x_1^{}<-\frac{d}{c}<x_2$.

5. Tìm m để d cắt (C) tại 2 điểm phân biệt A và B thỏa mãn điều kiện hình học cho trước:

+) Đoạn thẳng AB = k

+) Tam giác ABC vuông.

+) Tam giác ABC có diện tích $S_0$

* Chú ý: Công thức tính khoảng cách:

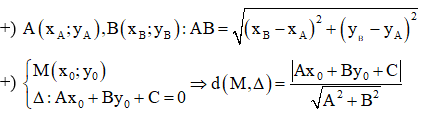
Xem thêm các bài viết liên quan hay, chi tiết:

Toán 12 Bài 4 (Kết nối tri thức): Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Toán 12 (Kết nối tri thức) Bài tập cuối chương 1 trang 42

50 bài toán về tương giao của đồ thị hàm số (có đáp án 2024) – Toán 12