Câu hỏi:
13/07/2024 122
Hàm số \(f(x) = \frac{3}{{\sqrt {x - 4} }}\) có tập xác định là:
Hàm số \(f(x) = \frac{3}{{\sqrt {x - 4} }}\) có tập xác định là:
A. [4; +∞);
B. ℝ \ {4};
C. (4; +∞);
Đáp án chính xác
D. ℝ.
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C.
Điều kiện xác định của hàm số \(f(x) = \frac{3}{{\sqrt {x - 4} }}\) là: x – 4 > 0 ⇔ x > 4
Vậy tập xác định của hàm số \(f(x) = \frac{3}{{\sqrt {x - 4} }}\) là D = (4; +∞).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 4:
Tập xác định của hàm số \(f(x) = \frac{{x + 3}}{{{x^2} + 1}}\) là:
Tập xác định của hàm số \(f(x) = \frac{{x + 3}}{{{x^2} + 1}}\) là:
Xem đáp án »
13/07/2024
137
Câu 6:
Cho hàm số \(f(x) = \sqrt {2x + 7} \).
Tìm tập xác định của hàm số.
Cho hàm số \(f(x) = \sqrt {2x + 7} \).
Tìm tập xác định của hàm số.
Xem đáp án »
23/07/2024
132
Câu 7:
Cho hàm số \(f(x) = \sqrt {2x + 7} \).
Tìm tập giá trị của hàm số.
Cho hàm số \(f(x) = \sqrt {2x + 7} \).
Xem đáp án »
13/07/2024
131
Câu 11:
Tập giá trị của hàm số: \(f(x) = \frac{{2022}}{{\sqrt {2x - 2} }}\) là:
Tập giá trị của hàm số: \(f(x) = \frac{{2022}}{{\sqrt {2x - 2} }}\) là:
Xem đáp án »
13/07/2024
113
Câu 12:
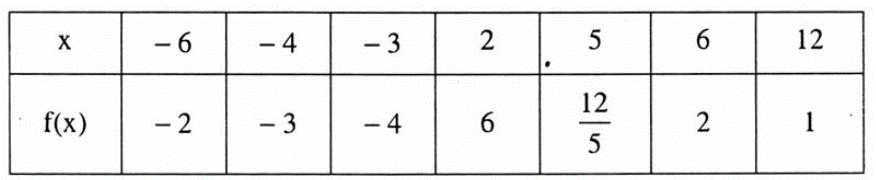
Hàm số v = f(t) được cho bởi bảng như sau:
Tìm tập xác định của hàm số này.
Hàm số v = f(t) được cho bởi bảng như sau:
Tìm tập xác định của hàm số này.
Xem đáp án »
21/07/2024
111
