Câu hỏi:
23/11/2024 15,490
Elip \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) có độ dài trục lớn bằng:
Elip \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) có độ dài trục lớn bằng:
A. 5;
A. 5;
B. 10;
B. 10;
C. 25;
C. 25;
D. 50.
D. 50.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Lời giải
Gọi phương trình của Elip là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,\) có độ dài trục lớn \({A_1}{A_2} = \) 2a.
Xét \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) \( \Rightarrow \left\{ \begin{array}{l}{a^2} = 25\\{b^2} = 9\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}a = 5\\b = 3\end{array} \right.\,\,\)\( \Rightarrow \,\,{A_1}{A_2} = 2.5 = 10\).
*Phương pháp giải:
Cho elip (E) có phương trình
- Trục lớn của (E) nằm trên Ox:
*Lý thuyết:
1. Định nghĩa elip
Cho hai điểm cố định và và một độ dài không đổi 2a lớn hơn . Elip là tập hợp các điểm M trong mặt phẳng sao cho .
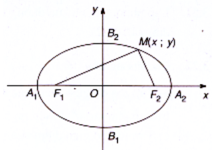
- Hình dạng của elip: Elip có hai trục đối xứng là Ox, Oy và có tâm đối xứng là gốc toạ độ.
2. Các thành phần của Elip
Trong mặt phẳng Oxy
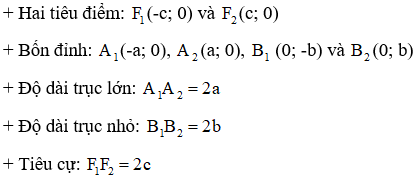
II. Phương trình chính tắc của elip
Cho elip (E) có các tiêu điểm và . Điểm M thuộc elip khi và chỉ khi . Chọn hệ trục tọa độ Oxy, cho (-c; 0) và (c; 0). Khi đó ta có:
M (x; y) . (1) với
Phương trình (1) là phương trình chính tắc của elip.
III. Liên hệ giữa đường tròn và đường elip
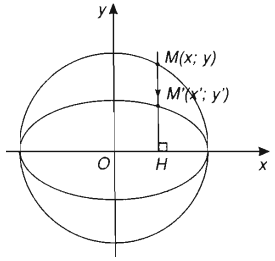
+ Từ hệ thức ta thấy nếu tiêu cự của elip càng nhỏ thì b càng gần bằng a, tức là trục nhỏ của elip càng gần bằng trục lớn. Lúc đó elip có dạng gần như đường tròn
+ Trong mặt phẳng Oxy cho đường tròn (C) có phương trình . Với mỗi điểm M (x; y) thuộc đường tròn ta xét điểm M’(x’; y’) sao cho : với (0 < b < a) thì tập hợp các điểm M’ có tọa độ thỏa mãn phương trình:
là một elip (E). Khi đó ta nói đường tròn (C) được co thành elip (E).
Xem thêm
Phương trình đường elip (Lý thuyết, công thức) các dạng bài tập và cách giải
Đáp án đúng là: B
Lời giải
Gọi phương trình của Elip là \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1,\) có độ dài trục lớn \({A_1}{A_2} = \) 2a.
Xét \(\left( E \right):\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\) \( \Rightarrow \left\{ \begin{array}{l}{a^2} = 25\\{b^2} = 9\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}a = 5\\b = 3\end{array} \right.\,\,\)\( \Rightarrow \,\,{A_1}{A_2} = 2.5 = 10\).
*Phương pháp giải:
Cho elip (E) có phương trình
- Trục lớn của (E) nằm trên Ox:
*Lý thuyết:
1. Định nghĩa elip
Cho hai điểm cố định và và một độ dài không đổi 2a lớn hơn . Elip là tập hợp các điểm M trong mặt phẳng sao cho .

- Hình dạng của elip: Elip có hai trục đối xứng là Ox, Oy và có tâm đối xứng là gốc toạ độ.
2. Các thành phần của Elip
Trong mặt phẳng Oxy

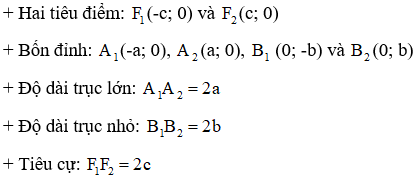
II. Phương trình chính tắc của elip
Cho elip (E) có các tiêu điểm và . Điểm M thuộc elip khi và chỉ khi . Chọn hệ trục tọa độ Oxy, cho (-c; 0) và (c; 0). Khi đó ta có:
M (x; y) . (1) với
Phương trình (1) là phương trình chính tắc của elip.
III. Liên hệ giữa đường tròn và đường elip
+ Từ hệ thức ta thấy nếu tiêu cự của elip càng nhỏ thì b càng gần bằng a, tức là trục nhỏ của elip càng gần bằng trục lớn. Lúc đó elip có dạng gần như đường tròn
+ Trong mặt phẳng Oxy cho đường tròn (C) có phương trình . Với mỗi điểm M (x; y) thuộc đường tròn ta xét điểm M’(x’; y’) sao cho : với (0 < b < a) thì tập hợp các điểm M’ có tọa độ thỏa mãn phương trình:
là một elip (E). Khi đó ta nói đường tròn (C) được co thành elip (E).

Xem thêm
Phương trình đường elip (Lý thuyết, công thức) các dạng bài tập và cách giảiCÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Elip \(\left( E \right):4{x^2} + 16{y^2} = 1\) có độ dài trục lớn bằng:
Elip \(\left( E \right):4{x^2} + 16{y^2} = 1\) có độ dài trục lớn bằng:
Câu 2:
Cho parabol (P) có phương trình chính tắc là \({y^2} = 2px\), với p > 0. Khi đó khẳng định nào sau đây sai?
Cho parabol (P) có phương trình chính tắc là \({y^2} = 2px\), với p > 0. Khi đó khẳng định nào sau đây sai?
Câu 3:
Cho Hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a, b > 0. Khi đó khẳng định nào sau đây sai?
Cho Hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a, b > 0. Khi đó khẳng định nào sau đây sai?
Câu 5:
Elip \(\left( E \right):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\) có độ dài trục bé bằng:
Elip \(\left( E \right):\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{64}} = 1\) có độ dài trục bé bằng:
Câu 7:
Elip \(\left( E \right):\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) có tiêu cự bằng:
Elip \(\left( E \right):\frac{{{x^2}}}{9} + \frac{{{y^2}}}{4} = 1\) có tiêu cự bằng:
Câu 8:
Elip \(\left( E \right):\frac{{{x^2}}}{{16}} + {y^2} = 4\) có tổng độ dài trục lớn và trục bé bằng:
Elip \(\left( E \right):\frac{{{x^2}}}{{16}} + {y^2} = 4\) có tổng độ dài trục lớn và trục bé bằng:
Câu 9:
Elip \(\left( E \right):{x^2} + 5{y^2} = 25\) có độ dài trục lớn bằng:
Elip \(\left( E \right):{x^2} + 5{y^2} = 25\) có độ dài trục lớn bằng:
Câu 10:
Cho elip \[\left( E \right):4{x^2} + 9{y^2} = 36\]. Tìm mệnh đề sai trong các mệnh đề sau:
Cho elip \[\left( E \right):4{x^2} + 9{y^2} = 36\]. Tìm mệnh đề sai trong các mệnh đề sau:
Câu 11:
Cho Hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a, b > 0. Khi đó khẳng định nào sau đây đúng?
Cho Hypebol (H) có phương trình chính tắc là \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\), với a, b > 0. Khi đó khẳng định nào sau đây đúng?
Câu 12:
Đường thẳng nào là đường chuẩn của parabol \({y^2} = \frac{3}{2}x\)
Đường thẳng nào là đường chuẩn của parabol \({y^2} = \frac{3}{2}x\)


