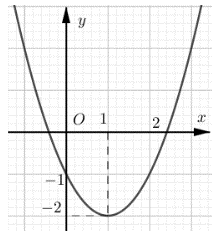
Câu hỏi:
12/07/2024 164
Điểm nào sau đây thuộc đồ thị hàm số y=2x−1x(3x−4)?
A. M(0; 1);
B. N(2;−34);
C. P(43;0);
D. Q(−2;−14).
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: D
Ta đặt f(x)=2x−1x(3x−4).
Biểu thức f(x) có nghĩa khi và chỉ khi x(3x – 4) ≠ 0.
Tức là khi x ≠ 0 và 3x – 4 ≠ 0.
Do đó x ≠ 0 và x≠43.
Vì vậy hàm số có tập xác định là D=R∖{0;43}.
Các điểm M, P có hoành độ lần lượt là 0 và 43 đều không thuộc tập xác định D của hàm số đã cho.
Do đó ta loại phương án A, C.
⦁ Ta xét điểm N(2;−34), ta có hoành độ 2 ∈ D.
Ta có f(2)=2.2−12(3.2−4)=34≠−34.
Do đó điểm N(2;−34) không thuộc đồ thị hàm số y=2x−1x(3x−4).
Vì vậy ta loại phương án B.
⦁ Ta xét điểm Q(−2;−14), ta có –2 ∈ D.
Ta có f(−2)=2.(−2)−1−2[3.(−2)−4]=−14.
Do đó điểm Q(−2;−14) thuộc đồ thị hàm số y=2x−1x(3x−4).
Vậy ta chọn phương án D.
Hướng dẫn giải
Đáp án đúng là: D
Ta đặt f(x)=2x−1x(3x−4).
Biểu thức f(x) có nghĩa khi và chỉ khi x(3x – 4) ≠ 0.
Tức là khi x ≠ 0 và 3x – 4 ≠ 0.
Do đó x ≠ 0 và x≠43.
Vì vậy hàm số có tập xác định là D=R∖{0;43}.
Các điểm M, P có hoành độ lần lượt là 0 và 43 đều không thuộc tập xác định D của hàm số đã cho.
Do đó ta loại phương án A, C.
⦁ Ta xét điểm N(2;−34), ta có hoành độ 2 ∈ D.
Ta có f(2)=2.2−12(3.2−4)=34≠−34.
Do đó điểm N(2;−34) không thuộc đồ thị hàm số y=2x−1x(3x−4).
Vì vậy ta loại phương án B.
⦁ Ta xét điểm Q(−2;−14), ta có –2 ∈ D.
Ta có f(−2)=2.(−2)−1−2[3.(−2)−4]=−14.
Do đó điểm Q(−2;−14) thuộc đồ thị hàm số y=2x−1x(3x−4).
Vậy ta chọn phương án D.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = ax2 + bx + c có đồ thị như hình vẽ:
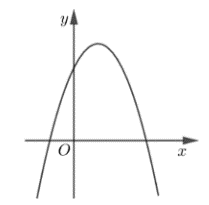
Mệnh đề nào dưới đây đúng?
Cho hàm số y = ax2 + bx + c có đồ thị như hình vẽ:

Mệnh đề nào dưới đây đúng?
Câu 5:
Hàm số y = –x2 + 2x + 3 có đồ thị là hình nào trong các hình sau?
Câu 6:
Xác định các hệ số m, n để parabol (P): y = mx2 + 4x – n (m ≠ 0) có đỉnh S(–1; –5).
Câu 7:
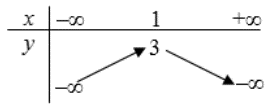
Cho hàm số y = f(x) xác định trên đọa [–3; 3] và có đồ thị được biểu diễn như hình bên:
Khẳng định nào sau đây đúng?
Câu 9:
Cho hàm số y = 2x2 – 4x + 3 có đồ thị là parabol (P). Mệnh đề nào sau đây sai?
Câu 11:
Cho hàm số y=h(x)={−2(x2+1),khix≤14√x−1,khix>1. Khi đó h(√22) bằng:
Câu 12:
Cho hàm số f(x)={−2x+1,khix≤−3x+72,khix>−3. Nếu f(x0) = 5 thì x0 bằng: