Câu hỏi:
21/07/2024 1,919
Có bao nhiêu giá trị nguyên của m để bất phương trình x2 + 3mx2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ.
Có bao nhiêu giá trị nguyên của m để bất phương trình x2 + 3mx2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ.
A. 1;
A. 1;
B. 4;
B. 4;
C. 6;
C. 6;
D. 5.
D. 5.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Ta có x2 + 3mx2 + 4mx + 4 ≥ 0
\( \Leftrightarrow \) (1 + 3m)x2 + 4mx + 4 ≥ 0
Với 1 + 3m = 0 thì m = \( - \frac{1}{3}\) thì bất phương trình trở thành \( - \frac{4}{3}\)x + 4 ≥ 0 ⇔ x ≤ 3. Vậy m = \( - \frac{1}{3}\) không thỏa mãn.
Với 1 + 3m ≠ 0 thì m ≠ \( - \frac{1}{3}\)
Để bất phương trình (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ thì
\( \Leftrightarrow \left\{ \begin{array}{l}1 + 3m > 0\\\Delta ' = 4{m^2} - 12m - 4 \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > - \frac{1}{3}\\4{m^2} - 12m - 4 \le 0\end{array} \right.\)
Xét f(m) = 4m2 – 12m – 4 có ∆ = 208 > 0, hai nghiệm phân biệt là x = \(\frac{{3 - \sqrt {13} }}{2}\) ; x = \(\frac{{3 + \sqrt {13} }}{2}\) và a = 4 > 0
Ta có bảng xét dấu
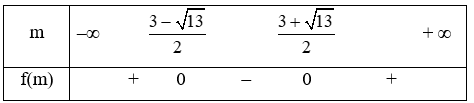
Từ bảng xét dấu ta có để f(m) ≤ 0 thì \(\frac{{3 - \sqrt {13} }}{2}\)≤ m ≤ \(\frac{{3 + \sqrt {13} }}{2}\)
Kết hợp với điều kiện của m để (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ thì \(\frac{{3 - \sqrt {13} }}{2}\)≤ m ≤ \(\frac{{3 + \sqrt {13} }}{2}\)
Vậy có 4 giá trị nguyên của m để bất phương trình (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ.
Đáp án đúng là: B
Ta có x2 + 3mx2 + 4mx + 4 ≥ 0
\( \Leftrightarrow \) (1 + 3m)x2 + 4mx + 4 ≥ 0
Với 1 + 3m = 0 thì m = \( - \frac{1}{3}\) thì bất phương trình trở thành \( - \frac{4}{3}\)x + 4 ≥ 0 ⇔ x ≤ 3. Vậy m = \( - \frac{1}{3}\) không thỏa mãn.
Với 1 + 3m ≠ 0 thì m ≠ \( - \frac{1}{3}\)
Để bất phương trình (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ thì
\( \Leftrightarrow \left\{ \begin{array}{l}1 + 3m > 0\\\Delta ' = 4{m^2} - 12m - 4 \le 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m > - \frac{1}{3}\\4{m^2} - 12m - 4 \le 0\end{array} \right.\)
Xét f(m) = 4m2 – 12m – 4 có ∆ = 208 > 0, hai nghiệm phân biệt là x = \(\frac{{3 - \sqrt {13} }}{2}\) ; x = \(\frac{{3 + \sqrt {13} }}{2}\) và a = 4 > 0
Ta có bảng xét dấu

Từ bảng xét dấu ta có để f(m) ≤ 0 thì \(\frac{{3 - \sqrt {13} }}{2}\)≤ m ≤ \(\frac{{3 + \sqrt {13} }}{2}\)
Kết hợp với điều kiện của m để (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ thì \(\frac{{3 - \sqrt {13} }}{2}\)≤ m ≤ \(\frac{{3 + \sqrt {13} }}{2}\)
Vậy có 4 giá trị nguyên của m để bất phương trình (1 + 3m)x2 + 4mx + 4 ≥ 0 với mọi x \( \in \) ℝ.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Xác định m để bất phương trình x2 + 2(m – 2)x + 2m – 1 > 0 có nghiệm với mọi x \( \in \) ℝ.
Xác định m để bất phương trình x2 + 2(m – 2)x + 2m – 1 > 0 có nghiệm với mọi x \( \in \) ℝ.
Câu 2:
Biểu thức f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương khi và chỉ khi:
Biểu thức f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương khi và chỉ khi:
Câu 3:
Tích các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
Tích các nghiệm của phương trình \[{x^2} - 2x + 3\sqrt {{x^2} - 2x - 3} = 7\] là:
Câu 4:
Với x thuộc tập hợp nào dưới đây thì f(x) = 2x2 – 7x – 15 không âm?
Với x thuộc tập hợp nào dưới đây thì f(x) = 2x2 – 7x – 15 không âm?
Câu 5:
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) ≤ 0 với \[\forall x \in \mathbb{R}\].
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) ≤ 0 với \[\forall x \in \mathbb{R}\].
Câu 6:
Số nghiệm của phương trình 4x2 – 12x + 5\(\sqrt {4{x^2} - 12x} \) = 0
Số nghiệm của phương trình 4x2 – 12x + 5\(\sqrt {4{x^2} - 12x} \) = 0
Câu 7:
Cho f(x) = x2 – 4. Tìm khẳng định sai trong các khẳng định sau đây
Cho f(x) = x2 – 4. Tìm khẳng định sai trong các khẳng định sau đây
Câu 9:
Tích các nghiệm của phương trình x2 + 2\(\sqrt {{x^2} - 3x + 11} \) = 3x + 4 là
Tích các nghiệm của phương trình x2 + 2\(\sqrt {{x^2} - 3x + 11} \) = 3x + 4 là
Câu 10:
Gọi x là nghiệm của phương trình
\(\sqrt {3x - 2} + \sqrt {x - 1} = 4x - 9 + 2\sqrt {3{x^2} - 5x + 2} \)
Tính giá trị của biểu thức A = x2 – 3x + 15
Gọi x là nghiệm của phương trình
\(\sqrt {3x - 2} + \sqrt {x - 1} = 4x - 9 + 2\sqrt {3{x^2} - 5x + 2} \)
Tính giá trị của biểu thức A = x2 – 3x + 15
Câu 13:
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] thuộc khoảng nào trong các khoảng sau
Nghiệm của phương trình \[\sqrt {x - 2} + \sqrt {x + 3} = 5\] thuộc khoảng nào trong các khoảng sau
Câu 14:
Tổng các nghiệm của phương trình \(\sqrt {x + 3} + \sqrt {6 - x} = 3 + \sqrt {(x + 3)(6 - x)} \) (*) là
Tổng các nghiệm của phương trình \(\sqrt {x + 3} + \sqrt {6 - x} = 3 + \sqrt {(x + 3)(6 - x)} \) (*) là


