Câu hỏi:
21/07/2024 212
Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính .
Cho tam giác ABC đều cạnh a, H là trung điểm của BC. Tính .
A.
B.
C.
D.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D.
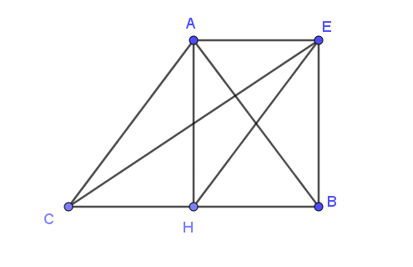
Ta có:
Dựng hình bình hành CAEH.
Do tam giác ABC đều nên AH vừa là trung tuyến vừa là đường cao.
Do đó, AH vuông góc với BC .
Mà AE // CH (do CAEH là hình bình hành)
Do đó, AH vuông góc với AE .
Vậy AEBH là hình chữ nhật.
Ta có: CH = BH = .
Xét tam giác CHA vuông tại H
Áp dụng định lý Pythagore ta có:
AC2 = AH2 + CH2 ⇔ AH2 = AC2 – CH2 = ⇒ .
⇒ (do AEBH là hình chữ nhật)
Xét tam giác CBE vuông tại B
Áp dụng định lý Pythagore ta có:
CE2 = BC2 + BE2 = ⇒ .
Theo quy tắc hình bình hành: .
.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình vuông ABCD cạnh bằng 2, có tâm O. Khi đó ta tính được Tính giá trị biểu thức A = 2a2 – 5a.
Cho hình vuông ABCD cạnh bằng 2, có tâm O. Khi đó ta tính được Tính giá trị biểu thức A = 2a2 – 5a.
Câu 4:
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Độ dài của vectơ bằng:
Cho tam giác ABC vuông tại A có AB = 3, AC = 4. Độ dài của vectơ bằng:
Câu 5:
Cho hình vuông ABCD cạnh 2, tâm O. Tính độ dài của vectơ với . Khẳng định nào sau đây là đúng?
Cho hình vuông ABCD cạnh 2, tâm O. Tính độ dài của vectơ với . Khẳng định nào sau đây là đúng?


