Câu hỏi:
22/07/2024 165
Cho hình thoi ABCD cạnh 5 và ^ABC=60o. Tính: |2→AB−2→AD|.
Cho hình thoi ABCD cạnh 5 và ^ABC=60o. Tính: |2→AB−2→AD|.
A. 10;
B. 5√32;
C. 5;
D. 10√3.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D.
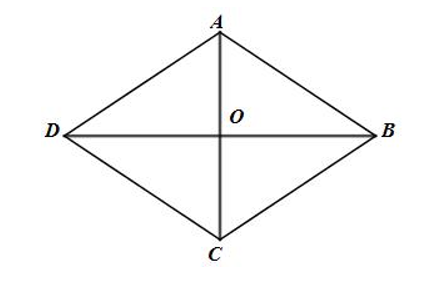
Ta có: 2→AB−2→AD=2(→AB−→AD)=2→DB (hiệu hai vectơ).
Gọi O là giao hai đường chéo của hình thoi, khi đó O là trung điểm của AC và BD. Hơn nữa hai đường chéo này vuông góc với nhau tại O.
Xét tam giác ABC có:
^ABC=60o
AB = BC (do ABCD là hình thoi)
Do đó, tam giác ABC là tam giác đều
⇒ AC = AB = BC = 5
⇒AO=12AC=12.5=2,5
Xét tam giác AOB vuông tại O, theo định lí Pytahgore ta có:
AB2=AO2+BO2⇒BO2=AB2−AO2=52−2,52=18,75
⇒BO=5√32
⇒BD=2BO=2.5√32=5√3
Vậy |2→AB−2→AD|=|2→DB|=|2||→DB|=2DB=2.5√3=10√3.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ 12→DB.
Cho hình chữ nhật ABCD tâm O có AB = 4, AD = 3. Tính độ dài vectơ 12→DB.
Câu 3:
Cho tam giác đều ABC cạnh a. Điểm M là trung điểm BC. Tính: |12→CB+→MA|.
Cho tam giác đều ABC cạnh a. Điểm M là trung điểm BC. Tính: |12→CB+→MA|.
Câu 4:
Cho tam giác ABC đều cạnh 4a. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Tính: |12→BA−12→BC|.
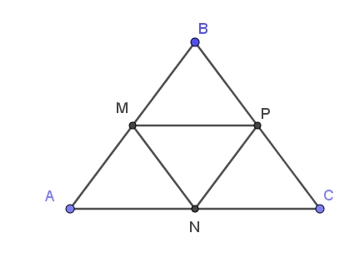
Cho tam giác ABC đều cạnh 4a. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Tính: |12→BA−12→BC|.

Câu 8:
Cho hình vuông ABCD tâm O cạnh 2a. Vectơ tổng 2→AB+2→DC có độ dài là
Cho hình vuông ABCD tâm O cạnh 2a. Vectơ tổng 2→AB+2→DC có độ dài là


