Câu hỏi:
22/11/2024 5,106
Cho hàm số y = f(x). Biết f(x + 2) = x2 – 3x + 2 thì f(x) bằng:
Cho hàm số y = f(x). Biết f(x + 2) = x2 – 3x + 2 thì f(x) bằng:
A. y = f(x) = x2 + 7x – 12;
A. y = f(x) = x2 + 7x – 12;
B. y = f(x) = x2 – 7x – 12;
B. y = f(x) = x2 – 7x – 12;
C. y = f(x) = x2 + 7x + 12;
C. y = f(x) = x2 + 7x + 12;
D. y = f(x) = x2 – 7x + 12.
D. y = f(x) = x2 – 7x + 12.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng: D
* Lời giải:
Đặt x + 2 = t ⇔ x = t – 2
Khi đó, ta có f(t) = (t – 2)2 – 3(t – 2) + 2 = t2 – 7t + 12
Vậy f(x) = x2 – 7x + 12.
* Phương pháp giải:
- Biến đổi hàm f(x+2) về hàm số f(x) bằng cách: Đặt x+2 = t; khi đó ta sẽ tìm ra được hàm f(t)
* Lý thuyết và các dạng bài về hàm số bậc hai:
Khái niệm hàm số bậc hai
Hàm số bậc hai là hàm số cho bởi công thức y = ax2 + bx + c, trong đó x là biến số, a, b, c là các hằng số và a ≠ 0.
Tập xác định của hàm số bậc hai là ℝ.
Nhận xét : Hàm số y = ax2 (a ≠ 0) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với b = c = 0.
Đồ thị của hàm số bậc hai
- Đồ thị của hàm số bậc hai là một parabol.
- Đồ thị hàm số y = ax2 + bx + c (a ≠ 0) là một đường parabol có đỉnh là điểm , có trục đối xứng là đường thẳng . Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0.
- Để vẽ đường parabol y = ax2 + bx + c ta tiến hành theo các bước sau :
1. Xác định tọa độ đỉnh ;
2. Vẽ trục đối xứng ;
3. Xác định tọa độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol ;
4. Vẽ parabol.
Nhận xét : Từ đồ thị hàm số y = ax2 + bx + c (a ≠ 0), ta suy ra tính chất của hàm số y = ax2 + bx + c (a ≠ 0):
|
Với a > 0 |
Với a < 0 |
|
Hàm số nghịch biến trên khoảng ; Hàm số đồng biến trên khoảng ; là giá trị nhỏ nhất của hàm số. |
Hàm số đồng biến trên khoảng ; Hàm số nghịch biến trên khoảng ; là giá trị lớn nhất của hàm số.
|
Xem thêm các bài viết liên quan hay, chi tiết:
Lý thuyết Hàm số bậc hai - Toán 10 Kết nối tri thức
Giải Toán 10 Bài 16 (Kết nối tri thức): Hàm số bậc hai
Thi Online Trắc nghiệm Toán 10 Bài 16. Hàm số bậc hai có đáp án
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
Câu 4:
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
Câu 5:
Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng −14. Tính tích P = a.b.
Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng −14. Tính tích P = a.b.
Câu 6:
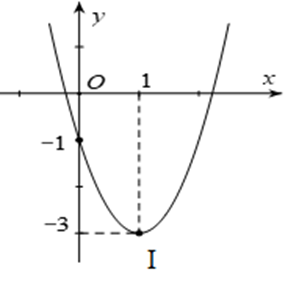
Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?
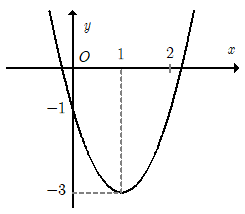
Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?

Câu 7:
Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
Câu 8:
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
Câu 9:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
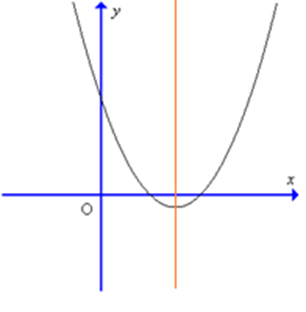
Kết luận nào sau đây đúng về hệ số a, b:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:

Kết luận nào sau đây đúng về hệ số a, b:
Câu 10:
Cho hàm số y = f(x) có đồ thị như hình sau:
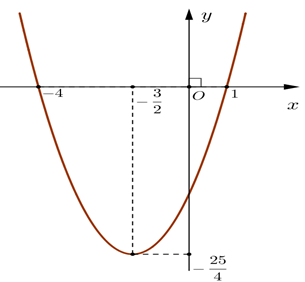
Hàm số đồng biến trên khoảng
Cho hàm số y = f(x) có đồ thị như hình sau:

Hàm số đồng biến trên khoảng
Câu 12:
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?