Câu hỏi:
17/07/2024 1,079
Tọa độ đỉnh I của hàm số y = – 3x2 + 4x – 1
Tọa độ đỉnh I của hàm số y = – 3x2 + 4x – 1
A. \[{\rm{I}}\left( {--\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\];
A. \[{\rm{I}}\left( {--\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\];
B. \[{\rm{I}}\left( {\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\];
B. \[{\rm{I}}\left( {\frac{{\rm{2}}}{{\rm{3}}}{\rm{;}}\frac{{\rm{1}}}{{\rm{3}}}} \right)\];
C. \[{\rm{I}}\left( {\frac{{\rm{4}}}{{\rm{3}}}{\rm{;}}--{\rm{1}}} \right)\];
C. \[{\rm{I}}\left( {\frac{{\rm{4}}}{{\rm{3}}}{\rm{;}}--{\rm{1}}} \right)\];
D. \[{\rm{I}}\left( {\frac{2}{{\rm{3}}}{\rm{;}}\frac{4}{{\rm{3}}}} \right)\].
D. \[{\rm{I}}\left( {\frac{2}{{\rm{3}}}{\rm{;}}\frac{4}{{\rm{3}}}} \right)\].
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Tọa độ đỉnh \[{\rm{I}}\left( {--\frac{{\rm{b}}}{{{\rm{2a}}}}{\rm{;}}--\frac{{\rm{\Delta }}}{{{\rm{4a}}}}} \right)\]
Ta có giá trị \( - \frac{b}{{2a}} = - \frac{4}{{2.( - 3)}} = \frac{2}{3}\),
giá trị \( - \frac{\Delta }{{4a}} = - \frac{{{4^2} - 4.( - 3).( - 1)}}{{4.( - 3)}} = \frac{1}{3}\).
Vậy toạ độ đỉnh I\(\left( {\frac{2}{3};\frac{1}{3}} \right)\)
Đáp án đúng là: B
Tọa độ đỉnh \[{\rm{I}}\left( {--\frac{{\rm{b}}}{{{\rm{2a}}}}{\rm{;}}--\frac{{\rm{\Delta }}}{{{\rm{4a}}}}} \right)\]
Ta có giá trị \( - \frac{b}{{2a}} = - \frac{4}{{2.( - 3)}} = \frac{2}{3}\),
giá trị \( - \frac{\Delta }{{4a}} = - \frac{{{4^2} - 4.( - 3).( - 1)}}{{4.( - 3)}} = \frac{1}{3}\).
Vậy toạ độ đỉnh I\(\left( {\frac{2}{3};\frac{1}{3}} \right)\)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hàm số y = f(x). Biết f(x + 2) = x2 – 3x + 2 thì f(x) bằng:
Cho hàm số y = f(x). Biết f(x + 2) = x2 – 3x + 2 thì f(x) bằng:
Câu 2:
Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
Cho parabol y = ax2 + bx – 3. Xác định hệ số a, b biết parabol có đỉnh
I(– 1; – 5)
Câu 4:
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
Biết rằng hàm số y = ax2 + bx + c (a ≠ 0) đạt cực đại bằng 3 tại x = 2 và có đồ thị hàm số đi qua điểm A(0; – 1). Tính tổng S = a + b + c.
Câu 5:
Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?
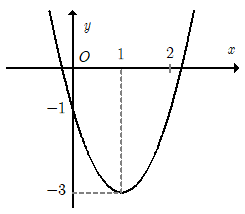
Cho hàm số y = ax2 + bx + c có đồ thị như hình dưới đây. Hàm số đó là hàm số nào?

Câu 6:
Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng \( - \frac{1}{4}\). Tính tích P = a.b.
Biết rằng P: y = ax2 + bx + 2 (a > 1) đi qua điểm M(–1; 6) và có tung độ đỉnh bằng \( - \frac{1}{4}\). Tính tích P = a.b.
Câu 7:
Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
Cho hàm số y = 2x2 – 4x – 1. Kết luận nào đúng trong các kết luận sau
Câu 8:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:
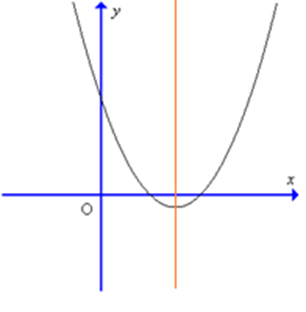
Kết luận nào sau đây đúng về hệ số a, b:
Cho hàm số y = ax2 + bx + c có đồ thị như hình sau:

Kết luận nào sau đây đúng về hệ số a, b:
Câu 9:
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
Parabol y = ax2 + bx + c đạt giá trị nhỏ nhất bằng 4 tại x = – 2 và đi qua
A(0; 6) có phương trình là
Câu 10:
Cho hàm số y = f(x) có đồ thị như hình sau:
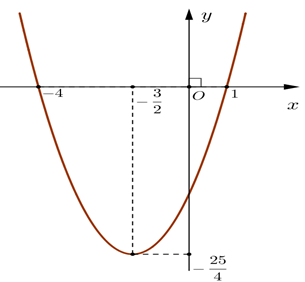
Hàm số đồng biến trên khoảng
Cho hàm số y = f(x) có đồ thị như hình sau:

Hàm số đồng biến trên khoảng
Câu 12:
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?
Đồ thị hàm số y = 4x2 – 3x – 1 có dạng nào trong các dạng sau đây?