Câu hỏi:
16/11/2024 8,777
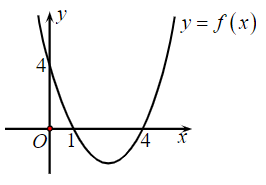
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ:
Đặt ∆ = b2 – 4ac. Tìm dấu của a và ∆.
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình vẽ:

Đặt ∆ = b2 – 4ac. Tìm dấu của a và ∆.
A. a > 0, ∆ > 0;
B. a < 0, ∆ > 0;
C. a > 0, ∆ = 0;
D. a < 0, ∆ = 0.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
Lời giải
Quan sát đồ thị, ta thấy parabol có bề lõm quay lên trên nên a > 0.
Lại có đồ thị cắt trục Ox tại hai điểm phân biệt (cụ thể là tại x = 1 và x = 4) nên phương trình ax2 + bx + c = 0 có hai nghiệm x1, x2.
Do đó ∆ > 0.
Vậy a > 0, ∆ > 0.
Do đó ta chọn phương án A.
*Phương pháp giải:
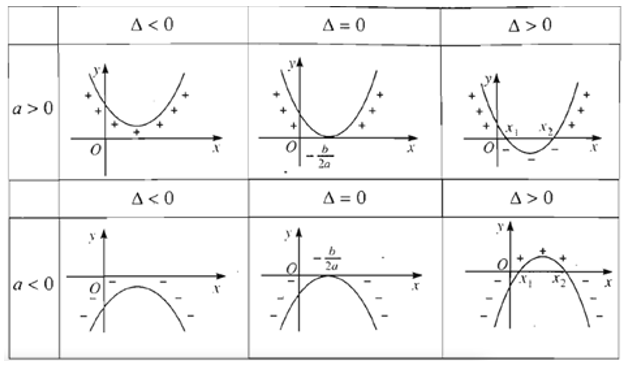
Dựa vào định lí về dấu của tam thức bậc hai có minh họa hình học sau
*Lý thuyết:
Tam thức bậc hai đối với x là biểu thức có dạng
f(x) = ax2 + bx + c,
trong đó a, b, c là những hệ số, a ≠ 0.
2. Dấu của tam thức bậc hai
Người ta đã chứng minh được định lí về dấu tam thức bậc hai sau đây
Định lý
Cho f(x) = ax2 + bx + c (a ≠ 0), Δ = b2 – 4ac.
Nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a, với mọi x ∈ R.
Nếu Δ = 0 thì f(x) luôn cùng dấu với hệ số a, trừ khi x = -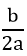
Nếu Δ > 0 thì f(x) luôn cùng dấu với hệ số a khi x < x1 hoặc x > x2, trái dấu với hệ số a khi x1 < x < x2 trong đó x1, x2 (x1 < x2) là hai nghiệm của f(x).
Chú ý
Trong định lí trên, có thể thay biệt thức Δ = b2 – 4ac bằng biệt thức thu gọn Δ’ = (b’)2 – ac
Minh họa hình học
Định lí về dấu của tam thức bậc hai có minh họa hình học sau
Xem thêm
Lý thuyết Dấu của tam thức bậc hai – Toán 10 Chân trời sáng tạo
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trục đối xứng của parabol y = –x2 + 5x + 3 là đường thẳng có phương trình:
Câu 2:
Cho hàm số y = f(x) = ax2 + bx + c có đồ thị như hình bên:
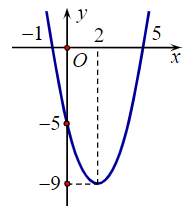
Trục đối xứng của đồ thị hàm số trên là đường thẳng: